что относится к реальным газам
Реальные газы
Реальный газ — газ, который не описывается уравнением состояния идеального газа Менделеева—Клапейрона.
где p — давление; T — температура; Zr = Zr (p,T) — коэффициент сжимаемости газа; М — масса; R — газовая постоянная.
Физика реального газа
Чтобы подробнее установить условия, когда газ может превратиться в жидкость и наоборот, простых наблюдений за испарением или кипением жидкости недостаточно. Надо внимательно проследить за изменением давления и объема реального газа при разных температурах.
Медленно будем сжимать газ в сосуде с поршнем, например сернистый ( SO2 ). Сжимая его, мы выполняем над ним работу, вследствие чего внутренняя энергия газа увеличится. Когда мы хотим, чтобы процесс происходил при постоянной температуре, то сжимать газ надо очень медленно, чтобы теплота успевала переходить от газа в окружающую среду.
Выполняя этот опыт, можно заметить, что сначала при большом объеме давление с уменьшением объема увеличивается согласно закону Бойля—Мариотта. В конце концов, начиная с какого-то значения, давление не будет изменяться, несмотря на уменьшение объема. На стенках цилиндра и поршня образуются прозрачные капли. Это означает, что газ начал конденсироваться, то есть переходить в жидкое состояние.
Продолжая сжимать содержимое цилиндра, мы будем увеличивать массу жидкости под поршнем и, соответственно, будем уменьшать массу газа. Давление, которое показывает манометр, будет оставаться постоянным до тех пор, пока все пространство под поршнем не заполнит жидкость. Жидкости мало сжимаемы. Поэтому дальше, даже при незначительном уменьшении объема, давление быстро будет возрастать.
Поскольку весь процесс происходит при постоянной температуре Т, кривую, что изображает зависимость давления р от объема V, называют изотермой. При объеме V1 начинается конденсация газа, а при объеме V2 она заканчивается. Если V > V1 то вещество будет в газообразном состоянии, а при V Уравнения состояния реального газа
Наиболее часто используются следующие уравнения состояния реального газа:
Полезное
Смотреть что такое «Реальные газы» в других словарях:
неконденсирующиеся газы — 3.11 неконденсирующиеся газы: Это идеальные газы и разряженные реальные газы, при температурах, далеких от температуры конденсации. Источник … Словарь-справочник терминов нормативно-технической документации
идеальный газ — идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальному газу близки разреженные реальные газы при температурах, далёких от температуры их конденсации. Зависимость… … Энциклопедический словарь
ТЕРМОДИНАМИКА — раздел прикладной физики или теоретической теплотехники, в котором исследуется превращение движения в теплоту и наоборот. В термодинамике рассматриваются не только вопросы распространения теплоты, но и физические и химические изменения, связанные … Энциклопедия Кольера
СТО 70238424.27.100.064-2009: Геотермальные электростанции (ГеоТЭС). Охрана труда (правила безопасности) при эксплуатации и техническом обслуживании. Нормы и требования — Терминология СТО 70238424.27.100.064 2009: Геотермальные электростанции (ГеоТЭС). Охрана труда (правила безопасности) при эксплуатации и техническом обслуживании. Нормы и требования: 3.1 безопасность: Отсутствие допустимого риска, связанного с… … Словарь-справочник терминов нормативно-технической документации
ИДЕАЛЬНЫЙ ГАЗ — теор. модель газа, в к рой не учитывается вз ствие ч ц газа (ср. кинетич. энергия ч ц много больше энергий их вз ствия). Различают классич. и квант. И. г. Св ва классического И. г. описываются законами классич. физики Клапейрона уравнением и его… … Физическая энциклопедия
Внутренняя энергия — энергия тела, зависящая только от его внутреннего состояния. Понятие В. э. объединяет все виды энергии тела, за исключением энергии его движения как целого и потенциальной энергии, которой тело может обладать, если оно находится в поле… … Большая советская энциклопедия
Идеальный газ — теоретическая модель газа, в которой пренебрегается взаимодействием частиц газа (средняя кинетическая энергия частиц много больше энергии их взаимодействия). Различают классический И. г. (его свойства описываются законами… … Большая советская энциклопедия
ГЕЙЛЬБРОННЕРА СИМПТОМ — (Heilbron ner), состоит в появлении при органических параличах расширения и уплотнения мягких тканей бедра при лежании на спине и на твердой подстилке и является хорошим пособием при диференциальном диагнозе органических параличей от истерических … Большая медицинская энциклопедия
ИДЕАЛЬНЫЙ ГАЗ — идеализированная модель газа; в идеальном газе силы взаимодействия между частицами (атомами, молекулами) пренебрежимо малы. К идеальному газу близки разреженные реальные газы при температурах, далеких от температуры их конденсации. Зависимость… … Большой Энциклопедический словарь
ВНУТРЕННЯЯ ЭНЕРГИЯ — энергия физ. системы, зависящая от её внутр. состояния. В. э. включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т. д.) и энергию вз ствия этих ч ц. Кинетич. энергия движения системы как целого и … Физическая энциклопедия
Реальный газ, основные понятия и формулы
Реальный газ – это такой газ, который не является идеальным газом.
Описание идеального и реального газа
Идеальный газ – математическая модель газа, которая описывается уравнением состояния идеального газа Клапейрона — Менделеева. Данное уравнение имеет вид:
Уравнение состояния идеального газа Клапейрона — Менделеева
Иначе данную формулу можно записать в следующем виде:
Уравнение состояния идеального газа Клапейрона — Менделеева
Где m – масса, M – молярная масса, а V — объем
В отличие от идеального газа, молекулы реального газа взаимодействуют между собой, а также занимают определенный объем. По этой причине реальный газ описывается так называемым обобщенным уравнением Менделеева — Клапейрона:
Обобщенное уравнение Менделеева — Клапейрона
Как видно – здесь возникает Zr – коэффициент сжимаемости газа, который зависит от температуры и давления. Именно данный коэффициент определяет отклонение термодинамических свойств реальных газов от свойств идеальных.
Z – коэффициент сжимаемости газа
Здесь V – молярный объем. Для идеального газа коэффициент сжимаемости газа равен единице.
Свойства реального газа заметно различны со свойствами идеального в случае, когда температура газа достигает критической точки, либо имеют место высокое давление или низкие температуры. Данные различия имеют большое значение в точных расчетах, например, в гиперзвуковой аэродинамике.
Разница между идеальным и реальным газом
Исследователи выделяют модели газа идеального и реального. В чем их специфика?
Что представляет собой реальный газ?
Под реальным газом, в свою очередь, понимается вещество, которое не может быть описано уравнением Клапейрона — Менделеева. Так, молекулы, присутствующие в нем, взаимодействуют друг с другом, формируют некоторый объем.
Нужно отметить, что во многих случаях характеристики потенциальной энергии, формирующейся в ходе взаимодействия молекул реального газа, существенно ниже кинетической энергии.
Вследствие чего соответствующие газы по своим свойствам приближаются к тем, что характеризуют идеальный газ.
Заметные различия между рассматриваемыми веществами начинают появляться, как правило, при повышении давления и снижении температуры.
Сравнение
Главное отличие идеального газа от реального заключается в том, что в модели первого вещества практически не учитывается объем молекул, а также энергия их взаимодействия. В реальном газе соответствующие показатели учитываются. Вместе с тем при невысоком давлении и большой температуре реальный газ по своим свойствам близок к идеальному.
Определив, в чем разница между идеальным и реальным газом, зафиксируем выводы в таблице.
Таблица
| Идеальный газ | Реальный газ |
| Что общего между ними? | |
| При определенных условиях реальный газ может быть приближен по свойствам к идеальному | |
| В чем разница между ними? | |
| Модель описания вещества не учитывает объем его молекул, а также энергию их взаимодействия друг с другом | Модель описания вещества учитывает объем его молекул и силу их взаимодействия |
Реальный газ, основные понятия и формулы
Уравнение Менделеева-Клапейрона описывает параметры состояния разреженных газов (находящихся при не слишком больших давлениях и при достаточно высоких температурах). При обычных условиях (т.е. при комнатной температуре и атмосферном давлении) это уравнение применимо ко многим газам (например, таким как азот и кислород).
Наиболее близки по своим свойствам к идеальному газу гелий и водород. При низких температурах и высоких давлениях поведение газа начинает существенно отличаться от поведения идеального газа.
С повышением плотности газа процессы столкновений играют все большую роль, поэтому размерами молекул и их взаимодействием пренебрегать уже нельзя.
Взаимодействие между молекулами реального газа носит сложный характер, поэтому получить уравнение состояния, которое бы количественно правильно описывало поведение реального газа во всей области возможных изменений его температуры и плотности, не представляется возможным. Можно, однако, записать приближенное уравнение, которое учитывает основные качественные особенности взаимодействия молекул.
Уравнение Ван-дер-Ваальса
Поправка учитывает быстро возрастающие на малых расстояниях силы отталкивания: молекулы как бы занимают определенный объем, меньше которого газ не может быть сжат. Таким образом, поправка к объему характеризует ту часть объема, которая недоступна для движения молекул и равна нескольким суммарным объемам всех молекул, содержащихся в газе.
называют внутренним молекулярным давлением. Эта поправка учитывает притяжение молекул, следствием которого является уменьшение давления газа. Молекулы идеального газа, сталкиваясь со стенками сосуда, оказывают на него давление.
При учете притяжения на каждую подлетевшую к стенке молекулу действует сила, «отталкивающая» ее от стенки обратно в объем – сила притяжения молекул объема.
Значенияпостоянных Ван-дер-Ваальса a и b зависят от природы газа, но не зависят от температуры, Константа (параметр) a характеризует взаимодействие между молекулами на больших расстояниях – дальнодействие сил, параметр b характеризует взаимодействии на малых расстояниях – близкодействие сил взаимодействия.
Примеры решения задач
ПОИСК
Формульные единицы — это реально существующие частицы, представляющие собой электроны, атомы, молекулы, ионы, условные молекулы кристаллических веществ и полимеров и др. Для характеристики числа чгигтиц вводится понятие количества вещества. Количество вещества В [c.
21] Из самого определения понятия летучести следует, что эта функция не может быть вычислена без помощи экспериментальных данных. Рассмотрим один из возможных способов определения летучести.
Чтобы воспользоваться им, необходимо опытным путем найти изотермическую зависимость между Р и V интересующего нас газа при заданной температуре. По результатам наблюдения строят график (рис. 24, кривая /). По уравнению PV — RT строят изотерму идеального газа для той же температуры (кривая И).
Изотерма // непременно ляжет правее изотермы I, ибо объем реального газа меньше объема идеального газа при той же температуре вследствие межмоле-кулярныХ сил притяжения, действующих в реальном газе. На рис. 24 отмечено давление Р, при котором должна быть [c.
Таким образом, летучесть / — величина, не имеющая определенного физического смысла. Будучи подставленной в уравнение, выведенное для идеального газа, летучесть делает его пригодным и для реального газа. Иногда летучесть называют исправленным давлением, однако этот термин, отражая формально прием, не передает вполне реального содержания понятия. [c.159]
Изложенные выше понятия и определения, связанные с равновесной термодинамической гибкостью, относятся к полимерным цепям, кон-формационные свойства которых определяются только взаимодействиями ближнего порядка.
В реальных цепях в растворе (даже при бесконечном разбавлении) существуют объемные взаимодействия между удаленными по цепи, но случайно сблизившимися в пространстве звеньями одной и той же цепочки.
Эти взаимодействия, подобные взаимодействиям частиц в реальном газе, включают [c.23]
Так же как реальные газы при определенных температурах и давлениях приближаются к идеальному газу, реальные растворы при определенных условиях разбавления приближаются к идеальному раствору. Идеальным называется газ, молекулы которого имеют пренебрежимо малый объем и не взаимодействуют друг с другом.
Очевидно, что для определения идеального раствора эти критерии использовать нельзя, так как молекулы жидкости должны обладать ощутимым относительным объемом и притягивать друг друга, для того чтобы жидкость существовала.
Идеальным является такой раствор, в котором свойства, присущие растворителю и растворенному веществу, не меняются из-за присутствия новых соседей, если не считать возможных изменений этих свойств при разбавлении. Никаких новых сил при этом не возникает, и никакие старые силы не исчезают.
Стремление к улетучиванию для молекул растворителя (так же как и растворенного вещества, если оно обладает летучестью) уменьшается только в той мере, в которой наличие молекул другого компонента пространственно затрудняет или вообще делает невозможным уход молекул растворителя из раствора.
В случае идеальных растворов такие свойства, как объем, являются аддитивными, а температура при смешивании не изменяется. Таким образом, если наш раствор состоит из двух компонентов Л и В, то силы взаимодействия между всеми молекулами будут такими же, как и силы взаимодействия между А VI А, В м В или Л и В. [c.129]
Для изучения процесса переноса энергии излучения используется понятие вектора плотности потока излучения (см. 16.2). Задача о теплообмене излучением считается решенной, если для заданной системы, заполненной излучающей, поглощающей и рассеивающей средой, найдено поле вектора Цд. Если поглощательная способность среды не зависит от частоты V, то такая среда называется серой. На практике чаще встречаются случаи теплообмена излучением, когда излучающую среду серой считать нельзя. В первую очередь это относится к излучению газообразных продуктов сгорания (см. 18.1). Для определения спектральных характеристик излучения реальных газов и твердых частиц применяются различные модели [3, 4, 29, 42]. [c.485]
Система, не обменивающаяся энергией с окружающей средой, называется изолированной системой.
Понятие изолированной системы имеет предельный характер и является такой же удобной рабочей гипотезой, как понятия совершенного газа или идеального раствора, способствующие установлению закономерностей поведения реальных газов и растворов.
Удобнее всего представлять изолированную от воздействия окружающей среды систему, как находящуюся в бесконечном отдалении от источника воздействия или же как отделенную от него оболочкой, обладающей бесконечно большим сопротивлением ко всякого рода внешним воздействиям.
Конечно, в реальных условиях невозможно абсолютно уничтожить взаимодействие системы с окружающей средой, однако в каждом конкретном случае можно сделать его пренебрежимо малым. Это и имеется в виду в определении изолированной системы. [c.9]
При этом будут рассмотрены лишь те вопросы, которые имеют отношение к теории горения. В 2 будут сформулированы общие законы термодинамики, в 3 изложены основные положения статистической механики идеальных газов.
В 4 устанавливаются условия химического равновесия при фазовых переходах и химических реакциях в газах (реальных и идеальных) и в конденсированных фазах (реальных и идеальных). В этом же параграфе указаны методы расчета состава равновесных смесей.
В 5 вводится понятие о теплоте реакции и описаны методы определения этой величины, а также обсуждается расчет адиабатической температуры пламени.
В последнем параграфе ( 6), посвященном конденсированным системам, выводится правило фаз и обсуждаются зависимости давления пара и точки кипения от концентрации, также осмотическое давление и другие вопросы, [c.434]
Практическое применение термодинамических уравнений для расчета фазовых, химических равновесных состояний смесей реальных веществ связано со сложностью определения введенных Льюисом (1901 г.
) понятий летучести и активности веществ и вытекающих из этих понятий, коэффициентов летучестей и активностей, которые позволили сохранить простоту термодинамических уравнений, полученных на основе, гиперболической модели идеального газа, но перенесли основную трудность на определение этих коэффициентов. [c.92]
Значение т) для поршневых компрессоров находится в пределах 0,80— 0,95, что свидетельствует о значительных затратах мощности на механическое трение и привод вспомогательных механизмов. Выше (см. 3, гл.
9) было указано, что для определения совершенства процесса сжатия газов, протекающего в компрессоре, введено понятие изотермного и адиабатного к. п. д., под которым подразумевается отношение мощности идеального компрессора (работающего по изотермному или адиабатному циклу) к мощности реального компрессора.
В этом случае при п Читайте также: Каноническое уравнение, формулы и примеры
Понятие остаточной (Ван-дер-Ваальсовой) связи. При выводе законов для газов обычно делается допущение, что молекулы взаимодействуют друг с другом только при столкновениях. Такое допущение есть идеализация, и сами законы носят название законов идеальных газов.
К реальным газам эти законы применимы лишь в известном приближении и только в определенных условиях (не очень высокие давления и плотности газов). Но даже в этих условиях можно наблюдать отклонения поведения реальных газов от идеальных. Ван-дер-Ваальс (1873 г.
) исследовал эти отклонения и объяснил их тем, что в теории реальных газов следует учитывать взаимодействия между молекулами не только посредством столкновений. Силы такого дополнительного взаимодействия названы Ван-дер-Ваальсовыми, или остаточными силами. [c.
Шкала абсолютно температуры. Идея об абсолютном нуле температуры появилась в результате открытия закона Шарля и Гей-Люссака абсолютным нулем должна быть температура, при которой идеальный газ должен иметь объем, равный нулю при любом конечном давлении. На протягкении ряда лет (вплоть до 1848 г.
) абсолютную шкалу температур определяли как шкалу газового термометра считали, что абсолютная температура пропорциональна объему определенного количества газа при постоянном давлении.
Одпако поскольку не существует реального газа, который был бы достаточно близок к идеальному, позволяющему сконструировать точный газовый термометр, Томсон сформулировал понятие об абсолютной шкале температуры, основываясь на законах термодинамики. Именно эта шкала абсолютной температуры в настоящее время является признанной (она рассмотрена в гл.
П). Шкала водородного газового термометра весьма близка к термодинамической шкале, за исключением области очень низких температур, и поэтому такой термометр широко применяют на практике. [c.244]
Расчетный метод состоит в использовании уравнений состояния реальных газов для определения летучести компонентов смеси в паровой и жидкой фазах и в нахождении константы равновесия как отношения летучести компонента в паровой фазе к его летучести в жидкой фазе. Понятие летучести в практику расчетов парожидкостного равновесия было введено Льюисом. Он предложил сохранить форму уравнения для химического потенциала /-го компонента шеси идеальных газов [c.277]
Классики марксизма-ленинизма подчеркивают, что игнорирование некоторых черт действительности, т. е. создание идеальной картины, рационально и необходимо в процессе познания. Наука строится на основе рассмотрения идеальных картин (идеальных газов, идеальных растворов и т. п.) с постепенным усложнением этих картин путем учета реальных свойств объекта.
Итак, рационально считать молекулы неотличимыми. Однако при этом исчезает рассмотренная выше комбинаторика и вероятности всех состояний оказываются равными (Ц7 =1). Новая комбинаторика возникает не из-за отличимости молекул, а из-за отличимости различных частей фазового пространства.
Уже при рассмотрении третьего принципа термодинамики указывалось, что в отличие от классической механики в квантовой механике имеет месю дискретный набор состояний и энергий. Как мы убедимся далее (часть четвертая), в квантовой механике понятие частицы оказывается сложнее, чем в классической, и, в частности, понятия координаты и импульса утрачивают прежний смысл.
Точное задание координаты и импульса частицы оказывается лишенным смысла. Эти характеристики должны задаваться с некоторой неточностью. Это означает, что можно указать лишь ячейку в фазовом пространстве, в которой находится отображающая точка молекулы. В отличие от области, размеры которой неопределенны, ячейки, составляющие данную область, имеют определенный размер.
Следовательно, размер ячейки в отличие от размера области постоянен. Мы будем выбирать области одинакового размера и будем считать, что каждая содержит ячеек. [c.144]
Связи между материа тьными объектами многообразны бес конечны и неисчерпаемы науке неизбежны абстракции и приб лиженные модели Они полезны и целесообразны но должны использоваться в определенных границах Таковы понятия иде ального газа и идеального раствора равновесной и изолиро ванной систем обратимого процесса, широко используемые в физической химии, хотя Не всетда или лишь приближенно при годные для реальных систем [c.364]
Специалистов по катализу часто интересует доля поверхности для серии катализаторов сходного состава (например, С0/А12О3), которая имеет заметное сродство к данному субстрату. Поэтому для ряда задач катализа можно ввести различия в понятия геометрическая и физическая емкости монослоя.
Будем называть геометрической емкостью — емкость монослоя йт, измеренную по БЭТ стандартным инертным газом, например аргоном. Физической емкостью будем называть величину для данного катализатора в ряду химически сходных катализаторов, определенную для всех членов этого ряда одним и тем же способом.
Очевидно, что физическая емкость — величина условная, имеющая смысл лишь для сопоставления некоторых физико-химических характеристик реальных адсорбентов. [c.169]
Реальные газы
Реферат подготовила Магарамова Инесса
Модель идеального газа, используемая в молекулярно-кинетической теории газов, позволяющая описывать поведение разрежённых реальных газов при достаточно высоких температурах и низких давлениях. При выводе уравнения состояния идеального газа размерами молекул и их взаимодействием друг с другом пренебрегают. Повышение давления приводит к уменьшению среднего расстояния между молекулами, поэтому необходимо учитывать объём молекул и взаимодействие между ними. При высоких давлениях и низких температурах указанная модель идеального газа непригодна.
При рассмотрении реальных газов – газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях ≤10-9 м. и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
В ХХ в., по мере развития и представлений о строении атома и квантовой механики, было выяснено, что между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. Силы отталкивания считаются положительными, а силы взаимного притяжения – отрицательными.
2. Внутренняя энергия реального газа
Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул и из потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ.
Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, или, иными словами, против внутреннего давления, как известно из механики, идёт на увеличение потенциальной энергии системы.
Т.е. dA=p΄Vm=dП, или dП=a/V2m*dVm, откуда П=-а/Vm.
Знак минус означает, что молекулярные силы, создающие внутреннее давление р΄, являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа Um=CVT-a/Vm растёт с повышением температуры и увеличением объёма.
Если газ расширяется без теплообмена с окружающей средой и не совершает внешней работы, то на основании первого начала термодинамики получим, что U1=U2. Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется.
3. Уравнение Ван-дер-Ваальса
Учёт собственного объёма молекул и сил межмолекулярного взаимодействия привёл голландского физика И. Ван-дер-Ваальса (1837-1923) к выводу уравнения состояния реального газа. Ван-дер-Ваальсом в уравнение Клапейрона-Менделеева введены две поправки.
1. Учёт собственного объёма молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объём других молекул, сводится к тому, что фактический свободный объём, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm-b, где b- объём, занимаемый самими молекулами. Объём b равен утверждённому собственному объёму молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние меньше d, это означает, что для центров обеих молекул оказывается недоступным объём сферы радиусом d, объём, равный восьми объёмам молекулы, а в расчёте на одну молекулу – учетверённый объём молекулы.
Фазой называется термодинамически равновесное состояние вещества, отличающееся от других возможных равновесных состояний того же вещества. Если, например, в закрытом сосуде находится вода, то эта система является двухфазной: жидкая фаза – вода и газообразная фаза – смесь воздуха с водяными парами. Если в воду бросить кусочки льда, то эта система станет трёхфазной, в которой лёд является твёрдой фазой.
Часто понятие «фаза» употребляется в смысле агрегатного состояния, однако надо учитывать, что оно шире, чем «агрегатное состояние». В пределах одного агрегатного состояния вещество может находиться в нескольких фазах, отличающихся по своим веществам, составу и строению.
Переход вещества от одной фазы в другую – фазовый переход – всегда связан с качественными изменениями свойств вещества. Примером фазового перехода могут служить изменения агрегатного состояния вещества или переходы, связанные с изменениями в составе, строении и свойствах вещества (например, переход кристаллического вещества из одной модификации в другую).
Различают фазовые переходы двух родов. Фазовый переход первого рода (например, плавление, кристаллизация и т.д.) сопровождается поглощением или выделением вполне определённого количества теплоты, называемой теплотой фазового перехода.
Фазовые переходы первого рода характеризуются постоянством температуры, изменениями энтропии и объёма. Объяснение этому можно дать следующим образом. Например, при плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решётки. Подводимая при плавлении теплота идёт не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. При подобных переходах – из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние – степень беспорядка увеличивается и, с точки зрения второго начала термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет. В качестве примера на рисунке 1 показана температурная зависимость свободной энергии F, приходящейся на одну молекулу кристалла, при его превращении в пар. Верхняя ветвь отвечает кристаллическому состоянию, а нижняя ветвь представляет свободную энергию парообразной фазы. При низких температурах свободная энергия кристалла меньше, чем пара, и, следовательно, кристаллическое состояние выгоднее. При высоких температурах, наоборот, выгоднее существование парообразного состояния. Штриховыми линиями показаны области метастабильных, термодинамически неустойчивых состояний системы.










 Источник
Источник
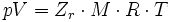







. Согласно этой трактовке, фазовые переходы второго рода связаны с изменением симметрии: выше точки перехода система, как правило, обладает более высокой симметрией, чем ниже точки перехода. Примерами фазовых переходов второго рода являются: переход ферромагнитных веществ (железа, никеля) при определённых давлении и температуре в парамагнитное состояние; переход металлов и некоторых сплавов при температуре, близкой к 0К, в сверхпроводящее состояние, характеризуемое скачкообразным уменьшением электрического сопротивления до нуля; превращение обыкновенного жидкого гелия при Т=2,9К в другую жидкую модификацию, обладающую свойствами сверхтекучести.</p><p>6. Третье начало термодинамики (Теорема Нернста)</p><p>При стремлении температуры любой равновесной термодинамической системы к абсолютному нулю ее энтропия стремится к некоторой универсальной постоянной величине, значение которой не зависит от каких-либо термодинамических параметров системы и может быть принято равной нулю:</p><p style=)

 состоянии, процесс охлаждения может происходить быстрее, чем переход их в равновесное (кристаллическое) состояние.</p><p>Другим следствием третьего начала термодинамики является невозможность использования уравнения Клапейрона-Менделеева для описания идеального газа при температурах, близких к абсолютному нулю. Так как для идеального газа на основании первого начала термодинамики можно записать:</p><p style=)
