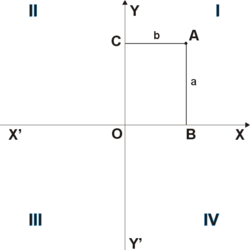
Что такое ордината точки
Обычно абсцисса относится к горизонтальной оси ( x ), а ордината относится к вертикальной оси ( y ) стандартного двухмерного графика.
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный; после: положительный).
СОДЕРЖАНИЕ
Этимология
В своей работе 1892 года « Vorlesungen über die Geschichte der Mathematik» (« Лекции по истории математики »), том 2, немецкий историк математики Мориц Кантор пишет:
Gleichwohl ist durch [Stefano degli Angeli] vermuthlich ein Wort in den Mathematischen Sprachschatz eingeführt worden, welches gerade in der analytischen Geometrie sich als zukunftsreich bewährt hat. […] Wir kennen keine ältere Benutzung des Wortes Abscisse in lateinischen Originalschriften. Vielleicht Kommt Дас Сусло в Uebersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte.
Использование слова «ордината» связано с латинским выражением «linea ordinata Applicata» или «параллельная линия».
В параметрических уравнениях
График линейной функции, его свойства и формулы
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Свойства линейной функции
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
Ось ординат
В прямоугольной системе координат ось Y’Y называется «осью ординат».
При построении графиков функций, ось ординат обычно используется как область значений функции.
См. также
Смотреть что такое «Ось ординат» в других словарях:
ось ординат — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN Y axisY line … Справочник технического переводчика
ось ординат — ordinačių ašis statusas T sritis automatika atitikmenys: angl. ordinate axis vok. Ordinatenachse, f rus. ординатная ось, f; ось ординат, f pranc. axe d ordonnées, m … Automatikos terminų žodynas
ось ординат — ordinačių ašis statusas T sritis fizika atitikmenys: angl. ordinate axis vok. Ordinatenachse, f rus. ось ординат, f pranc. axe d’ordonnées, m … Fizikos terminų žodynas
Ось (значения) — Ось (слово «ось» происходит от древнерусского «ость» долгий усик на плевеле каждого зерна колосовых растений или волос в пушном товаре) понятие некой центральной прямой, в том числе воображаемой прямой (линии): В технике:… … Википедия
ОСЬ — (1) в прикладной механике стержень, опирающийся на опоры и поддерживающий вращающиеся части машин (колёса вагонов) или механизмов (зубчатые колёса часов). В отличие от (см.) О. не передаёт полезного крутящего момента (см. (5)), а работает в… … Большая политехническая энциклопедия
Ось — У этого термина существуют и другие значения, см. Ось (значения). Ось (слово «ось» происходит от праславянской формы). В настоящее время означает серединную линию … Википедия
ординатная ось — ordinačių ašis statusas T sritis automatika atitikmenys: angl. ordinate axis vok. Ordinatenachse, f rus. ординатная ось, f; ось ординат, f pranc. axe d ordonnées, m … Automatikos terminų žodynas
Ordinate axis — Ось ординат … Краткий толковый словарь по полиграфии
Y-axis — Ось ординат, игреков … Краткий толковый словарь по полиграфии
определение — 2.7 определение: Процесс выполнения серии операций, регламентированных в документе на метод испытаний, в результате выполнения которых получают единичное значение. Источник … Словарь-справочник терминов нормативно-технической документации
ОРДИНАТА
— одна из декартовых координат точки.
Смотреть что такое «ОРДИНАТА» в других словарях:
Ордината — Когда данные изображаются в виде графика, ордината соответствует информации, содержащейся на вертикальной оси, или оси «У». При экспериментальных исследованиях на этой оси размещаются значения зависимой переменной. Психология. А Я. Словарь… … Большая психологическая энциклопедия
ОРДИНАТА — (от лат. ordinatus расположенный в порядке) одна из декартовых координат точки, обычно вторая, обозначаемая буквой y … Большой Энциклопедический словарь
ОРДИНАТА — ОРДИНАТА, ординаты, жен. (лат. ordinata расположенная на равных расстояниях) (мат.). В системе координат аналитической геометрии перпендикуляр на плоскости, опущенный из точки на ось абсцисс. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ордината — сущ., кол во синонимов: 1 • координата (4) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ордината — Разность долгот начала и конца профиля, измеренная на данной широте [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN ordinatedeparture … Справочник технического переводчика
ордината — В картографии координата, отсчитываемая по направлению, перпендикулярному осевому меридиану … Словарь по географии
ОРДИНАТА — одно из двух (трёх) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат … Большая политехническая энциклопедия
Ордината — Рис. 1 Ординатой (от лат. ordinatus расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямо … Википедия
ордината — (лат. ordinatus упорядоченный, расставленный в известном порядке) ееом. одно из двух (трех) чисел, определяющих положение точки на плоскости (в пространстве) относительно прямоугольной системы координат. Новый словарь иностранных слов. by EdwART … Словарь иностранных слов русского языка
ордината — ы; ж. [от лат. ordinatus упорядоченный, назначенный] Матем. Величина, определяющая положение некоторой точки на плоскости или в пространстве по оси Y в прямоугольной системе координат (ср. абсцисса, ордината). * * * ордината (от лат. ordinatus … … Энциклопедический словарь
ордината — ordinatė statusas T sritis fizika atitikmenys: angl. ordinate vok. Ordinate, f rus. ордината, f pranc. ordonnée, f … Fizikos terminų žodynas
Высшая математика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
Приведённый ознакомительный фрагмент книги Высшая математика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
1. Основные понятия. Системы координат. Прямые линии и их взаимное расположение
Координата точки — это величина, определяющая положение данной точки на плоскости, на прямой или кривой линии или в пространстве. Значение координаты зависит от выбора начальной точки, от выбора положительного направления и от выбора единицы масштаба.
Прямоугольная система координат состоит из двух взаимно перпендикулярных прямых — осей, точка их пересечения — начало координат О, ось ОХ — ось абсцисс, ось ОY — ось ординат. На осях выбираются масштаб и положительное направление.
Положение точки М определяется двумя координатами: абсциссой х и ординатой у. Записывается так: М(х, у). Оси координат образуют четыре координатных угла I, II, III, IV. Если точка находится в I координатном угле (квадранте), то и абсцисса, и ордината ее положительные, если — во II квадранте, то абсцисса отрицательна, а ордината положительна, если в — III квадранте, и абсцисса, и ордината отрицательны, если — в IV квадранте, положительна абсцисса, а ордината отрицательна. У точки, лежащей на оси ординат, абсцисса равна нулю, и наоборот, если точка лежит на оси абсцисс, то ее ордината равна нулю.
Косоугольной системой координат аналогична прямоугольной, только оси координат пересекаются под углом не равным прямому. Прямоугольная и косоугольная системы относятся к декартовой системе координат.
Полярная система координат состоит из полюса О и полярной оси ОХ, проведенной из полюса. Положение точки определяется полярным радиусом ρ (отрезок ОМ) и полярным углом φ. Для полярного угла берется его главное значение (от — π до π). Числа ρ, φ называются полярными координатами точки М.
Связь между координатами точки в прямоугольной и полярной системах координат: x = r cosφ, y = r sinφ или:
Общее уравнение прямой линии (система координат прямоугольная): Ах + Ву + С = 0 (А и В одновременно не равны нулю).
Если В не равно нулю, то уравнение прямой: у = ах + b (здесь а = — А / В, b = — С / В). Здесь а есть тангенс угла наклона прямой к положительному направлению оси абсцисс, b равно длине отрезка от начала координат до точки пересечения рассматриваемой прямой с осью ординат. Уравнение прямой, параллельной оси абсцисс: у = b, уравнение оси абсцисс: у = 0; уравнение прямой, параллельной оси ординат: х = с, уравнение оси ординат: х = 0.