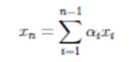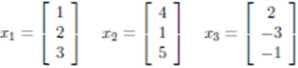Что такое ортогональная матрица

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Ортогональная матрица

Пример. Матрицы

Одно из подмножеств таких матриц имеют специальное название.

Произведение

Теорема. Произведение ортогональных матриц является ортогональной матрицей.

Определитель

Множество ортогональных матриц одинакового порядка образует группу относительно операции умножения.

Будет ли эта группа коммутативной, т.е. абелевой?

Норма

Теорема Кэли

Выражение через экспоненциал кососимметричной матрицы

Ортогональная матрица третьего порядка

Теорема [Эйлер]. Произвольное вращение твердого тела вокруг неподвижной точки, закрепленной в начале координат, задается ортогональной матрицей

Ортогональная матрица четвертого порядка: кватернионы

Характеристический полином, собственные числа

Произведение возратных полиномов будет возвратным полиномом. ♦

Пример. Найти характеристический полином и спектр матрицы

Применения

QR-разложение матрицы

Источники

[1]. Rodrigues O. Des lois géométriques qui régissent les déplacements d’un système solide dans l’espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire. Journal de Mathématiques Pures et Appliquées. 1840. V. 5, 380–440

[2]. Проскуряков И.В. Сборник задач по линейной алгебре. М.Наука. 1974; задача N 896.

Источник

Линейная алгебра для исследователей данных

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».

Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.

kdnuggets

В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.

Произведения векторов

Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy

называется следующее вещественное число:

Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество

Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть

Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:

След обладает следующими свойствами:

Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.

Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.

Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.

Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).

TimoElliott

Нормы

Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:

Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:

Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).

f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).

Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).

Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)

Другими примерами норм являются норма l₁

Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как

Нормы также могут быть определены для матриц, например норма Фробениуса:

Линейная независимость и ранг

линейно зависимы, так как x₃ = −2xₙ + x₂.

Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.

Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.

Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).

Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).

Ортогональные матрицы

Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м

атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.

Непосредственно из определений ортогональности и нормированности следует, что

Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n

для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.

TimoElliott

Область значений и нуль-пространство матрицы

Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,

Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть

Квадратичные формы и положительно полуопределенные матрицы

Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:

Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как

(или просто A > 0), а множество всех положительно определенных матриц часто обозначают

Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как

(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают

Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной

, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx

), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.

Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что

Собственные значения и собственные векторы

Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство

На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).

Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.

Источник

Ортогональная матрица

Это приводит к эквивалентной характеристике: матрица Q ортогональна, если ее транспонирование равно ее обратной :

Содержание

Обзор [ править ]

Примеры [ править ]

Ниже приведены несколько примеров небольших ортогональных матриц и возможные интерпретации.

Элементарные конструкции [ править ]

Нижние размеры [ править ]

Простейшими ортогональными матрицами являются матрицы 1 × 1 [1] и [−1], которые мы можем интерпретировать как тождество и отражение реальной линии через начало координат.

В 2 × 2 матрицы имеет вид

требования ортогональности удовлетворяют трем уравнениям

[ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] (rotation), [ cos ⁡ θ sin ⁡ θ sin ⁡ θ − cos ⁡ θ ] (reflection) <\displaystyle <\begin\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end><\text< (rotation), >>\qquad <\begin\cos \theta &\sin \theta \\\sin \theta &-\cos \theta \\\end><\text< (reflection)>>>

Тождество также является матрицей перестановок.

Высшие измерения [ править ]

Независимо от размера, всегда можно классифицировать ортогональные матрицы как чисто вращательные или нет, но для матриц 3 × 3 и более невращающиеся матрицы могут быть более сложными, чем отражения. Например,

[ − 1 0 0 0 − 1 0 0 0 − 1 ] and [ 0 − 1 0 1 0 0 0 0 − 1 ] <\displaystyle <\begin-1&0&0\\0&-1&0\\0&0&-1\end><\text< and >><\begin0&-1&0\\1&0&0\\0&0&-1\end>>

Однако у нас есть элементарные строительные блоки для перестановок, отражений и поворотов, которые применимы в целом.

Примитивы [ править ]

Хаусхолдера отражение строится из ненулевого вектора V как

Вращения Якоби имеют ту же форму, что и вращение Гивенса, но используются к нулю оба недиагональных элементов из более 2 × 2 симметричной подматрицы.

Свойства [ править ]

Свойства матрицы [ править ]

Обратное неверно; наличие определителя ± 1 не гарантирует ортогональности даже с ортогональными столбцами, как показано в следующем контрпримере.

Свойства группы [ править ]

( n − 1 ) + ( n − 2 ) + ⋯ + 1 = n ( n − 1 ) 2 <\displaystyle (n-1)+(n-2)+\cdots +1=<\frac <2>>>

Каноническая форма [ править ]

Алгебра Ли [ править ]

Оценка при t = 0 ( Q = I ) тогда подразумевает

Числовая линейная алгебра [ править ]

Преимущества [ править ]

Перестановки необходимы для успеха многих алгоритмов, включая «рабочую лошадку» исключения Гаусса с частичным поворотом (где перестановки выполняют поворот). Однако они редко появляются в явном виде как матрицы; их особая форма позволяет более эффективно представлять, например список из n индексов.

Разложения [ править ]

Ряд важных матричных разложений ( Голуб и Ван Лоан, 1996 ) включает ортогональные матрицы, в частности:

Примеры [ править ]

Например, рассмотрим неортогональную матрицу, для которой простой алгоритм усреднения занимает семь шагов

[ 3 1 7 5 ] → [ 1.8125 0.0625 3.4375 2.6875 ] → ⋯ → [ 0.8 − 0.6 0.6 0.8 ] <\displaystyle <\begin3&1\\7&5\end>\rightarrow <\begin1.8125&0.0625\\3.4375&2.6875\end>\rightarrow \cdots \rightarrow <\begin0.8&-0.6\\0.6&0.8\end>>

и какое ускорение сокращается до двух ступеней (с γ = 0,353553, 0,565685).

[ 3 1 7 5 ] → [ 1.41421 − 1.06066 1.06066 1.41421 ] → [ 0.8 − 0.6 0.6 0.8 ] <\displaystyle <\begin3&1\\7&5\end>\rightarrow <\begin1.41421&-1.06066\\1.06066&1.41421\end>\rightarrow <\begin0.8&-0.6\\0.6&0.8\end>>

Грам-Шмидт дает худшее решение, показанное расстоянием Фробениуса 8,28659 вместо минимального 8,12404.

[ 3 1 7 5 ] → [ 0.393919 − 0.919145 0.919145 0.393919 ] <\displaystyle <\begin3&1\\7&5\end>\rightarrow <\begin0.393919&-0.919145\\0.919145&0.393919\end>>

Рандомизация [ править ]

Ближайшая ортогональная матрица [ править ]

Это можно комбинировать с вавилонским методом извлечения квадратного корня из матрицы, чтобы получить повторение, которое квадратично сходится к ортогональной матрице:

Q n + 1 = 2 M ( Q n − 1 M + M T Q n ) − 1 <\displaystyle Q_=2M\left(Q_^<-1>M+M^ <\mathrm>Q_\right)^<-1>>

Использование аппроксимации первого порядка обратной и той же инициализации приводит к измененной итерации:

Крутить и закреплять [ править ]

Прямоугольные матрицы [ править ]

Для этих матриц нет стандартной терминологии. Иногда их называют «ортонормированными матрицами», иногда «ортогональными матрицами», а иногда просто «матрицами с ортонормированными строками / столбцами».

Источник

Ортогональная матрица

Содержание

Свойства

Другими словами, скалярное произведение строки на саму себя равно 1, а на любую другую строку — 0. Так же и для столбцов.

Примеры

См. также

Примечания

Полезное

Смотреть что такое «Ортогональная матрица» в других словарях:

ортогональная матрица — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN orthogonal matrix … Справочник технического переводчика

ортогональная матрица — ortogonalioji matrica statusas T sritis fizika atitikmenys: angl. orthogonal matrix vok. orthogonale Matrix, f rus. ортогональная матрица, f pranc. matrice orthogonale, f … Fizikos terminų žodynas

ОРТОГОНАЛЬНАЯ МАТРИЦА — матрица над коммутативным кольцом R с единицей 1, для к рой транспонированная матрица совпадает с обратной. Определитель О. м. равен +1. Совокупность всех О. м. порядка пнад Rобразует подгруппу полной линейной группы GLn (R). Для любой… … Математическая энциклопедия

Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия

Матрица (в математике) — Матрица в математике, система элементов aij (чисел, функций или иных величин, над которыми можно производить алгебраические операции), расположенных в виде прямоугольной схемы. Если схема имеет m строк и n столбцов, то говорят о (m n) матрице.… … Большая советская энциклопедия

Ортогональная группа — Группа (математика) Теория групп … Википедия

Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия

Матрица — I Матрица (нем. Matrize, от латинского matrix матка, источник, начало) в полиграфии, 1) сменный элемент литейной формы с углублённым (иногда фотографическим) изображением буквы или знака, используемый при отливке типографских… … Большая советская энциклопедия

ОРТОГОНАЛЬНАЯ ГРУППА — группа всех линейных преобразований n мерного векторного пространства Vнад полем k, сохраняющих фиксированную невырожденную квадратичную форму Q на V(т. е. таких линейных преобразований j, что Q(jn(v))=Q(v) для любого ). О. г. принадлежит к числу … Математическая энциклопедия

Источник

Это приводит к эквивалентной характеристике: матрица Q ортогональна, если ее транспонирование равно ее обратной :

СОДЕРЖАНИЕ

Обзор

ты ⋅ v знак равно ( Q ты ) ⋅ ( Q v ) <\ Displaystyle <\ mathbf > \ cdot <\ mathbf > = \ left (Q <\ mathbf > \ right) \ cdot \ left (Q <\ mathbf > \ right) >

Примеры

Ниже приведены несколько примеров небольших ортогональных матриц и возможные интерпретации.

Элементарные конструкции

Меньшие размеры

Простейшими ортогональными матрицами являются матрицы 1 × 1 [1] и [−1], которые мы можем интерпретировать как идентичность и отражение реальной линии через начало координат.

В 2 × 2 матрицы имеет вид

требования ортогональности удовлетворяют трем уравнениям

Тождество также является матрицей перестановок.

Высшие измерения

Независимо от размерности, всегда можно классифицировать ортогональные матрицы как чисто вращательные или нет, но для матриц 3 × 3 и больше невращающиеся матрицы могут быть более сложными, чем отражения. Например,

Однако у нас есть элементарные строительные блоки для перестановок, отражений и поворотов, которые применимы в целом.

Примитивы

Хаусхолдера отражение строится из ненулевого вектора V как

Вращения Якоби имеют ту же форму, что и вращение Гивенса, но используются к нулю оба недиагональных элементов из более 2 × 2 симметричной подматрицы.

Характеристики

Свойства матрицы

Обратное неверно; наличие определителя ± 1 не гарантирует ортогональности даже с ортогональными столбцами, как показано в следующем контрпримере.

Свойства группы

Каноническая форма

Алгебра Ли

Q Т Q знак равно я <\ Displaystyle Q ^ <\ mathrm> Q = I>

Q ˙ Т Q + Q Т Q ˙ знак равно 0 <\ displaystyle <\ dot > ^ <\ mathrm> Q + Q ^ <\ mathrm> <\ dot > = 0>

Оценка при t = 0 ( Q = I ) тогда подразумевает

Числовая линейная алгебра

Преимущества

Перестановки необходимы для успеха многих алгоритмов, включая «рабочую лошадку» исключения Гаусса с частичным поворотом (где перестановки выполняют поворот). Однако они редко появляются в явном виде в виде матриц; их особая форма позволяет более эффективно представлять, например список из n индексов.

Разложения

Ряд важных матричных разложений ( Голуб и Ван Лоан, 1996 ) включает ортогональные матрицы, в частности:

Примеры

Например, рассмотрим неортогональную матрицу, для которой простой алгоритм усреднения занимает семь шагов

и какое ускорение сокращается до двух ступеней (с γ = 0,353553, 0,565685).

Грам-Шмидт дает худшее решение, показанное расстоянием Фробениуса 8,28659 вместо минимального 8,12404.

Рандомизация

Ближайшая ортогональная матрица

Это можно комбинировать с вавилонским методом извлечения квадратного корня из матрицы, чтобы получить повторение, которое квадратично сходится к ортогональной матрице:

Использование аппроксимации первого порядка обратной и той же инициализации приводит к измененной итерации:

Спин и булавка

Прямоугольные матрицы

Для этих матриц нет стандартной терминологии. Их по-разному называют «полуортогональными матрицами», «ортонормированными матрицами», «ортогональными матрицами», а иногда просто «матрицами с ортонормированными строками / столбцами».

Источник

• ← Что такое ортогнатический прикус
• Что такое ортогональные преобразования →