Что такое ось симметрии 4 класс у квадрата

Осевая и центральная симметрия

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

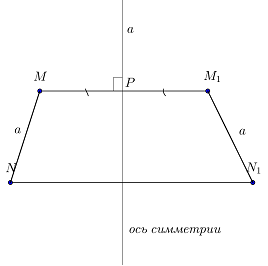
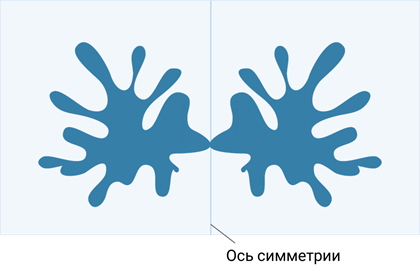
Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

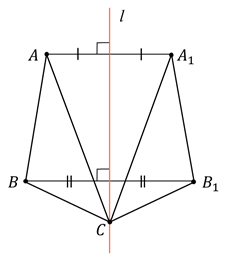
Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

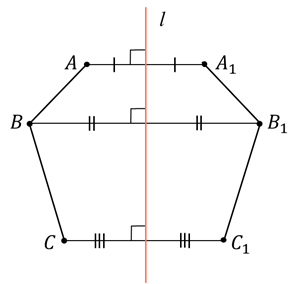
Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник

Что называется осевой симметрией

Что такое осевая симметрия в геометрии

Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.

Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – S_n, таким образом симметрия точек A и B обозначается так:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.

Свойства осевой симметрии

Теорема и доказательство

Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.

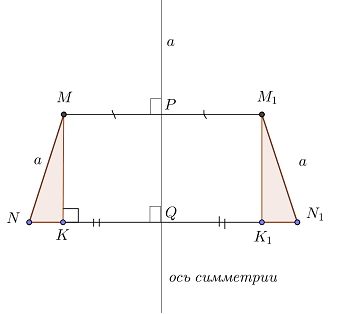
Если отрезок MN симметричен отрезку M₁N₁ относительно прямой a, то MN = M₁N₁.

Чтобы доказать, что MN = M₁N₁, сделаем дополнительные построения:

Докажем, что прямоугольные треугольники MNK и M₁N₁K₁ равны. Стороны MN и M₁N₁ являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.

Точка N отобразилась в точку N₁, значит:

Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M₁N₁, что и требовалось доказать.

Фигуры, обладающие симметрией

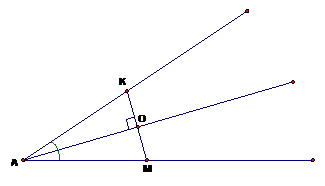
Осевой симметрией обладает угол, а биссектриса является осью симметрии.

Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:

Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.

Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.

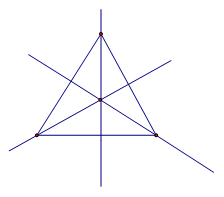
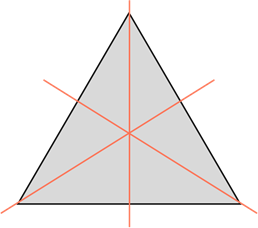
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

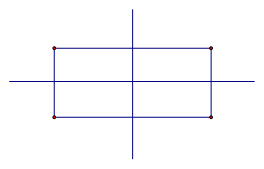
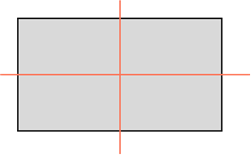
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

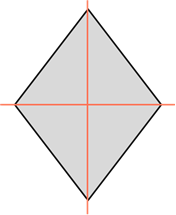
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

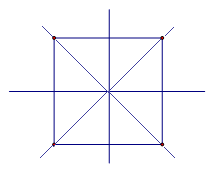
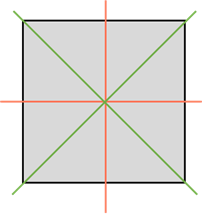
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

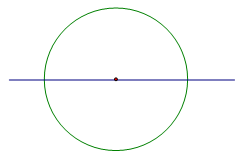
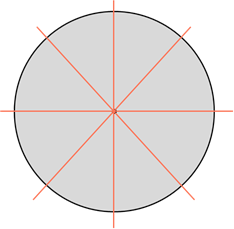
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни

Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.

Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.

Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.

Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.

Источник

Методическая разработка внеурочного занятия «Осевая симметрия» (4 класс)

Выбранный для просмотра документ Конспект. Осевая симметрия. 4 класс.docx

Муниципальное бюджетное общеобразовательное учреждение города Ульяновска «Средняя школа № 42»

Семенова Анна Николаевна

учитель начальных классов

Методическая разработка занятия внеурочной деятельности курса

«Математика и конструирование»

Тема: «Осевая симметрия»

Тема: «Осевая симметрия»

Цель занятия : дать представление об осевой симметрии; научить находить осевую симметрию в фигурах.

развивать умение видеть симметричные фигуры, различать фигуры, имеющие одну или несколько осей симметрии;

формировать умение проводить практическими и графическими способами оси симметрии в фигурах;

воспитывать интерес к математике, чувство взаимовыручки, любознательность, аккуратность.

— регулятивные : принимать и сохранять цели и задачи учебной деятельности, искать и находить средства их достижения; планировать, контролировать и оценивать действия в соответствии с поставленной задачей;

— познавательные : выделять существенные характеристики объекта; осуществлять поиск и выделять необходимую информацию для выполнения заданий;

— коммуникативные : строить речевое высказывание в устной форме; принимать участие в определении общей цели и путей ее достижения; признавать возможность существования различных точек зрения;

— личностные: осуществлять самоконтроль и самооценку результатов деятельности; применять умения и навыки самостоятельной деятельности, осознавать личную ответственность за ее результат.

Методическое оснащение: ПК, интерактивная доска, презентация, у каждого ученика: одна из геометрических фигур (квадрат, прямоугольник, равносторонний и прямоугольный треугольники, круг), линейка, ножницы, цветная бумага; карточки с заданиями.

Самоопределение к деятельности

Работа по теме занятия

Подведение итогов занятия

Учащиеся поделены на группы

Учитель. Давайте улыбнемся друг другу.

Начинайте день с улыбки

С добрым сердцем и тогда

Будет радость и удача

Вам сопутствовать всегда!

Пусть улыбки и хорошее настроение будут верными спутниками на сегодняшнем занятии и помогут разобраться во всем и справиться с любой задачей.

Самоопределение к деятельности

Учитель. Посмотрим отрывок из мультфильма «Крошка Енот» и вспомним, какому герою помогла улыбка (Слайд 2) (Крошке Еноту)

Учитель. Рассмотрите иллюстрацию к мультфильму. (Слайд 3)

Учитель. Что увидел Енотик в пруду? (Свое отражение)

Учитель. Что вы можете сказать об изображении Енота и его отображении в воде? (Отображение получилось перевернутое.)

Учитель. Изменились ли правая и левая сторона? (Нет).

Учитель. Ребята, а где еще отражаются предметы? (В зеркале).

Учитель. Чтобы узнать, как называется зеркальное отображение в математике, нам нужно разгадать ребус. (Слайд 4) (Симметрия.)

Учитель. Сегодня на занятии мы прикоснемся к удивительному математическому понятию «симметрия». Узнаем, что такое симметрия, ось симметрии. Научимся строить симметричные фигуры. Узнаем, где встречается симметрия.

Работа по теме занятия

Учитель. Слово «симметрия» в переводе с греческого звучит как «гармония», означая красоту, соразмерность, пропорциональность, одинаковость в расположении частей.

Учитель. Возьмите лист, на котором изображен треугольник (№1). Обведите треугольник 2-3 раза, сильно нажимая на карандаш.

Перегните лист пополам так, чтобы треугольник оказался внутри.

Не разгибая лист, снова обведите треугольник, сильно нажимая на карандаш.

Раскройте лист. Что у вас получилось? (Два треугольника)

Учитель. По линии сгиба проведите по линейке прямую.

Учитель. Линия сгиба будет осью симметрии этих двух треугольников.

Учитель. Если снова согнуть лист по оси симметрии (линии сгиба), что произойдет с треугольниками? (Они совпадут.)

Учитель. Как мы называем фигуры, которые совпадают? (Равными.)

Учитель. Что интересного заметили в расположении треугольников относительно линии сгиба. (Они расположены на одинаковом расстоянии относительно линии сгиба.)

Учитель. Возьмите лист бумаги (№2). Что с ним нужно сделать с листочком, чтобы получить симметричную фигуру? (Сложить пополам)

Учитель. Перегните его пополам и хорошо разгладьте линию сгиба.

Учитель. Приложите шаблон к линии сгиба, обведите его (елочку).

Вырежьте силуэт, не перерезая линию сгиба. Расправьте лист. Что у вас получилось? (Елочка)

Учитель. Что вы можете сказать о правой и левой частях елочки (Они одинаковые.)

Учитель. Вы разделены на группы. Вспомните правила работы в группе. ( 1. В группе должен быть ответственный ; 2. Работать должен каждый на общий результат ; 3. Один говорит, другие слушают; 4. Своё несогласие высказывай вежливо; 5. Если не понял, переспроси) (Слайд 6)

Учитель. Выберите руководителя группы, который будет следить за выполнением задания.

Учитель. В конвертах №3 у вас лежат геометрические фигуры. У одной группы квадраты, у другой прямоугольники, у третьей по два треугольника, у четвертой круги. Руководители группы раздайте фигуры.

Учитель. Что нужно сделать, чтобы провести ось симметрии? (Перегнуть фигуры пополам.)

Учитель. Возьмите фигуры и проведите, если это возможно, оси симметрии в данных фигурах. После выполнения задания ответьте на вопросы: «Симметрична фигура или нет? Сколько осей симметрии можно провести?»

Учитель. Рассмотрим квадрат. Симметричен ли он? (Да). (Слайд 7)

Учитель. Докажите! (Если перегнуть квадрат пополам, то две половинки совпадут.)

Учитель. Сколько осей симметрии у квадрата? (Четыре).

Учитель. Рассмотрим прямоугольник. Симметричен ли он? (Да). (Слайд 8)

Учитель. Докажите! (Если перегнуть прямоугольник пополам, то две половинки совпадут.)

Учитель. Сколько осей симметрии у прямоугольника? (Две).

Учитель. Рассмотрим треугольники. Какие это треугольники, если измерить длины сторон этих треугольников? (Равносторонний и разносторонний.)

Учитель. Рассмотрим равносторонний треугольник Симметричен ли он? (Да).

Учитель. Сколько осей симметрии у этого треугольника? (Три). (Слайд 9)

Учитель. А теперь проверим разносторонний треугольник. Симметричен ли он? (Нет).

Учитель. Почему? (При перегибании половинки не совпадают).

Учитель. Рассмотрим круг. Является ли круг симметричной фигурой. (Да)

Учитель. А сколько у него осей симметрии? (Много). (Слайд 10)

Учитель. Еще в Древней Греции круг считался венцом совершенства. И не случайно. У него больше всего осей симметрии.

Физкультминутка (Слайд 11)

«Мы пойдем налево, мы пойдем направо»

Учитель. Мы выяснили, что в математике встречается симметрия. Но только ли в этой науке она может быть?

Учитель. Чтобы ответить на этот вопрос проведем исследование. Каждая группа получает свой маршрутный лист. (Конверт №4 )

Учитель. Выполнив задание, прикрепите его на доску с помощью магнита и приготовьтесь к защите. Алгоритм выступления у вас на парте. Во время выполнения задания вы можете пользоваться справочниками, энциклопедиями и словарями.

Темы вслух не оглашаются.

Учитель. Руководителя группы, которая работала над этой темой (учитель показывает название темы), прошу приступить к защите. Итак, тема вашего задания …

(1 группа. Тема нашего задания «Симметрия в мире животных». Каждое животное (насекомое, рыба, птица, зверь, …) состоит из двух половин – левой и правой. Поэтому у них симметричны правое и левое ухо, правый и левый глаз, правая и левая лапа, правый и левый рог, …). Значит можно сделать вывод, что симметрия встречается в животном мире.

2 группа. Тема нашего задания «Симметрия в мире растений». Симметрия хорошо видна на примере деревьев, их листьев, симметрию можно увидеть среди цветов. Значит можно сделать вывод, что симметрия встречается в растительном мире.

3 группа. Тема нашего задания «Симметрия в архитектуре». У многих архитектурных сооружений правая сторона похожа на левую. В них можно провести ось симметрии. Значит можно сделать вывод, что симметрия встречается в архитектуре.

4 группа. Тема нашего задания «Симметрия в русском языке». В русском языке встречаются буквы, имеющие одну или две оси симметрии, есть буквы, которые не имеют оси симметрии. Также в русском языке встречаются слова и целые предложения, которые имеют ось симметрии. Такие слова и предложения называются палиндромами. Значит, можно сделать вывод, что симметрия встречается в русском языке.)

На доске возле стрелочек прикреплены выполненные задания, некоторые стрелочки остаются пустыми :

Учитель. Как вы думаете, почему остались пустые стрелочки ? (Симметрия может встречаться не только в указанных группах.)

Учитель. Где же может еще встречаться симметрия ? (в технике, в спорте, в танце, в искусстве, …) (Слайд 12-15)

Рефлексия (Слайд 16)

Учитель. Продолжите предложения:

Подведение итогов занятия

Учитель. Как называется тема, над которой мы работали? (Симметрия)

Учитель. Какие фигуры можно назвать симметричными? (Фигуры, имеющие ось симметрии и совпадающие при перегибании).

Учитель. Что такое ось симметрии? (Прямая линия, по которой можно сложить фигуру, её половинки совпадут.)

Тадж-Маха́л — мавзолей мечеть в Инди и

Самый высокий в мире отель— Бурдж аль Араб или отель Парус в Дубаи (Объединенные Арабские Эмираты)

Источник

Симметрия

Урок 29. Наглядная геометрия 5–6 классы ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Симметрия»

Опыты с зеркалами, которые мы проводили на прошлом занятии, позволили нам прикоснуться к удивительному миру симметрии.

В переводе с греческого слово «симметрия» означает «соразмерность, пропорциональность, одинаковость в расположении частей».

Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то, что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким образом…

А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура).

Поэтому такая симметрия называется зеркальной (или осевой, если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии.

Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.

С симметрией мы постоянно встречаемся в повседневной жизни. Люди используют симметрию в орнаментах, предметах быта, технике. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придаёт гармоничность, законченность. Симметрия также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.

Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил. Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии кляксы.

Получается, что клякса имеет одну (вертикальную) ось симметрии.

А вот у снежинки 6 линий сгиба и все они являются осями симметрии.

У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.

Так, прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон. То есть, вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии, половинки фигуры совпадут.

Ромб также обладает двумя осями симметрии. Это прямые, которые содержат его диагонали.

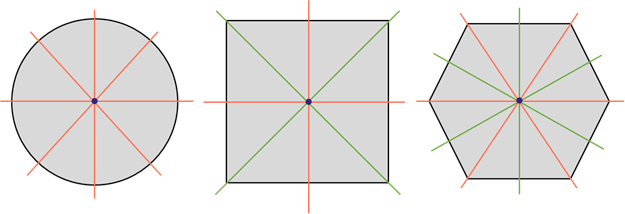
Квадрат имеет четыре оси симметрии. Две проходят через середины его противоположных сторон. И ещё две – это прямые, которые содержат его диагонали.

Круг. Его осью симметрии является любая прямая, которая проходит через его центр, то есть содержит диаметр круга. А значит, круг имеет бесконечно много осей симметрии

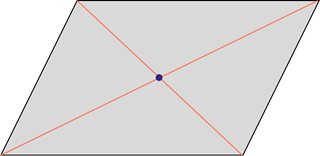
Теперь посмотрите на следующую фигуру. Это произвольный параллелограмм. У него нет ни одной оси симметрии.

У произвольного треугольника тоже нет осей симметрии.

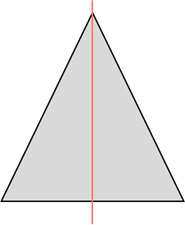
У равнобедренного треугольника есть одна ось симметрии.

У равностороннего (то есть у правильного) треугольника – три оси симметрии.

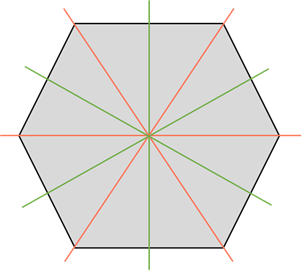
Теперь посмотрите на шестиугольник. У него три оси симметрии, которые проходят через противоположные вершины, и ещё три оси, которые проходят через середины противоположных сторон. То есть всего шесть осей симметрии.

Таким образом, мы можем сказать, что круг – «самая симметричная» фигура из рассмотренных, так как он имеет бесконечно много осей симметрии.

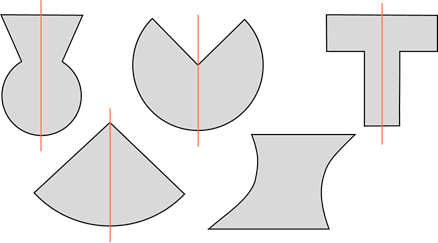
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из них лишняя.

Итак, первая фигура напоминает замочную скважину. Она имеет одну ось симметрии.

Вторая фигура тоже имеет одну ось симметрии.

У третьей фигуры (в виде буквы Т) одна ось симметрии.

У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси симметрии. И поэтому она лишняя.

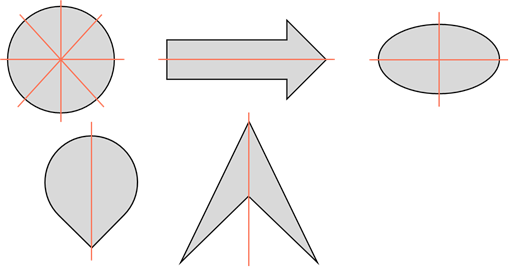
Теперь давайте посмотрим на следующие пять фигур. Что у них общего?

Первая фигура – круг. Выше мы выяснили, что у круга бесконечно много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая фигура имеет хотя бы одну ось симметрии.

На предыдущем занятии мы с вами проводили опыт с двумя плоскими зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали симметричные фигуры.

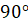
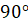
Давайте изобразим в виде прямых два зеркала под углом друг к другу. Затем нарисуем в одном из углов некоторую линию и, не пользуясь настоящими зеркалами, дорисуем её до симметричной фигуры, которая получилась бы при отражении в зеркалах. Полученная фигура имеет две оси симметрии. Понятно, что угол ними равен .

Посмотрите на рассмотренные выше фигуры, которые имеют две оси симметрии. Угол между осями равен .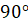

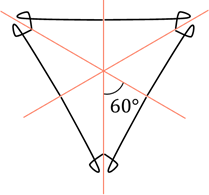
Если, например, мы поставим зеркала под углом 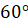друг к другу, то линия отразится 5 раз, а полученная фигура будет иметь 3 оси симметрии.

Давайте научимся точно строить отражение фигуры в зеркале. Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную 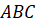и построим её отражение в зеркале.

Итак, из вершин , и опускаем перпендикуляры на прямую l. Затем продолжаем их «за зеркало» на такое же расстояние (равное длине соответствующего отрезка). Получаем точки , и . Соединяем эти точки. Ломаная является отражение ломаной .

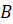
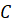
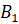
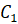
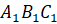
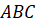
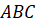
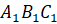
Можно сказать, что ломаная симметрична ломаной относительно прямой l.

Построим с вами треугольник, симметричный треугольнику 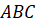относительно прямой l.

Из вершин и опустим перпендикуляры на прямую l. Затем продолжим их за прямую l на такое же расстояние (равное длине соответствующего отрезка). Получим точки и .

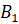
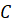
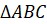
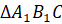
При этом точка осталась на месте. Она лежит на оси симметрии. Она симметрична сама себе. и симметричны относительно прямой l.

А сейчас посмотрите на рисунок.

Давайте выясним, симметрична ли точка точке относительно прямой l. Для этого мы соединим точки и . Затем с помощью угольника проверим, перпендикулярна ли прямая l отрезку . Перпендикулярна.

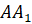
Потом с помощью линейки проверим, делит ли прямая l отрезок и пополам. Делит.

Значит, точки и симметричны относительно прямой l.

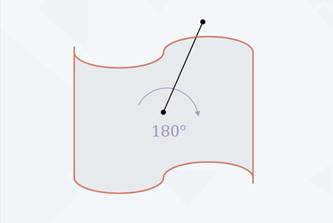
Кроме симметрии относительно прямой существует ещё симметрия относительно точки, так называемая центральная симметрия. Она характеризуется наличием центра симметрии – точки О, которая обладает определённым свойством. Можно сказать, что точка О является центром симметрии, если при повороте вокруг точки О на 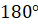фигура переходит сама в себя.

Понятие центральной симметрии распространяется и на трёхмерное пространство.

Проверить, является ли фигура центрально-симметричной или нет, можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем, проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру на 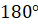вокруг иголки. Если фигура «вошла» в свой контур, то она центрально-симметричная.

Сейчас посмотрите на плоские фигуры, которые имеют и центр симметрии, и оси симметрии.

Это круг. Выше мы сказали, что он имеет бесконечно много осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии круга является его центр.

Квадрат имеет четыре оси симметрии. Центром симметрии квадрата является точка пересечения его диагоналей.

У шестиугольника шесть осей симметрии. Центром его симметрии является точка пересечения его диагоналей.

Выше мы сказали, что произвольный параллелограмм не имеет ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его диагоналей.

А вот, например, равнобедренный треугольник имеет ось симметрии, но не имеет центра симметрии. То же самое можно сказать и про пятиугольник, у которого есть оси симметрии, но центра симметрии нет.

Источник