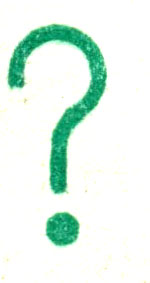Что такое осевая линия

Типы линий на чертеже и их назначение по ГОСТу

Ни один чертеж не имеет смысла, если в нем отсутствуют специальные линии. Они являются основным элементом, с помощью которого специалисты успешно читают и понимают чертеж.

Какие бывают линии, зачем они нужны и что по этому поводу говорит ГОСТ — в этой статье.

Что представляют собой линии и ГОСТ

Чтение чертежа существенно облегчается и становится проще, когда используют различные варианты линий — у них различные вид и назначение. Все эти варианты установлены и регламентируются ГОСТами.

Один из них — ГОСТ 2.303-68 о Единой системе конструкторской документации.

ГОСТ считается основным: его используют преподавательский состав и инженеры, работа которых непосредственно связана с созданием чертежей. Он же лег в основу более усовершенствованного стандарта 2.109-73.

На первом этапе черчения нужно использовать сплошные тонкие линии. Только после уточнения формы, габаритов, размещения картинки, удаления дополнительных линий, берут вспомогательные линии, предписанные стандартом.

Какие типы линий применяются в чертежах

Выделяют 7 основных типов линий для создания чертежей:

Параметр толщины толстой сплошной линии — ориентир для других. Но есть один нюанс: каждый тип линий по всему чертежу прочерчивается с одинаковой толщиной.

Важно, чтобы осевые и центровые линии выходили за пределы контура картинки на 2-5 мм и в конце была не точка, а штрих.

Наименование

Начертание

Сплошная толстая линия

Сплошная тонкая с изломами

Штрихпунктирная с двумя точками тонкая

Наименование

Толщина линии по отношению к толщине основной линии

Основное назначение

Сплошная толстая линия

Сплошная тонкая с изломами

Длинные линии обрыва

Штрихпунктирная с двумя точками тонкая

Последовательность черчения линий

Разработана специальная инструкция, определяющая последовательность отображения линий.

Первый этап — подготовка листа, в которую входит оформление рамки и разметка мест будущих участков детали.

Второй этап — прочерчивание центровых и осевых линий. Начинают процесс черчения с горизонтальных отрезков.

Третий этап — отображение окружностей и дуг радиусов. Вначале — меньшие.

Четвертый этап — последовательное проведение линий: горизонтальных, вертикальный, наклонных.

Пятый этап — обозначение участков детали с помощью специальных линий.

После этого готовый эскиз можно прорисовывать чернилами.

Как прорисовываются линии на чертеже

Выверенный алгоритм прорисовки делает изображение четче и позволяет добиться правильных пропорций толщины линий.

Источник

ЛИНИЯ ОСЕВАЯ

ЛИНИЯ ОСЕВАЯ штрих-пунктирная линия, изображающая на чертеже ось предмета или его поверхности

(Болгарский язык; Български) — осова линия

(Чешский язык; Čeština) — osová čára; osa

(Немецкий язык; Deutsch) — Achslinie; Mittellinie

(Венгерский язык; Magyar) — tengelyvonal

(Монгольский язык) — тэнхлэгийн шугам

(Польский язык; Polska) — linia osi

(Румынский язык; Român) — linie axială

(Сербско-хорватский язык; Српски језик; Hrvatski jezik) — osna linija

(Испанский язык; Español) — línea axial

(Английский язык; English) — center line

(Французский язык; Français) — ligne axiale

Смотреть что такое «ЛИНИЯ ОСЕВАЯ» в других словарях:

линия осевая — Штрих пунктирная линия, изображающая на чертеже ось предмета или его поверхности [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики проектирование, документация EN center line DE Achslinie FR Mittellinie … Справочник технического переводчика

Линия осевая — пунктирная линия, изображающая на чертеже ось предмета или его поверхности. [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Рубрика термина: Проектирование Рубрики энциклопедии: Абразивное оборудование, Абразивы,… … Энциклопедия терминов, определений и пояснений строительных материалов

осевая линия — средняя линия — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы средняя линия EN centerline … Справочник технического переводчика

осевая линия рядка сахарной свеклы — Условная линия, проходящая посередине рядка сахарной свеклы. [ГОСТ 20578 85] Тематики свекла сахарная Обобщающие термины уход за посевами сахарной свеклы EN axis line of a beet row DE Mittellinie des Zuckerrübenreihe FR ligne axiale de ligne de… … Справочник технического переводчика

ЛИНИЯ — (1) общая часть двух смежных областей поверхности; (2) Л. автоматическая комплекс станков и машин, основного и вспомогательного оборудования, автоматически выполняющих в технологической последовательности и с заданным ритмом весь процесс… … Большая политехническая энциклопедия

осевая линия лопасти — (15) [ГОСТ 25815 83 (СТ СЭВ 3042 81)] Тематики винты гребные Обобщающие термины элементы и размеры гребных винтов … Справочник технического переводчика

осевая линия профиля — (53) [ГОСТ 25815 83 (СТ СЭВ 3042 81)] Тематики винты гребные Обобщающие термины элементы и размеры гребных винтов … Справочник технического переводчика

осевая линия трубопровода — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN developed length … Справочник технического переводчика

осевая линия — 3.1.8 осевая линия (pitch line) Р: Условная линия, соединяющая передние кромки ступеней от верхней площадки до нижней площадки марша (см. рисунок 1). Источник: ГОСТ Р ИСО 14122 3 2009: Безопасность машин. Средства доступа к машинам стационарные.… … Словарь-справочник терминов нормативно-технической документации

осевая линия зоны обнаружения извещателя охранного комбинированного радиоволнового с инфракрасным пассивным (осевая линия) — 3.12 осевая линия зоны обнаружения извещателя охранного комбинированного радиоволнового с инфракрасным пассивным (осевая линия): Условная линия, исходящая от извещателя и являющаяся осью симметрии зоны обнаружения. Источник … Словарь-справочник терминов нормативно-технической документации

Источник

Что такое осевая линия

§ 2. Линии чертежа

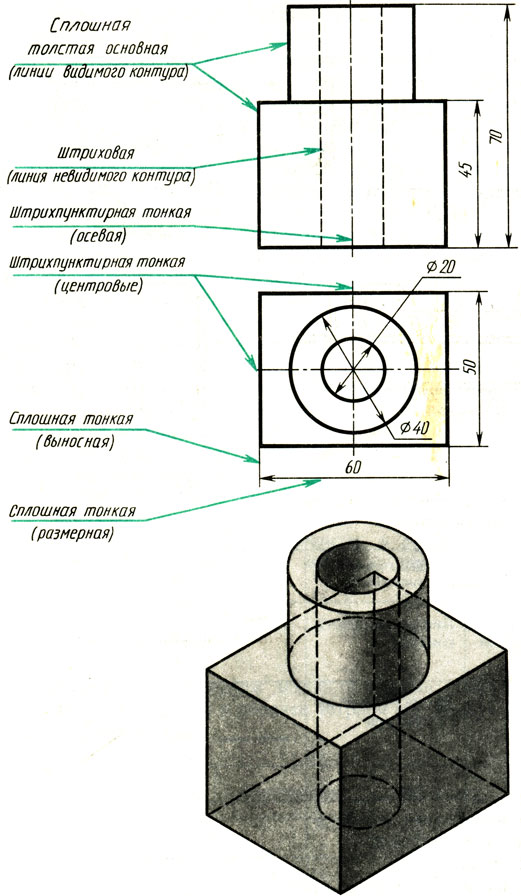
Рассмотрите рис. 9. Какими линиями обведены на нем изображения?

Чтобы чертежи было легче читать, ГОСТ 2.303-68 (СТ СЭВ 1178-78) устанавливает линии для чертежей всех отраслей промышленности и строительства.

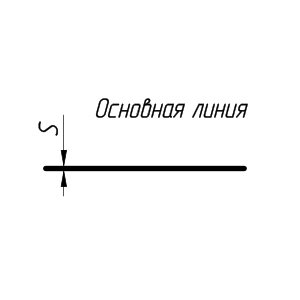
Сплошная толстая основная линия. Для изображения видимых контуров предметов применяется линия, называемая сплошной толстой основной. Толщина этой линии, обозначаемая латинской буквой s, установлена стандартом в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения. Выбранная толщина s линии должна быть одинаковой для всех изображений на данном чертеже.

Такой линией обведено изображение видимых очертаний предмета на рис. 9.

Рис. 9. Линии чертежа

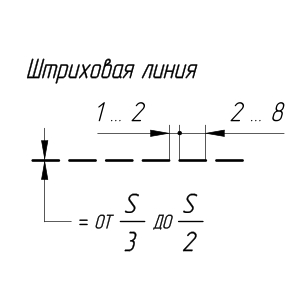
Штриховая линия. Для невидимых очертаний предмета применяют линию, которую называют штриховой. На рис. 9 такой линией показано невидимое на данном изображении отверстие, находящееся внутри детали.

Штриховая линия состоит из штрихов (черточек) одинаковой длины. Их длина установлена стандартом в пределах от 2 до 8 мм (для ученических чертежей рекомендуется 4 мм). Длина всех штрихов в линии должна быть приблизительно одинаковой. Расстояние между штрихами должно составлять от 1 до 2 мм и быть приблизительно одинаковым в линии. Толщина штрихов зависит от выбранной толщины сплошной толстой основной линии и должна составлять от s/2 до s/3. Это означает, что толщина штриховой линии в 2-3 раза тоньше основной.

Штриховые линии должны начинаться и заканчиваться штрихами (рис. 10).

Неверно называть штриховую линию пунктирной. Раньше ее чертили в виде точек. По-немецки пункт означает точка, отсюда и название пунктирная. Теперь это название не соответствует характеру линии.

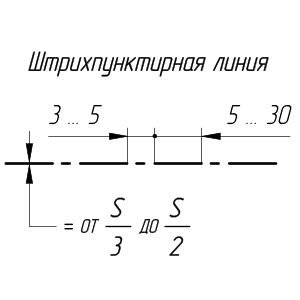
Штрихпунктирная тонкая линия. Для проведения осевых, а также центровых линий, указывающих центры окружностей и дуг, используют линию, называемую штрихпунктирной тонкой, которая состоит из длинных тонких штрихов и точек между ними. Длина штрихов от 5 до 30 мм, расстояние между ними от 3 до 5 мм (для учебных чертежей длину штрихов рекомендуют 20 мм). Толщину штрихпунктирной линии берут от s/2 до s/3.

Осевые и центровые линии концами должны выступать за контур изображения на 2-5 мм (см. рис. 10) и оканчиваться штрихом, а не точкой. Положение центра окружности определяется пересечением штрихов, как показано на рис. 10.

Вычерчивание деталей надо начинать с проведения осевых и центровых линий, являющихся основой чертежа. С их помощью удобно строить симметричные изображения, откладывая от этих линий размеры, по которым вычерчивают контуры предмета.

Штрихпунктирная с двумя точками тонкая линия показывает линии сгиба на развертках и крайние положения подвижных предметов. Длина штрихов от 5 до 30 мм, расстояние между ними от 4 до 6 мм.

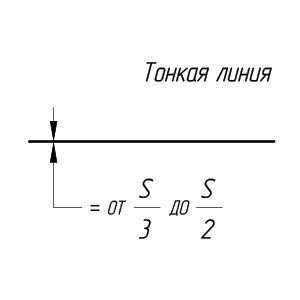
Сплошная тонкая линия. Кроме перечисленных выше линий, на рис. 9 помечены надписями размерные и выносные линии. Выносные линии служат для связи между изображением и размерными линиями, проведенными вне контура. Для размерных и выносных применяют линию, называемую сплошной тонкой, толщина которой должна находиться в пределах от s/3 до s/2.

1. Линии чертежа

Выносные линии должны выходить за концы стрелок размерной линии примерно на 1-5 мм.

Сплошные тонкие линии применяют также для штриховки в сечениях.

Все перечисленные сведения о линиях даны в табл. 1, которую для справок следует переписать в свою рабочую тетрадь.

Ответьте на вопросы?

1. В зависимости от чего берется толщина штриховой, штрихпунктирной тонкой и сплошной тонкой линий? Чему будет равна толщина линий, если толщина сплошной толстой основной линии взята 1,2 мм?

2. Каково основное назначение следующих линий: сплошной толстой основной, штриховой, штрихпунктирной тонкой, сплошной тонкой?

4. Чему равна длина штрихов и расстояние между ними в штриховых линиях? В штрихпунктирных тонких линиях?

Задания к § 2

Упражнение 6

На рис. 10 дан чертеж детали. Цифрами отмечены различные линии. Составьте в рабочей тетради следующую таблицу и заполните ее.

Рис. 10. Задание для упражнений

Упражнение 7

На рис. 11 и 12 даны примеры правильного и неправильного проведения штриховых и штрихпунктирных тонких линий. В чем недостатки проведения линий в примерах 1, 2, 3, 4?

Рис. 12. Примеры проведения штрихпунктирных линий

Правильно	Неправильно
1 —-—-—
—-—-—-—	2 —-—-—
—-—-—-—	3 —-—-—
4 —-—-—

Упражнение 8

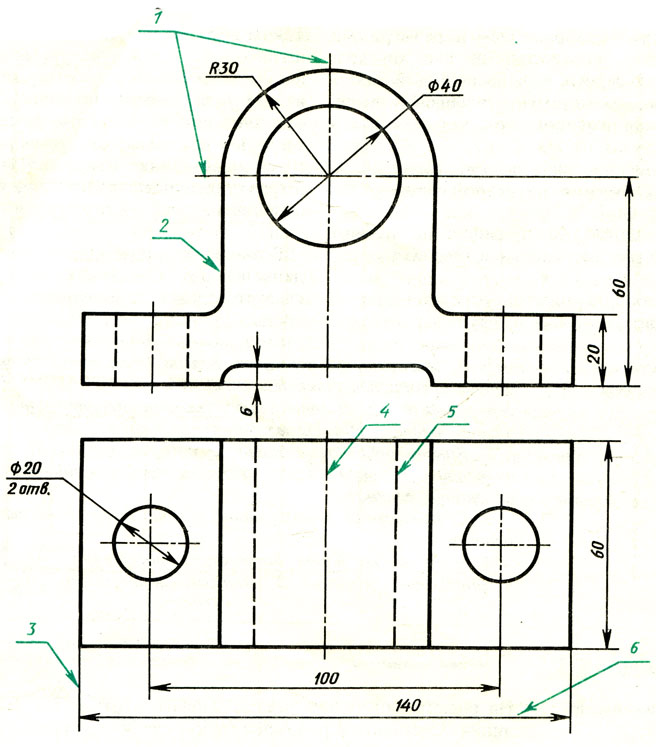
На рис. 13 даны примеры правильного и неправильного взаимного расположения линий. Сравните их. В чем ошибки примеров, помеченных цифрами 1, 2, 3?

Рис. 13. Примеры использования штриховых и штрихпунктирных линий

Упражнение 9

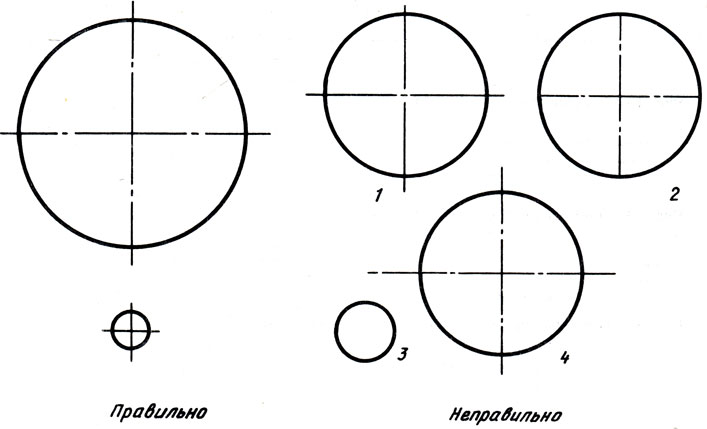
На рис. 14 слева показано, как правильно располагать центровые линии, а справа приведены ошибки, которые часто допускают учащиеся. В чем недостатки изображений, помеченных цифрами 1, 2, 3, 4? Заметьте, что если диаметр окружности на чертеже меньше 12 мм, то центровые линии проводят сплошными.

Рис. 14. Примеры проведения центровых линий

Упражнение 10

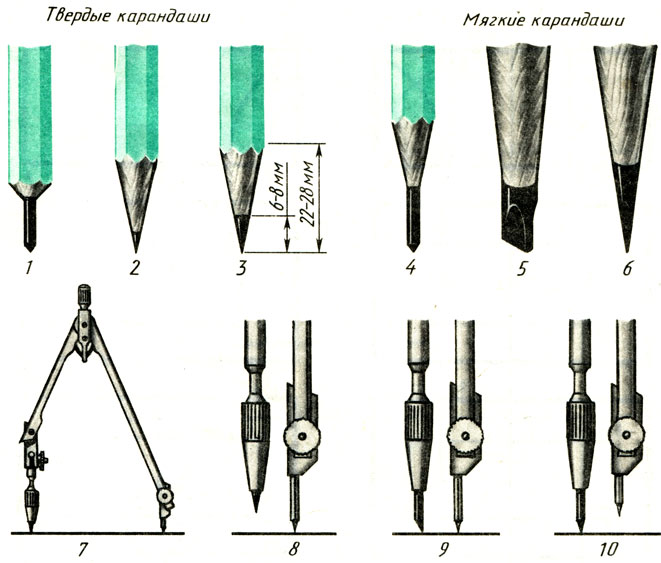
На рис. 15 даны примеры заточки карандашей и подготовки к работе циркулей. Запишите в тетради номера правильно подготовленных к работе карандашей и циркулей.

Рис. 15. Правильная и неправильная подготовка инструмента к работе

Источник

Основные линии чертежа

Линия является основным элементом чертежа. Различаются линии между собой по типу и по толщине.

Толщина сплошной основной линии S должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения, а также от формата чертежа.

Сплошная толстая линия применяется для изображения видимого контура предмета, контура вынесенного сечения и входящего в состав разреза.

Сплошная тонкая линия применяется для изображения размерных и выносных линий, штриховки сечений, линии контура наложенного сечения, линии–выноски, линии для изображения пограничных деталей («обстановка»).

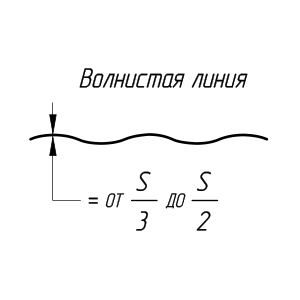
Сплошная волнистая линия применяется для изображения линий обрыва, линии разграничения вида и разреза.

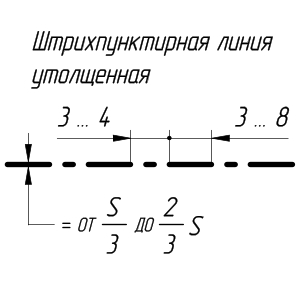
Штрихпунктирная утолщенная линия применяется для изображения элементов, расположенных перед секущей плоскостью («наложенная проекция»), линий, обозначающих поверхности, подлежащие термообработке или покрытию.

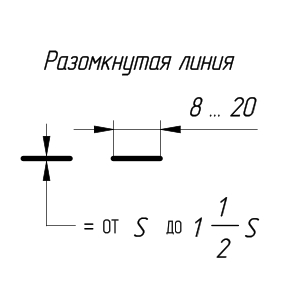
Разомкнутая линия применяется для обозначения линии сечения. Длина штрихов берется 8. 20 мм в зависимости от величины изображения.

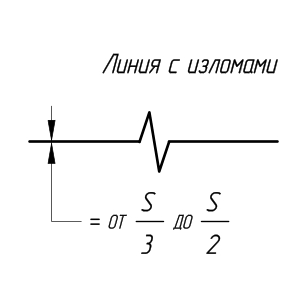
Сплошная тонкая линия с изломами применяется при длинных линиях обрыва.

Штрихпунктирная линия с двумя точками применяется для изображения деталей в крайних или промежуточных положениях; линии сгиба на развертках.

Источник

Линии
(ЕСКД ГОСТ 2.303-68)

Наименование, начертание, толщина линий по отношению к толщине основной линии и основные назначения линий установлены ГОСТ 2.303-68 и должны соответствовать указанным в таблице 1.

Таблица 1. Наименование, начертание, толщина линий по отношению к толщине основной линии и основные назначения линий

Сплошная толстая основная

Линии перехода видимые

Линии контура сечения (вынесенного и входящего в состав разреза)

Линия контура наложенного сечения
Линии размерные и выносные

Линии для изображения пограничных деталей («обстановка»)

Линии ограничения выносных элементов на видах, разрезах и сечениях

Линии перехода воображаемые

Следы плоскостей, линии построения характерных точек при специальных построениях

Линии разграничения вида и разреза

Линии перехода невидимые

Линии осевые и центровые

Линии сечений, являющиеся осями симметрии для наложенных или вынесенных сечений

Линии, обозначающие поверхности, подлежащие термообработке или покрытию

Линии для изображения элементов, расположенных перед секущей плоскостью («наложенная проекция»)

Длинные линии обрыва

Линии сгиба на развертках

Линии для изображения частей изделия в крайних или промежуточных положениях

Линии для изображения развертки совмещенной с видом

Толщина сплошной линии S должна быть в пределах от 0,5 до 1,4 мм в зависимости от величины и сложности изображения, а также от формата чертежа.

Толщина линий одного и того же типа должна быть одинакова для всех изображений на данном чертеже, вычерчиваемых в одинаковом масштабе.

Длину штрихов в штриховых и штрихпунктирных линиях следует выбирать в зависимости от величины изображения. Штрихи в линии должны быть приблизительно одинаковой длины. Промежутки между штрихами в линии должны быть приблизительно одинаковой длины. Штрих пунктирные линии должны пересекаться и заканчиваться штрихами. Штрих пунктирные линии, применяемые в качестве центровых, следует заменять сплошными тонкими линиями, если диаметры окружности или размеры других геометрических фигур в изображении менее 12 мм.

Специальные назначения линий (изображение резьбы, шлицев, границы зон с различной шероховатостью и т.п.) определены в соответствующих стандартах ЕСКД.

Источник