Что такое основание конуса

Инструменты пользователя

Инструменты сайта

Боковая панель

Стереометрия:

Контакты

Конус

Конусом ( прямым круговым конусом ) называется тело, состоящее из круга ( основания конуса ), точки, не лежащей в плоскости этого круга ( вершины конуса ), и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса.

Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности.

Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности.

Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью.

Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса.

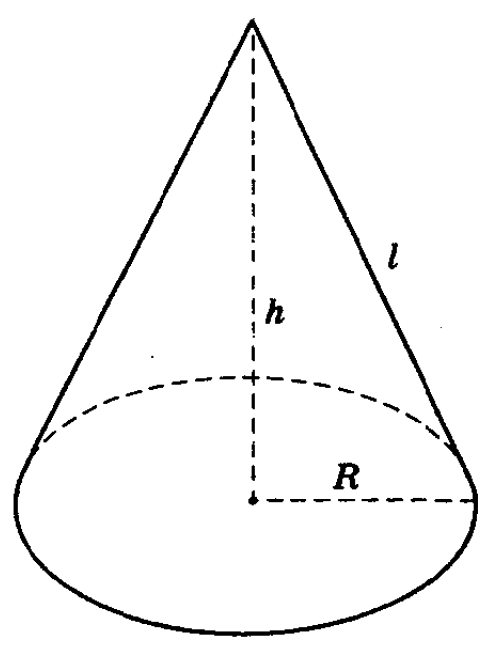
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус.

Круговой конус — конус, у которого в основании круг.

Прямой круговой конус ( просто конус ) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания.

Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса.

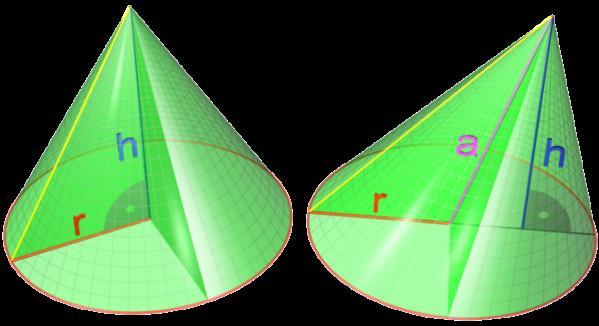
Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания.

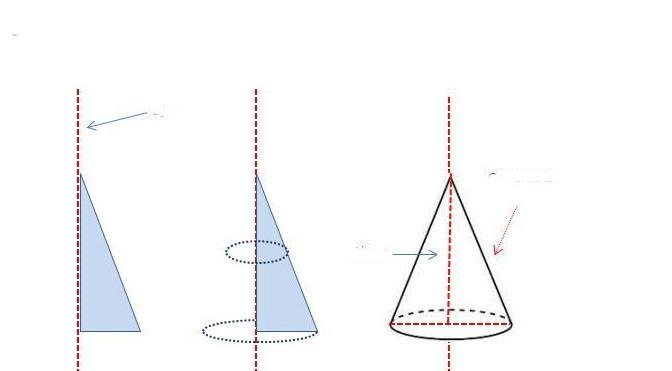
Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет.

Образующие конуса совпадают с образующими конической поверхности.

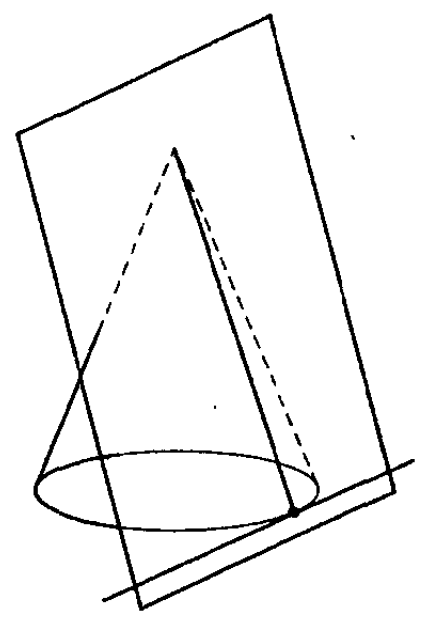
Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. См.Рис.2.

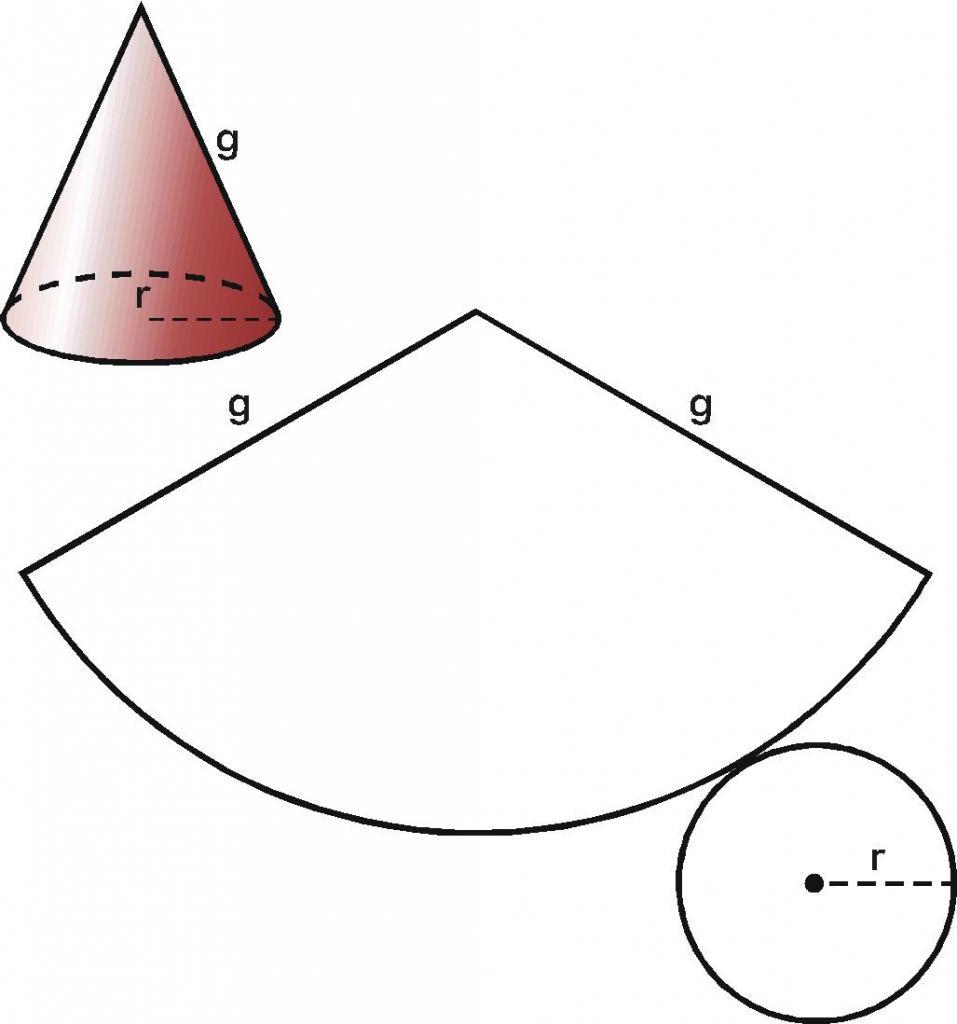
Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.

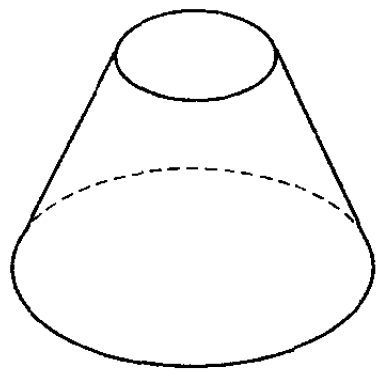
Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3.

Видео-решение.

Инструменты страницы

Записаться на занятия

Источник

Геометрические тела. Конус.

Конус — геометрическое тело в евклидовом пространстве, которое можно получить путем объединения каждого луча, который исходит из одной точки (вершина конуса) и которые проходят через плоскую поверхность.

Бывает, конусом называется часть тела, которая имеет ограниченный объём и которая получена путем объединения каждого отрезка, которые соединяют вершину и точки плоской поверхности. Последняя, в таком случае, является основанием конуса, а конус называется опирающимся на данное основание.

Когда основание конуса является многоугольником – это уже пирамида.

Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Прямой конус – это конус, в котором прямая, которая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.

Прямой круговой конус – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.

Высота конуса – это перпендикуляр, который опущен из вершины конуса на плоскость основания. Основание высоты в прямом конусе совпадает с центром основания.

Ось прямого кругового конуса – это прямая, которая содержит его высоту.

Сечение конуса плоскостью, который проходит через вершину конуса – это равнобедренный треугольник, боковые стороны этого треугольника являются образующими конуса.

Равнобедренным треугольником оказывается и осевое сечение конуса. Это сечение, проходящее через ось конуса.

Плоскость, которая параллельна основанию конуса и которая пересекает конус, отсекает от него конус меньшего размера. Оставшаяся часть является усеченным конусом.

Площадь боковой поверхности правильной n-угольной пирамиды, вписанной в конус:

То есть, площадь боковой поверхности конуса определяют с помощью формулы:

где R — радиус основания конуса, а l — длина образующей.

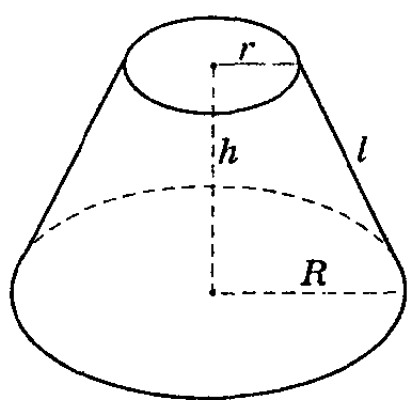
По тому же принципу: для площади боковой поверхности усеченного конуса с радиусами оснований R₁, R₂ и образующей l получаем такую формулу:

Прямой и косой круговой конусы с равным основанием и высотой. Эти тела обладают одинаковым объёмом:

Свойства конуса.

где S — площадь основания, H — высота.

Т.о., каждый конус, который опирается на это основание и имеющие вершину, которая находится на плоскости, параллельной основанию, имеют равный объём, так как их высоты одинаковые.

где α — угол раствора конуса.

а полная площадь поверхности (то есть сумма площадей боковой поверхности и основания), формула:

где R — радиус основания, l — длина образующей.

где S₁ и S₂ — площадь верхнего и нижнего оснований,

h и H — расстояния от плоскости верхнего и нижнего основания до вершины.

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Перечень вопросов, рассматриваемых в теме:

Коническая поверхность – это поверхность, образованная прямыми, проходящими через все точки окружности, и точку, не лежащую в плоскости этой окружности.

Эти прямые – образующие конической поверхности.

Прямая, проходящая через центр окружности, перпендикулярно к плоскости – ось конической поверхности.

Конус– тело, ограниченное конической поверхностью, точкой и кругом.

Ось конической поверхности называется осью цилиндра.

Расстояние от вершины до основания конуса называется высотой конуса, а радиус основания – радиусом конуса.

Сечение – изображение фигуры, образованной рассечением тела плоскостью.

Осевое сечение – вариант сечения, при котором плоскость проходит через ось тела.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 130-133.

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 77-79.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Основные определения

В плоскости 𝛂 построю окружность L с центром в точке О. Проведу прямую ОР перпендикулярно плоскости 𝛂. Соединю точку Р со всеми точками окружности L прямыми линиями. Поверхность, состоящую из этих прямых, называют конической поверхностью, сами прямые называют образующими конической поверхности, точку Р называют вершиной, а прямую ОР – осью конической поверхности.

Ввожу новые понятия конуса, основания конуса, вершины конуса, образующих конуса, боковой поверхности конуса, оси конуса и высоты конуса.

Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом.

Круг называют основанием конуса.

Вершину конической поверхности называют вершиной конуса.

Отрезки образующих, заключённые между вершиной и основанием называют образующими конуса, а образованная ими часть конической поверхности – боковой поверхностью конуса.

Ось конической поверхности называют и осью конуса, а её отрезок, заключённый между вершиной и основанием называют высотой конуса.

Отмечу, что все образующие конуса равны друг другу. Это легко доказать, если рассмотреть различные прямоугольные треугольники, в которых один катет – это высота конуса, а вторыми катетами являются радиусы основания конуса. Тогда образующие, являясь гипотенузами этих прямоугольных треугольников с равными катетами, также будут равны.

2. Сечения конуса различными плоскостями

Это два основных вида сечения конуса, которые изучаются в средней школе на базовом уровне. Следует упомянуть, что существуют и другие сечения конусов, вид которых зависит от расположения секущей плоскости относительно оси.

3. Основные формулы

Формула для вычисления площади боковой поверхности конуса: S_бок=𝛑RL.

Площадь полной поверхности конуса: S_полн=𝛑R(R+L).

Если взять произвольный конус и провести секущую плоскость перпендикулярно его оси, то исходный конус разделится на две части. Верхняя часть представляет собой конус меньших размеров, а оставшуюся часть называют усечённым конусом.

Основание исходного конуса и круг, получившийся в сечении, называют основаниями усечённого конуса.

Отрезок, соединяющий центры оснований, называют высотой усечённого конуса.

Часть конической поверхности, ограничивающая усечённый конус, называется боковой поверхностью усечённого конуса.

Отрезки образующих, заключённые между основаниями, называются образующими усечённого конуса. Отмечу, что все образующие усечённого конуса равны друг другу.

Тогда эта сторона (вокруг которой происходит вращение) будет совпадать с осью конуса и будет его высотой, другая боковая сторона станет образующей и при вращении будет образовывать боковую поверхность, а основания трапеции станут соответственно радиусами верхнего и нижнего оснований усечённого конуса.

5. Формула для вычисления площадей поверхностей усеченного конуса

Примеры и разбор решения заданий тренировочного модуля

1. Найти высоту конуса, если площадь его осевого сечения равна 6, а площадь основания равна 8.

Его высота SO является высотой конуса.

R===OB.

Теперь найдем высоту:

6=SO·OB=SO·.

Отсюда: SO=3

Ответ: 3.

2. Прямоугольная трапеция с основаниями 4 и 7 и меньшей боковой стороной 4 вращается вокруг меньшей стороны. Найдите элементы усеченного конуса.

Радиус меньшего основания

Радиус большего основания

Площадь боковой поверхности конуса

Площадь осевого сечения

Площадь полной поверхности конуса

Трапеция ABCD вращается вокруг стороны AD.

AD – высота усеченного конуса, AD=4.

АВ – радиус меньшего основания, AB=4.

DC – радиус большего основания, DC=7.

Площадь боковой поверхности конуса вычислим по формуле: S_{бок.пов.ук}=π(r+R)L.

Для того чтобы найти площадь боковой поверхности, нужно найти образующую.

Ее найдем из треугольника BHC: BC=5 (это египетский треугольник).

Теперь найдем площадь боковой поверхности.

Площадь боковой поверхности равна 55π.

Осевое сечение представляет собой равнобедренную трапецию с основаниями 8 и 14 и высотой, равной 4.

Так что площадь этой трапеции равна: S=4(4+7)=44.

Для того чтобы найти площадь полной поверхности, нужно к площади боковой поверхности прибавить площади ее оснований.

Источник

Что такое конус: определение. Основание, вершина, высота конуса

Определение фигуры

Предположим, что имеется некоторая плоская замкнутая кривая, например окружность или эллипс. В пространстве выберем некоторую точку, которая не принадлежит плоскости указанной кривой. Теперь соединим ее с каждой точкой на кривой при помощи прямых отрезков. Полученная фигура дает ответ на вопрос о том, что такое конус. На фото ниже показаны три конуса, изготовленные из бумаги.

Вам будет интересно: Подберем рифму к слову «капля»

Исходная замкнутая кривая называется директрисой или направляющей фигуры. Фиксированная точка в пространстве, упомянутая выше, называется вершиной конуса. Прямые отрезки, которые соединяют вершину с точками на директрисе, получили название генератрис, или образующих.

Рассматриваемая фигура образует некоторую поверхность, поэтому объемом не обладает. Если же внутри эту фигуру заполнить каким-либо веществом, то у нее появится некоторый объем. Полученное твердое тело также называется конусом.

Элементы конуса

Вам будет интересно: Абашевская культура бронзового века: локализация, археологические находки

Под элементами фигуры понимают геометрические объекты, из которых она состоит. Зная, что такое конус, можно сказать, что основными его элементами являются следующие:

Виды конуса

Мы узнали, что такое конус. Теперь перейдем к рассмотрению вопроса о том, какие виды фигур бывают.

В зависимости от кривой, находящейся в основании, говорят о конусе круглом, эллиптическом, гиперболическом, параболическом и так далее. Кроме того, фигура может быть прямой и наклонной. Чтобы понять разницу между ними, следует познакомиться с понятием высоты.

В большинстве геометрических задач рассматривают прямой конус с круглым основанием. Далее в статье дадим подробную характеристику этой фигуре.

Как можно получить круглый прямой конус?

В результате описанного способа получения круглого конуса образуется фигура, имеющая радиус основания a и высоту b. Катет b является частью оси конуса, которая проходит через его вершину и центр основания. Гипотенуза исходного треугольника будет генератрисой фигуры.

Схема выше показывает, как можно получить конус, вращая прямоугольный треугольник вокруг одного из катетов.

Линейные характеристики круглого прямого конуса

Фигура образована кругом некоторого радиуса r и конической поверхностью. Пусть высота конуса равна h. Указанные две линейные характеристики являются основными. Их знание позволяет вычислить любые параметры фигуры, например, длину его генератрис, площадь поверхности и объем.

Поскольку рассматриваемая фигура является прямой, то длины всех его генератрис равны между собой. Если обозначить их длину буквой d, тогда формула для ее вычисления будет иметь вид:

Нетрудно догадаться, откуда взялась эта формула. Она является результатом применения теоремы Пифагора к соответствующему прямоугольному треугольнику. Отметим, что генератриса конуса всегда больше радиуса его основания, независимо от значения величины h.

Данное выражение позволяет по двум известным линейным величинам определить третью. Например, если известны d и h, тогда радиус круга в основании будет равен:

Поверхность и объем

S = pi*r2 + pi*r*√(r2 + h2).

Объем конуса произвольного типа рассчитывается по следующей формуле:

Здесь символом So обозначена площадь основания. Заметим, что аналогичная формула и у объема пирамиды. Это совпадение не является случайным, поскольку увеличение числа граней пирамиды до бесконечности переводит ее в конус.

Записанная формула для случая прямого круглого конуса приобретает конкретный вид:

Здесь множитель pi*r2 является площадью основания (круга).

Таким образом, объем прямого конуса, основанием которого является круг, равен одной трети объема цилиндра, имеющего тот же радиус и ту же высоту.

Источник

Геометрические тела. Конус.

Конус — геометрическое тело в евклидовом пространстве, которое можно получить путем объединения каждого луча, который исходит из одной точки (вершина конуса) и которые проходят через плоскую поверхность.

Бывает, конусом называется часть тела, которая имеет ограниченный объём и которая получена путем объединения каждого отрезка, которые соединяют вершину и точки плоской поверхности. Последняя, в таком случае, является основанием конуса, а конус называется опирающимся на данное основание.

Когда основание конуса является многоугольником – это уже пирамида.

Отрезки, которые соединяют вершину конуса и точки окружности основания, называют образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Прямой конус – это конус, в котором прямая, которая соединяет вершину конуса и центр основания, перпендикулярна плоскости основания.

Прямой круговой конус – это тело, которое получено вращением прямоугольного треугольника вокруг его катета как оси.

Высота конуса – это перпендикуляр, который опущен из вершины конуса на плоскость основания. Основание высоты в прямом конусе совпадает с центром основания.

Ось прямого кругового конуса – это прямая, которая содержит его высоту.

Сечение конуса плоскостью, который проходит через вершину конуса – это равнобедренный треугольник, боковые стороны этого треугольника являются образующими конуса.

Равнобедренным треугольником оказывается и осевое сечение конуса. Это сечение, проходящее через ось конуса.

Плоскость, которая параллельна основанию конуса и которая пересекает конус, отсекает от него конус меньшего размера. Оставшаяся часть является усеченным конусом.

Площадь боковой поверхности правильной n-угольной пирамиды, вписанной в конус:

То есть, площадь боковой поверхности конуса определяют с помощью формулы:

где R — радиус основания конуса, а l — длина образующей.

По тому же принципу: для площади боковой поверхности усеченного конуса с радиусами оснований R₁, R₂ и образующей l получаем такую формулу:

Прямой и косой круговой конусы с равным основанием и высотой. Эти тела обладают одинаковым объёмом:

Свойства конуса.

где S — площадь основания, H — высота.

Т.о., каждый конус, который опирается на это основание и имеющие вершину, которая находится на плоскости, параллельной основанию, имеют равный объём, так как их высоты одинаковые.

где α — угол раствора конуса.

а полная площадь поверхности (то есть сумма площадей боковой поверхности и основания), формула:

где R — радиус основания, l — длина образующей.

где S₁ и S₂ — площадь верхнего и нижнего оснований,

h и H — расстояния от плоскости верхнего и нижнего основания до вершины.

Источник