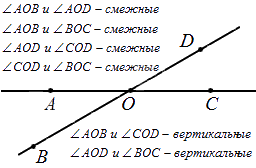Что такое острый угол в математике 4 класс

4 класс. Математика. Угол. Виды углов.

4 класс. Математика. Угол. Виды углов.

Вопросы

Задай свой вопрос по этому материалу!

Поделись с друзьями

Комментарии преподавателя

На этом уроке мы рассмотрим угол и виды углов. Вспомним, что такое луч и как он связан с углом, дадим определение этой геометрической фигуре. Далее рассмотрим разные способы обозначения угла и различные виды углов. Узнаем об инструментах, которые применяются для построения углов. Рассмотрим несколько задач на нахождение углов.

Угол, его понятие, основные элементы. Как обозначать угол?

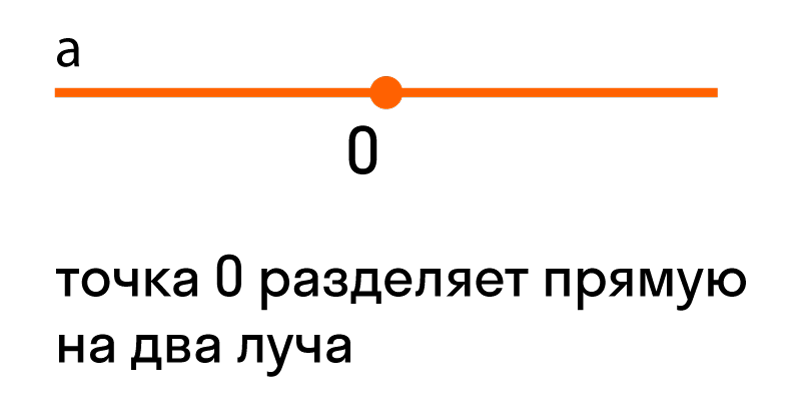
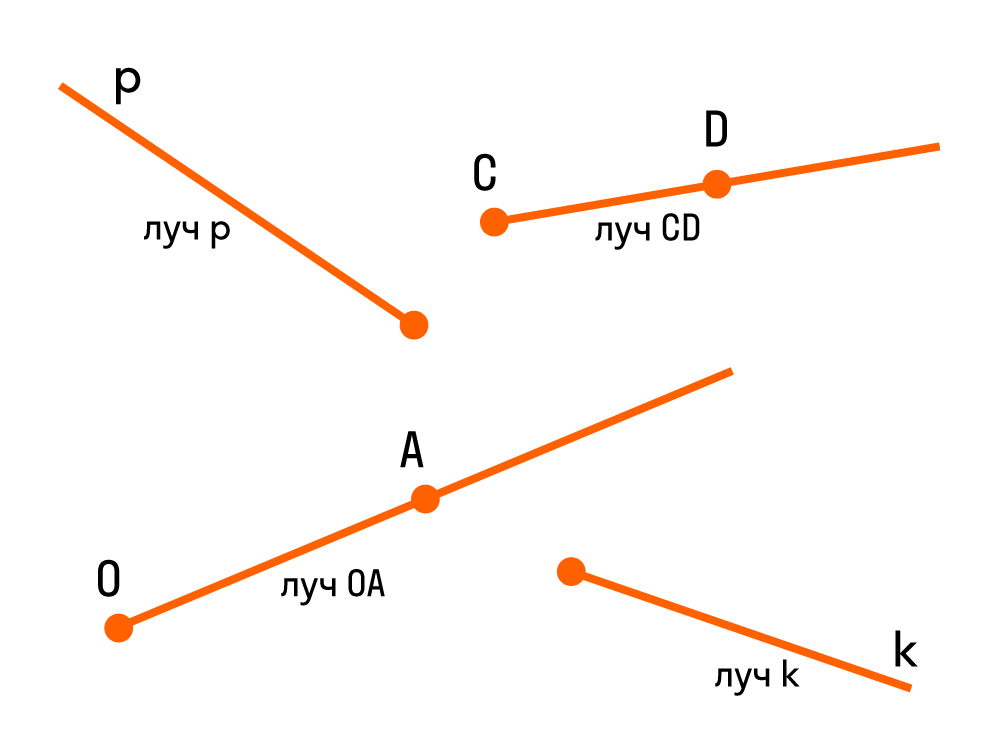
Ранее мы были озна­ком­ле­ны с по­ня­ти­ем «луч». Луч – это часть пря­мой, огра­ни­чен­ная с одной сто­ро­ны точ­кой. На ри­сун­ке можно уви­деть луч с на­ча­лом в точке и луч с на­ча­лом в точке (рис. 1).

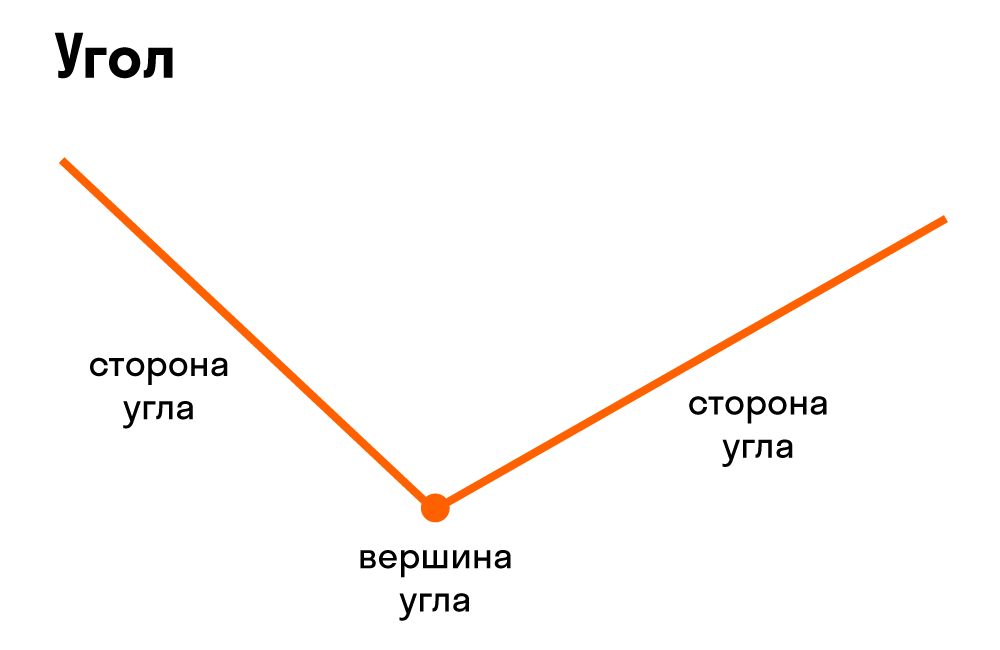
Фи­гу­ра, об­ра­зо­ван­ная двумя лу­ча­ми с одним и тем же на­ча­лом, на­зы­ва­ет­ся углом. Лучи, об­ра­зу­ю­щие угол, на­зы­ва­ют­ся сто­ро­на­ми угла, а их общее на­ча­ло – вер­ши­ной угла (рис. 2).

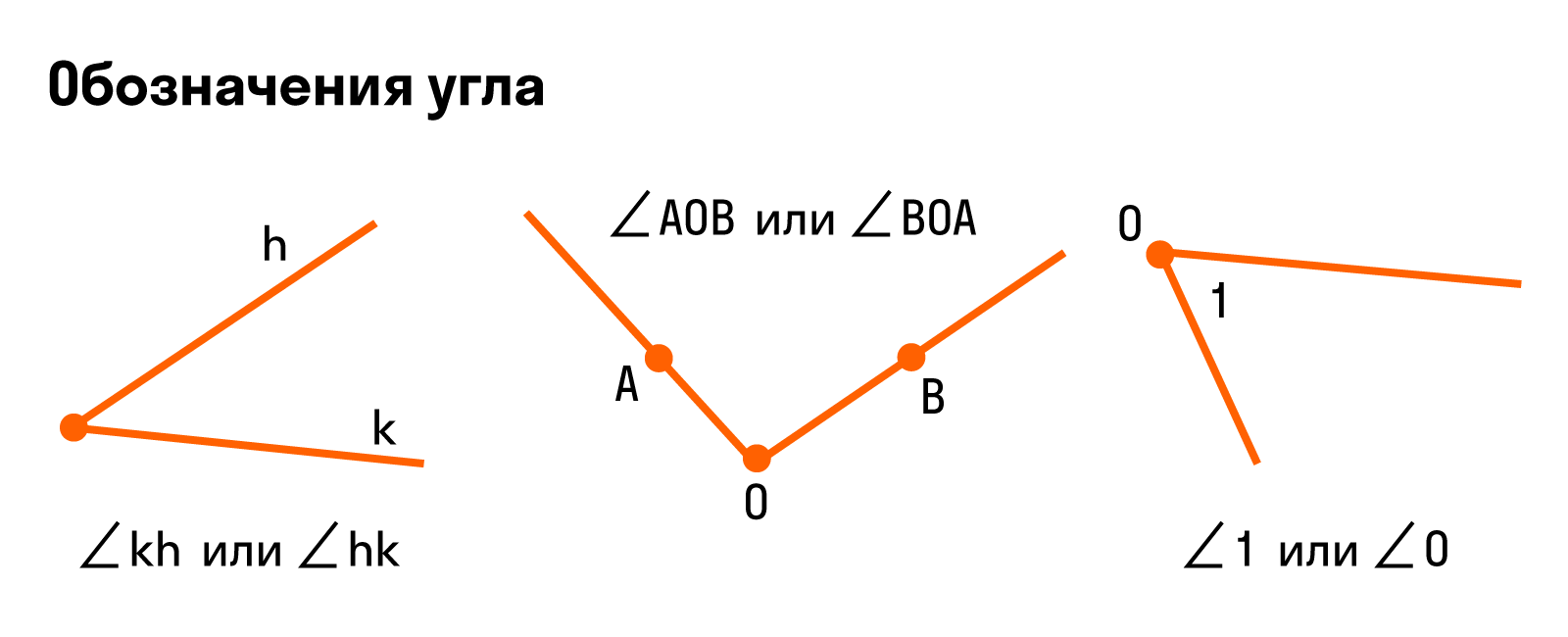
Угол может быть на­зван одной за­глав­ной ла­тин­ской бук­вой по его вер­шине. На рис. 2 можно уви­деть угол и угол . Но углы можно обо­зна­чить и дру­гим спо­со­бом.

Угол мно­го­уголь­ни­ка обо­зна­ча­ют тремя за­глав­ны­ми бук­ва­ми. На­зы­вать угол на­чи­на­ют с буквы, сто­я­щей у одной сто­ро­ны, затем на­зы­ва­ют букву у вер­ши­ны, а за­кан­чи­ва­ют бук­вой у дру­гой сто­ро­ны. На­при­мер, в тре­уголь­ни­ке , угол с вер­ши­ной яв­ля­ет­ся угол (рис. 3) или в об­рат­ном по­ряд­ке – .

В тре­уголь­ни­ке угол с вер­ши­ной – это угол или .

Рис. 3. Углы в тре­уголь­ни­ке

Необ­хо­ди­мо пом­нить, что в се­ре­дине на­зва­ния угла долж­на сто­ять та буква, ко­то­рой обо­зна­че­на вер­ши­на угла.

Ино­гда угол обо­зна­ча­ют малой бук­вой или циф­рой, ставя их внут­ри угла (рис. 4). Между сто­ро­на­ми угла про­во­дят для яс­но­сти дужку.

Рис. 4. Обо­зна­че­ние угла бук­вой или циф­рой

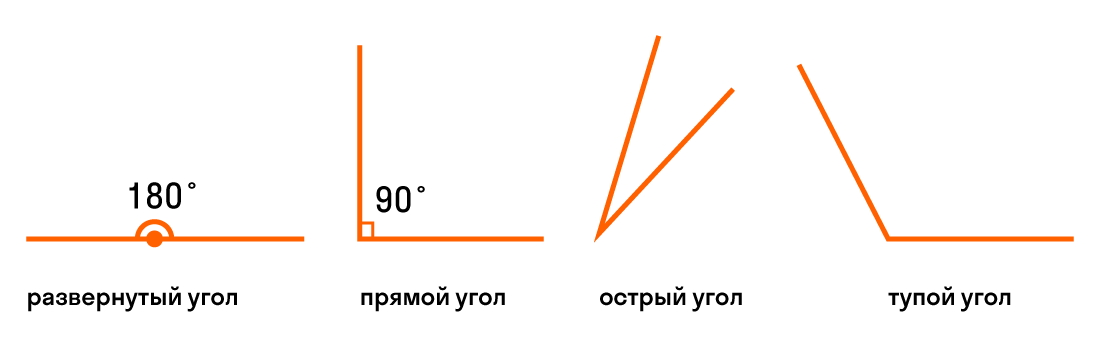
Виды углов

Су­ще­ству­ют раз­лич­ные виды углов.

1. Если сто­ро­ны угла лежат на одной пря­мой, то такой угол на­зы­ва­ют раз­вер­ну­тым. На рис. 6 угол М – раз­вер­ну­тый (умест­но срав­не­ние с раз­вер­ну­тым ве­е­ром).

Рис. 6. Раз­вер­ну­тый угол

2. Пря­мым углом на­зы­ва­ют тот угол, ко­то­рый со­став­ля­ет по­ло­ви­ну раз­вер­ну­то­го угла (рис. 7). На­при­мер, пря­мой угол можно по­лу­чить путем скла­ды­ва­ния бу­ма­ги (если лист сло­жить два­жды).

Для удоб­ства опре­де­ле­ния, пря­мой угол или нет, есть осо­бый ин­стру­мент – пря­мо­уголь­ный тре­уголь­ник, у ко­то­ро­го один из углов – пря­мой (рис. 8).

Рис. 8. Пря­мо­уголь­ный тре­уголь­ник и его при­ме­не­ние

3. Непря­мые углы де­лят­ся на тупые и ост­рые.

Угол, ко­то­рый мень­ше пря­мо­го, – это ост­рый угол (рис. 9).

Рис. 9. Ост­рый угол
Угол, ко­то­рый боль­ше пря­мо­го, но мень­ше раз­вер­ну­то­го угла, – это тупой угол (рис. 10).

Задание

Най­ди­те на чер­те­же пря­мые, тупые и ост­рые углы (рис. 11).

Рис. 11. Ил­лю­стра­ция к за­да­нию

В на­хож­де­нии ре­ше­ния нам по­мо­жет ин­стру­мент – пря­мо­уголь­ный тре­уголь­ник, ко­то­рый будет при­ло­жен к каж­дой из вер­шин тре­уголь­ни­ка путем сов­ме­ще­ния одной из сто­рон. Если он будет сов­па­дать с углом, то этот угол пря­мой. Если угол будет мень­ше пря­мо­го угла ин­стру­мен­та, то этот угол ост­рый. А если же угол боль­ше пря­мо­го угла ин­стру­мен­та – то это тупой угол.

Пря­мые углы:

Тупые углы:

Ост­рые углы: , , ,

Построение 4 прямых углов с общей вершиной на нелинованной бумаге

В по­стро­е­нии 4 пря­мых углов с общей вер­ши­ной на нели­но­ван­ной бу­ма­ге нам по­мо­гут цир­куль и ли­ней­ка.

Сна­ча­ла необ­хо­ди­мо про­ве­сти пря­мую. От­ло­жим на пря­мой про­из­воль­ный от­ре­зок . Про­ве­дем две окруж­но­сти с цен­тра­ми в точке и с ра­ди­у­са­ми, рав­ны­ми длине от­рез­ка .

Обо­зна­чим точки пе­ре­се­че­ния окруж­но­стей и . Про­ве­дем через точки и пря­мую. Точку пе­ре­се­че­ния пря­мых обо­зна­чим бук­вой .

Рис. 12. По­стро­е­ние 4 пря­мых углов с общей вер­ши­ной на нели­но­ван­ной бу­ма­ге

С по­мо­щью пря­мо­уголь­но­го тре­уголь­ни­ка можно про­ве­рить, что все 4 угла с вер­ши­ной в точке – пря­мые. При по­стро­е­нии пря­мых углов на нели­но­ван­ной бу­ма­ге вме­сто окруж­но­стей можно про­во­дить дуги, то есть части окруж­но­сти. При­чем дуги могут быть лю­бо­го ра­ди­у­са, но боль­ше, чем по­ло­ви­на длины от­рез­ка .

Вывод

На этом уроке мы по­зна­ко­ми­лись с по­ня­ти­ем угла и ви­да­ми углов: раз­вер­ну­тым углом, пря­мым углом, тупым углом и ост­рым углом. На­учи­лись стро­ить пря­мые углы на нели­но­ван­ной бу­ма­ге с по­мо­щью цир­ку­ля и ли­ней­ки.

Источник конспекта: http://interneturok.ru/ru/school/matematika/4-klass/tema-3/ugol-vidy-uglov?konspekt

Источник видео: http://www.youtube.com/watch?v=zoj9YcAz2ws

Файлы

Нет дополнительных материалов для этого занятия.

Источник

Что такое угол? Виды углов

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.

Иногда можно встретить обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Что такое вершина и стороны угла:

Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.

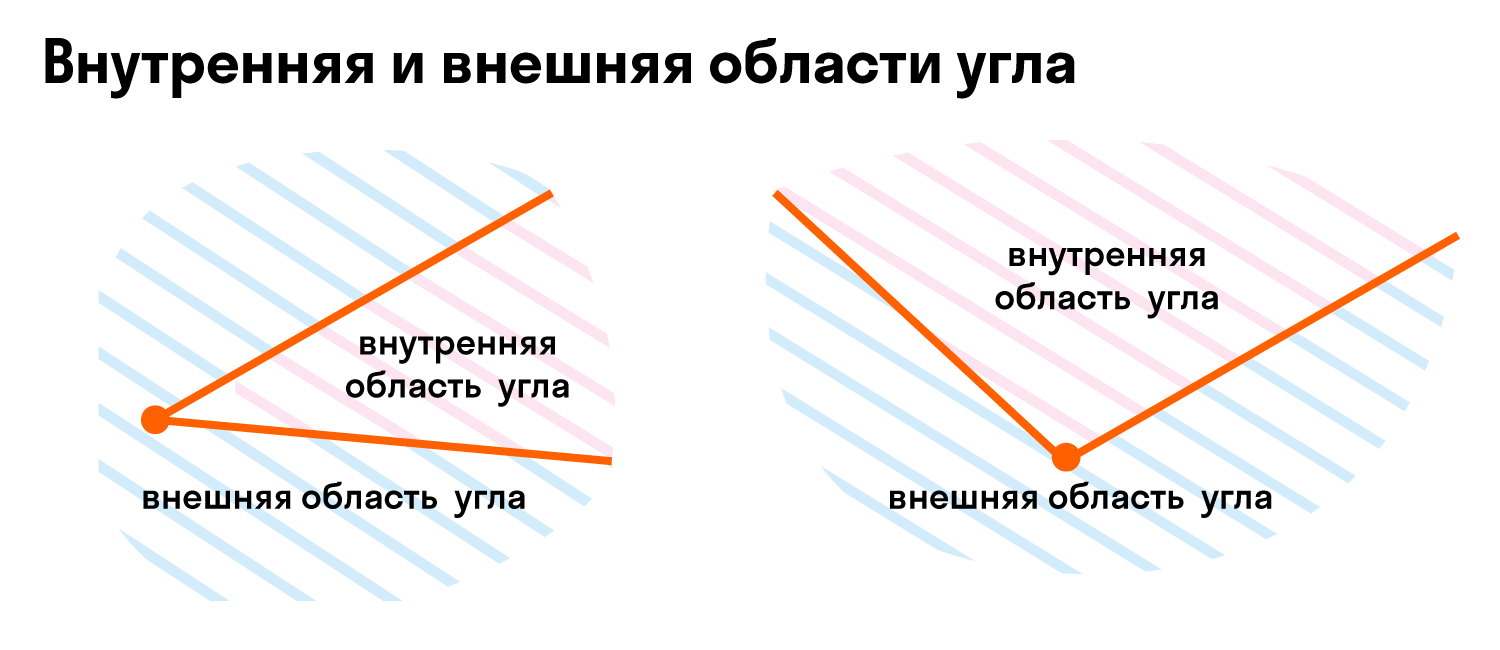
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Единица измерения углов — градусы. Символ для обозначения градуса угла: °.

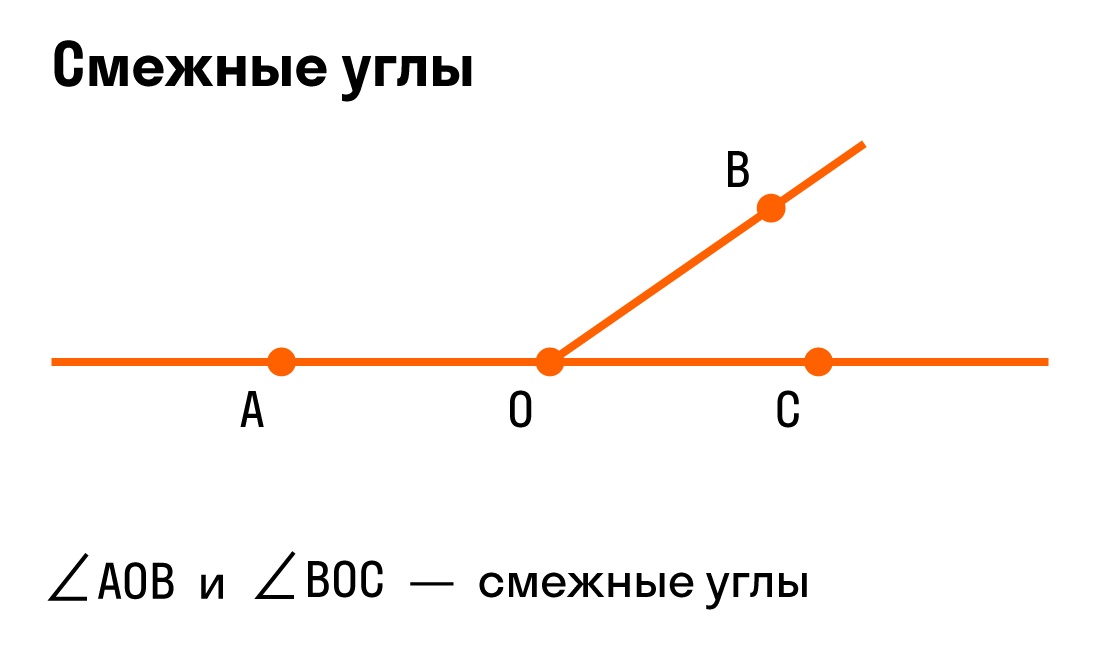
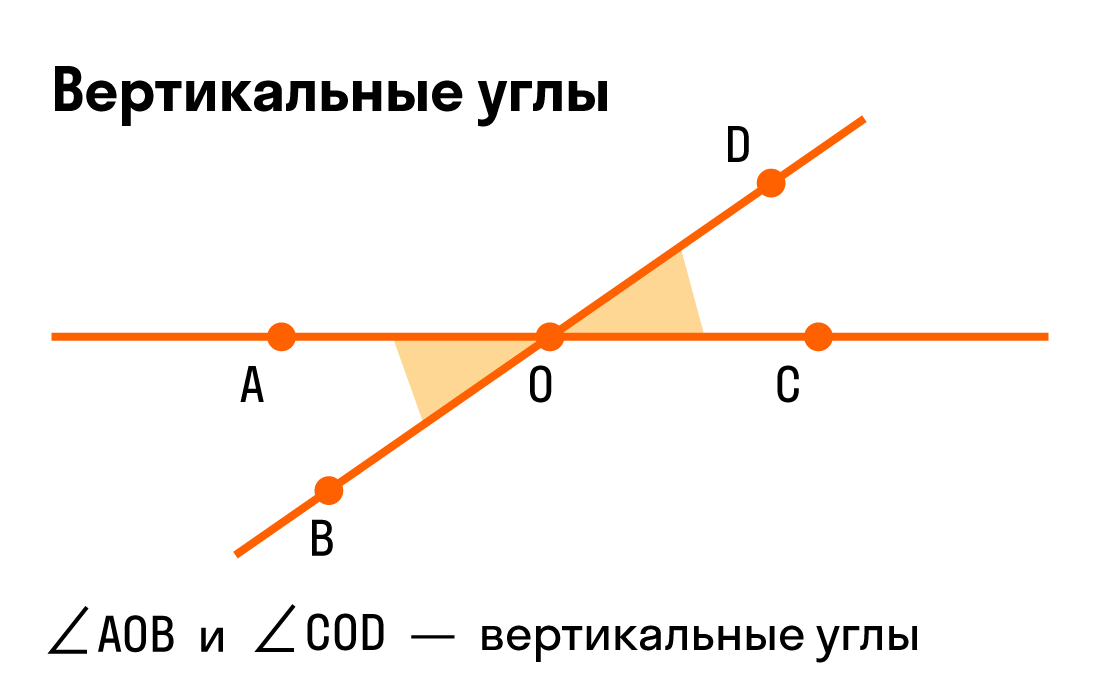
Определение смежных и вертикальных углов

Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.

Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.

При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:

Виды углов

Есть разные типы углов и у каждого своё название:

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

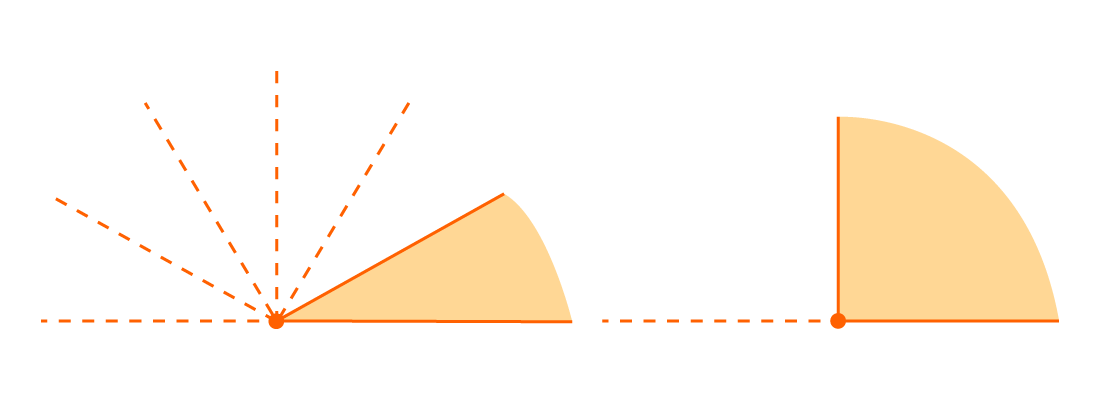
Острый угол — это угол, который меньше прямого угла, то есть

Сравнение углов

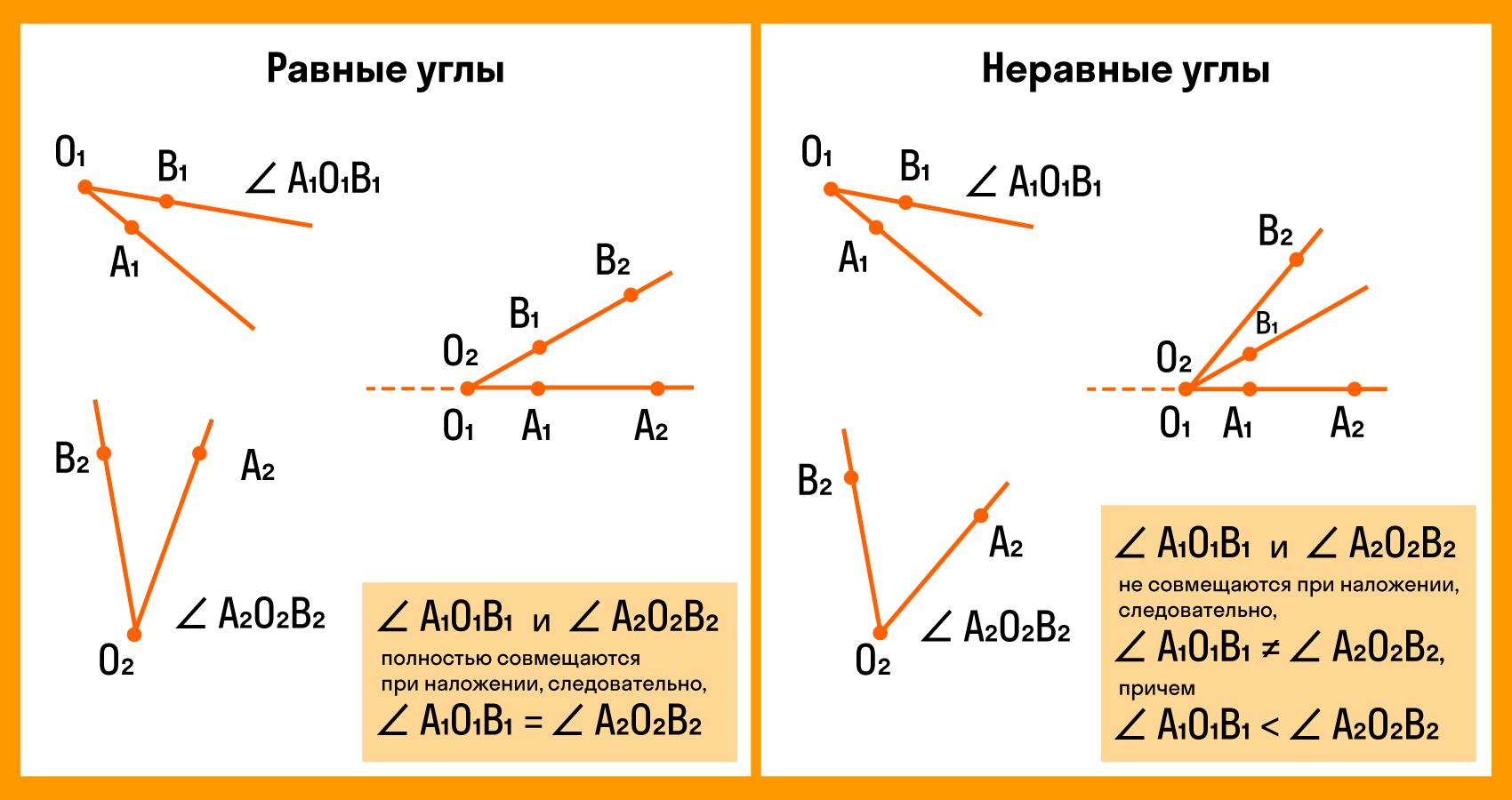
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается — ´.

Секунда — 1/60 часть минуты. Обозначается — ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.

Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

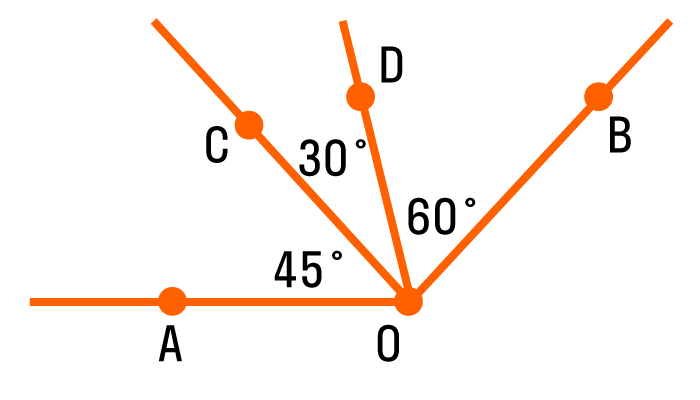
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.

Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.

Равные углы имеют равную градусную меру.

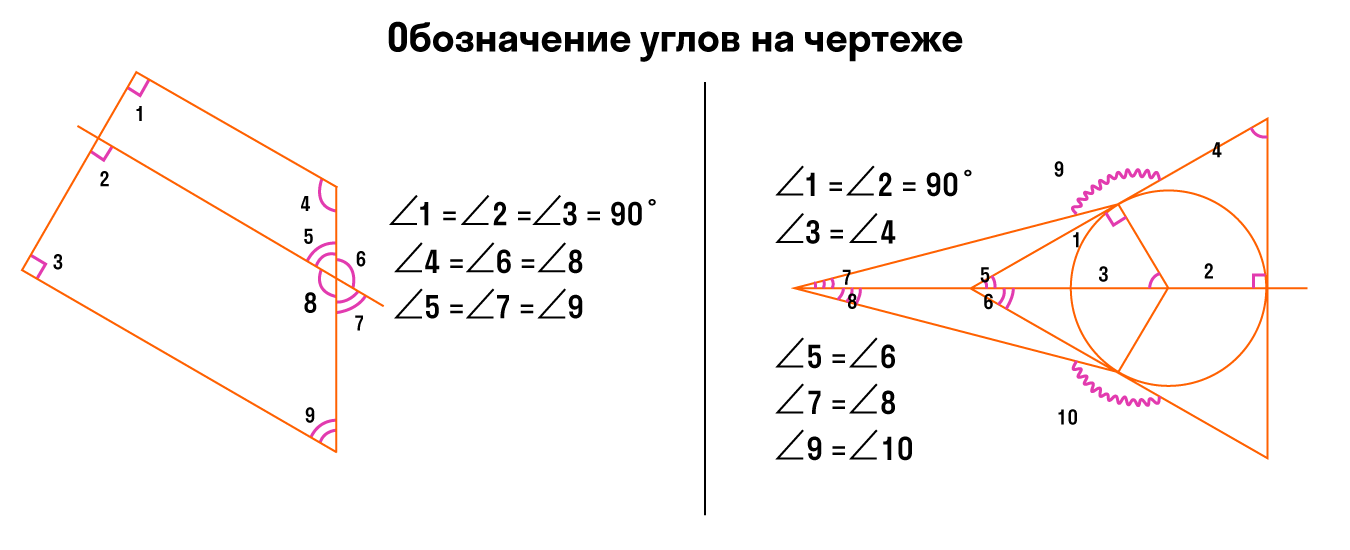
Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:

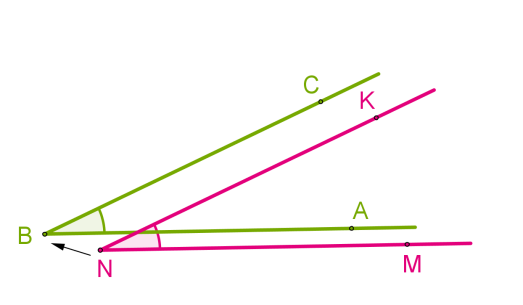
На чертеже отмечены острые, равные и неравные углы.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Источник

Урок математики «Угол. Виды углов» (УМК «Школа России»). 4-й класс

Класс: 4

Вид урока: урок изучения и первичного закрепления новых знаний.

Цель: формирование общего понятия об угле, видах углов.

1. Образовательные:
– Познакомить учащихся с понятием “прямой угол”;
– Сформировать практические навыки определения прямого угла при помощи треугольника и без него;

2. Развивающие:
– Развитие логического мышления, внимания, памяти, пространственного воображения;
– Развитие творческих умений и навыков по теме для успешного выполнения заданий;
– Развитие культуры речи и эмоций учащихся.

– В целях решения задач нравственного воспитания содействовать воспитанию, наблюдательности и любознательности, развитию познавательной активности;
– формированию навыков самостоятельной работы;
– В целях решения задач эстетического воспитания содействовать развитию у учащихся чувства прекрасного.

Оборудование: приложения, листы бумаги, прямоугольники.

I. Организационный момент.

Ну-ка проверь, дружок,
Ты готов начать урок?
Все ль на месте?
Все ль в порядке?
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только лишь оценку “5”.

– Ребята, сегодня мы опять отправимся в путешествие по королевству Геометрия, перед вами жители королевства “Геометрия”.

– Посмотрите на фигуры в каждой рамке. Какая из них лишняя? Почему?

(Учащиеся называют лишние фигуры, обосновывают свой выбор.)

– Разделите все оставшиеся фигуры на две группы. Как это можно сделать?

(Оставшиеся фигуры можно разделить на две группы: линии и многоугольники.)

– Назовите виды линий и многоугольников, известные вам.

(Линии: прямая, ломаная, кривая. Многоугольники: квадрат, трапеция, прямоугольник, четырехугольник, пятиугольник, шестиугольник, многоугольник.)

III. Актуализация знаний. Повторение изученного.

1) Игра “Самый внимательный”.

(Дети указкой показывают треугольники и квадраты.)

IV. Введение в тему урока

– Тему урока вам подскажет кроссворд.

1) Часть прямой, у которой есть начало, но нет конца. (Луч.)

2) Геометрическая фигура, не имеющая углов. (Круг.)

3) Самая маленькая геометрическая фигура. (Точка.)

4) Геометрическая фигура, имеющая форму вытянутого круга. (Овал.)

– Тема нашего урока спряталась по вертикали. Найдите ее. (Угол.)
– А что такое угол? Почему мы будем его изучать? Пригодится ли нам это в жизни?
– Какова же тема нашего урока? Проблема!

V. Сообщение темы и цели урока.

Угол. Виды углов. – На уроке мы познакомимся с разными видами углов, их свойствами, научимся их обозначать буквами и чертить их.

VI. Работа над новым материалом.

1) Игра “Им угол имя подарил”.

– Угол важная фигура. Многим фигурам он помог дать имя. Назовите фигуры.
– Что общего в названиях фигур? Почему первая часть слов везде разная?
– Углы окружают нас и в повседневной жизни. – Обернитесь, рассмотрите наш класс. Приведите свои примеры, где можно найти углы вокруг нас. Люди, каких профессий чаще всего встречаются с углами? (инженер, дизайнер, строитель, архитектор, моряк, астроном, портной и т.д..)

Найдите словарное слово. Как оно пишется? Составьте с ним предложение.

2) Определение угла.

– На листе тетради отметьте точку и обозначьте ее буквой О. Проведите из точки О два луча. На сколько частей лучи разделили плоскость? Меньшую часть заштрихуйте цветным карандашом. Какую фигуру вы заштриховали? (Угол.) Так что же такое угол?

Угол – это геометрическая фигура, образованная двумя разными лучами с общим началом.

3) Обозначение углов.

– Точка О – вершина угла. Угол можно назвать одной буквой, записанной около его вершины. Угол О. Но может быть несколько углов, имеющих одну вершину. Как быть тогда?

– В таких случаях если называть разные углы одной буквой, то будет непонятно, о каком угле идет речь. Что этого не произошло, на каждой стороне угла можно отметить по одной точке, поставить около нее букву и обозначить угол тремя буквами, при этом всегда в середине записывают букву, обозначающую вершину угла. Угол АОВ. Лучи АО и ОВ – стороны угла.

4) Практическая работа. Построение модели прямого угла.

– Углы бывают разные, но сначала мы познакомимся с самым главным углом.

Попробуйте сами из листа бумаги построить угол. (Возьмите лист бумаги. Сложите лист пополам, а потом еще раз пополам. Обведите линии сгиба карандашом.)

– На сколько частей прямые линии разделили плоскость? (На четыре.)
– Сколько углов получилось? (Четыре.)
– Это особенные углы. Может быть, кто-то знает название этих углов? (Эти углы прямые.)
– На пересечении линий сгиба поставьте точку. Обозначьте один прямой угол буквами. Заштрихуйте цветным карандашом его внутреннюю часть.

5) Определение и построение прямого угла.

– Посмотрите на рисунок, я выделила на нем некоторые углы. Вы найдите и покажите только прямые углы.
– Как вы определили? (На глаз.)
– Не всегда удобно определять прямой угол на глаз.
– При помощи чего еще можно определить угол?

Для этого используют линейку-угольник. Как будем определять?

(Чтобы определить прямой угол или нет угла, нужно совместить вершину и одну сторону угла с вершиной и стороной прямого угла на линейке-угольнике.)

– Какой же угол из трех предложенных прямой?
– Почему вы так решили? (Вершина и стороны угла совпали с прямым углом на линейке-угольнике.)

VII. Закрепление пройденного.

– На рисунке видно, что бывают и другие углы не прямые.

Как называется угол больше прямого? (Тупой.)

– Меньше прямого? (Острый.)
– Каждый из углов имеет свое название. Почему они так называются?

*Острый угол – это угол, который меньше прямого. Тупой угол – это угол, который больше прямого. – Какое правило работы важно помнить, при определении вида угла с помощью линейки-угольника?

– Как же определить вид угла?

*Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике.

2.) Построение прямого угла.

– Используя модель прямого угла, определи виды углов и выпиши их номера. (Дети выполняют задание самостоятельно, затем один ученик называет свой вариант ответа, все проверяют работу.)
– С помощью угольника удобно не только определять прямые углы, но главное – строить их. Построим прямой угол, каждый сам назовет его одной или тремя буквами.

(Учитель на доске, а дети в тетрадях строят прямой угол.) – Работа в парах.

3.) Работа в тетради.

– Начертите в тетради острый и тупой угол, подпишите их. Острый угол заштрихуйте зеленым карандашом, а тупой угол синим.

– Чем похожи и чем различаются эти углы?

Похожи: есть вершина, две стороны. Различаются: один больше, другой меньше прямого угла; разные названия.

– С помощью линейки-угольника проверьте работу друг друга в парах. Определить угол сначала “на глаз”, потом проверить с помощью угольника. Чтобы определить вид угла, надо совместить его вершину и сторону соответственно с вершиной и стороной прямого угла на угольнике. Если вторая сторона окажется внутри прямого угла, то угол острый, а если вторая сторона окажется снаружи – то тупой.

VIII. Итог урока. Рефлексия.

а) Положи три спички так, чтобы получились три угла – острый, прямой и тупой. Сделай чертеж.

б) Положи три спички так, чтобы получились три острые и два тупых угла. Сделай чертеж.

3. Сегодня на уроке:

Я узнал …..
Я научился…
Мне понравилось ….
Я бы хотел ….
Знания мне пригодятся…..

IX. Домашняя работа.

Игра “Веселый конструктор”.

– Придумайте и нарисуйте различные предметы, используя круги, овалы, точки, лучи и углы.

Источник