Что такое отсчет в метрологии

Отсчет показаний (средства измерений)

Употребляется в документе:

Отраслевая система обеспечения единства измерений. Термины и определения

Смотреть что такое «Отсчет показаний (средства измерений)» в других словарях:

отсчет показаний средства измерений — отсчет показаний отсчет Фиксация значения величины или числа по показывающему устройству средства измерений в заданный момент времени. Пример. Зафиксированное в данный момент времени по табло бытового электрического счетчика значение, равное… … Справочник технического переводчика

1: — Терминология 1: : dw Номер дня недели. «1» соответствует понедельнику Определения термина из разных документов: dw DUT Разность между московским и всемирным координированным временем, выраженная целым количеством часов Определения термина из… … Словарь-справочник терминов нормативно-технической документации

время — 3.3.4 время tE (time tE): время нагрева начальным пусковым переменным током IА обмотки ротора или статора от температуры, достигаемой в номинальном режиме работы, до допустимой температуры при максимальной температуре окружающей среды. Источник … Словарь-справочник терминов нормативно-технической документации

максимальный уровень — 3.20 максимальный уровень: Максимально допускаемый уровень наполнения резервуара жидкостью при его эксплуатации, установленный технической документацией на резервуар. Источник … Словарь-справочник терминов нормативно-технической документации

метод — метод: Метод косвенного измерения влажности веществ, основанный на зависимости диэлектрической проницаемости этих веществ от их влажности. Источник: РМГ 75 2004: Государственная система обеспечения еди … Словарь-справочник терминов нормативно-технической документации

проверка — 2.9 проверка [аудит]: Систематическая и объективная деятельность по оценке выполнения установленных требований, проводимая лицом (экспертом) или группой лиц, независимых в принятии решений. Источник: ГОСТ Р 52549 2006: Система управления… … Словарь-справочник терминов нормативно-технической документации

МУ 2.6.1.14-2001: Контроль радиационной обстановки. Общие требования — Терминология МУ 2.6.1.14 2001: Контроль радиационной обстановки. Общие требования: 3. Два метрологических понятия связаны со средствами измерений и их практическим применением: погрешность СИ, определяется как отличие показаний СИ от истинного… … Словарь-справочник терминов нормативно-технической документации

схема — 2.59 схема (schema): Описание содержания, структуры и ограничений, используемых для создания и поддержки базы данных. Источник: ГОСТ Р ИСО/МЭК ТО 10032 2007: Эталонная модель управления данными 3.1.17 схема : Документ, на котором показаны в виде… … Словарь-справочник терминов нормативно-технической документации

показание — 4.22 показание (indication): Свидетельство, полученное при неразрушающем контроле. Источник: ГОСТ Р ИСО 3183 2009: Трубы стальные для трубопроводов нефтяной и газовой промышленности. Общие технические условия … Словарь-справочник терминов нормативно-технической документации

Телемеханика — Телемеханика это: наука об управлении и контроле на расстоянии с передачей (по каналу связи) кодированных электрических или радиосигналов, несущих управляющую информацию или данные о состоянии контролируемого объекта. Объектами… … Википедия

Источник

Метрология

Размерности измеряемых величин, шкалы и отсчеты

Понятие о размерности измеряемых величин

При определении размерности производных величин руководствуются следующими правилами:

1. Размерности левой и правой частей уравнений не могут не совпадать, так как сравниваться между собой могут только одинаковые свойства. Объединяя левые и правые части уравнений, можно прийти к выводу, что алгебраически суммироваться могут только величины, имеющие одинаковые размерности.

Итак, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью стеᴨенного одночлена:

Размер измеряемой величины является количественной ее характеристикой. Получение информации о размере физической или нефизической величины является содержанием любого измерения.

Измерительные шкалы и их типы

В теории измерений принято, в основном, различать пять типов шкал: наименований, порядка, разностей (интервалов), отношений и абсолютные.

Шкалы разностей (интервалов) отличаются от шкал порядка тем, что по шкале интервалов можно уже судить не только о том, что размер больше другого, но и на сколько больше. По шкале интервалов возможны такие математические действия, как сложение и вычитание.
Характерным примером является шкала интервалов времени, поскольку интервалы времени можно суммировать или вычитать, но складывать, например, даты каких-либо событий не имеет смысла.

Шкалы отношений описывают свойства, к множеству самих количественных проявлений котоҏыҳ применимы отношения эквивалентности, порядка и суммирования, а следовательно, вычитания и умножения. В шкале отношений существует нулевое значение показателя свойства. Примером является шкала длин.
Любое измерение по шкале отношений заключается в сравнении неизвестного размера с известным и выражении первого через второй в кратном или дольном отношении.

Измерение (сравнение неизвестного с известным) происходит под влиянием множества случайных и неслучайных, аддитивных (прибавляемых) и мультипликативных (умножаемых) факторов, точный учёт которых невозможен, а результат совместного воздействия непредсказуем.

Из приведенной формулы можно выразить значение измеряемой величины Q :

При однократном измерении величины ее значение подсчитывается с учетом поправки:

Значение измеряемой величины при многократном измерении может быть определено из соотношения:

Источник

Измерение. Шкалы измерений

Известное изречение гласит «все познается в сравнении».

Для идентификации объектов и их характеристик во множестве их проявлений требуется большое количество и разнообразие мер. С учетом особенностей измеряемых объектов и задач измерений меры группируют и используют для построения шкал измерений.

Шкала измерений – упорядоченное множество проявлений количественных или качественных характеристик объектов, а также самих объектов. Указанное множество может быть образовано из наименований и обозначений (в том числе в цифровой форме) объектов и их характеристик, а также из значений и числовых значений (для количественных характеристик).

Согласно РМГ 83-2007 [7] «шкала измерений – отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений)». «Измерение – сравнение конкретного проявления измеряемого свойства (величины) со шкалой измерений этого свойства (величины) в целях получения результата измерений (оценки свойства или значения величины)».

Под качественной характеристикой в определении шкалы измерений и далее понимается описание объектов, их свойств и состояний, в словесной форме, в том числе с использованием наименований и обозначений.
Количественная характеристика – характеристика, которая может быть представлена числовым значением, равным отношению количественного содержания этой характеристики к еѐ базовой реализации, называемой единицей измерения.

Шкала наименований – шкала, состоящая из множества наименований (обозначений) объектов или проявлений их характеристик, в соответствии которым поставлено описание объекта (конкретная реализация объекта, его графическое изображение, математическая формула, график и т.п.) или проявлений его характеристик.

Наименование (обозначение) в этом случае рассматривают как обобщенную характеристику объекта или его свойств и состояний. С помощью шкалы наименований устанавливают эквивалентность (равноценность) измеряемого объекта или его характеристик и описания, поставленному в соответствие тому или иному наименованию (обозначению). Это позволяет отнести объект к какой-либо группе или выделить его, путем присвоения индивидуального наименования (обозначения), после чего наименования (обозначения) применяются как идентификаторы объектов (характеристик объектов). При построении шкал наименований могут использоваться числа, но лишь как метки объектов. Примерами таких шкал являются: атласы цветов (до 1000 наименований), запахов (сырой, затхлый, кислый и т.д.), вкуса (чистый, полный, гармоничный и т.д.); множество номеров телефонов, автомашин, паспортов; разделение людей по полу, расе, национальности; классификаторы промышленной продукции, специальностей высшего образования; терминологические справочники и т.п.

Числа, знаки, обозначения, наименования, составляющие шкалу наименований, разрешается менять местами. Для результатов измерений, полученных с использованием этой шкалы, нет отношений типа «больше — меньше», не применимы понятия единица измерения, нуль, размерность. С ними могут проводиться только некоторые математические операции. Например, числа нельзя складывать и вычитать, но можно подсчитывать, сколько раз (как часто) встречается то или иное число.

Оценки экспертов часто осуществляются с использованием шкал порядка. Типичным примером являются задачи ранжирования и классификации промышленных объектов, подлежащих экологическому страхованию.
В отличие от шкалы наименований шкала порядка позволяет не только установить факт равенства или неравенства измеряемых объектов, но и определить характер неравенства в виде суждений: «больше — меньше», «лучше — хуже» и т.п. Однако нельзя утверждать, что землетрясение в 2 балла (лампа качнулась под потолком) ровно в 5 раз слабее, чем землетрясение в 10 баллов (полное разрушение всего на поверхности земли).
Шкалы наименований и порядка, для которых не определены единицы измерений, называют также условными шкалами или не метрическими шкалами.

Абсолютная шкала – шкала числовых значений количественной характеристики. Отличительные признаки абсолютных шкал: наличие естественного нуля и отсутствие необходимости в единице измерений. С использованием абсолютных шкал измеряют коэффициенты усиления, ослабления, амплитудной модуляции, нелинейных искажений, отражения, коэффициент полезного действия и т. п. Результаты измерений в абсолютных шкалах при необходимости выражают в процентах, промилле, байтах, битах, децибелах.
Разновидностью абсолютных шкал являются дискретные (счетные) шкалы, в которых результат измерения выражается числом частиц, квантов, или других объектов, эквивалентных по проявлению измеряемого свойства. Например, шкалы для электрического заряда ядер атомов, числа квантов (в фотохимии), количества информации. Иногда за единицу измерений (со специальным названием) в таких шкалах принимают какое-то определенное число частиц (квантов), например один моль – число частиц, равное числу Авогадро.
Абсолютная шкала, диапазон значений которой находится в пределах от нуля до единицы (или некоторого предельного значения по спецификации шкалы) называют абсолютной ограниченной шкалой.

Шкалы разностей (интервалов), отношений и абсолютные классифицируют как метрические или физические шкалы. Эти шкалы допускают логарифмическое преобразование, часто применяемое на практике, что приводит к изменению типа шкал. Такие шкалы называют логарифмическими. Практическое распространение получили логарифмические шкалы на основе применения систем десятичных и натуральных логарифмов, а также логарифмов с основанием два.

Практически реализация шкал измерений достигается путем стандартизации как самих шкал и единиц измерений, так и, при необходимости, способов и условий (спецификаций) их однозначного воспроизведения.
Измерение с помощью шкал заключается в установлении соответствия объекта или его характеристики отметке на шкале измерений. После чего объекту измерений приписывают количественную или качественную определенность, соответствующую выявленной отметке шкалы.

Источник

Основной постулат метрологии – отсчет – является случайным числом

Шкалы измерений.

Получение информации о размере ФВ является содержанием любого измерения. Количественной характеристикой любого измерения является размер физической величины. Чтобы уяснить, что понимается под измерение в метрологии, рассмотрим типы шкал, на основе которых формируется представление об объекте. В теории измерения принято различать пять типов шкал: шкалы наименований, порядка, разностей (интервалов) и отношений.

Шкала наименований основана на приписывании объекту цифр или знаков, играющих роль простых имен. Примером такой шкалы является распространенная классификация (оценка) цвета по наименованиям (атласы цветов содержат до 1000 наименований).

Шкалы порядка – расположенные в порядке возрастания или убывания размеры измеряемой величины. Полученный при этом упорядоченный ряд называется ранжированным рядом, а саму процедуру – ранжированием. По шкале порядка сравниваются между собой однородные объекты, у которых значения интересующих свойств неизвестны. Поэтому ранжированный ряд может дать ответ на вопросы типа «что больше или меньше» или «что лучше или хуже». Более полную информацию – на сколько больше или во сколько хуже шкала порядка дать не может. Очевидно, что назвать измерением процедуру оценивания свойств объекта по шкале порядка можно только с большой натяжкой. Результаты оценивания по шкале порядка не могут подвергаться никаким арифметическим действиям. Для облегчения измерений по шкале порядка некоторые точки могут быть зафиксированы в качестве реперных (опорных). Примерами таких шкал являются: знания студентов по баллам, землетрясения по 12-бальной шкале, сила ветра по шкале Бофорта, твердость по шкале Мооса. Основным недостатком таких шкал является полное отсутствие уверенности в том, что интервалы между выбранными реперными точками являются равновеликими, а следовательно, по такой шкале нельзя вычислить единицу величины и оценить ее погрешность.

Шкалы разностей (интервалов) отличаются от шкал порядка тем, что по шкале интервалов можно судить не только о том, что размер больше другого, но и на сколько больше. Характерным примером является шкала интервалов времени, поскольку интервалы времени можно суммировать или вычитать. Примером шкал интервалов является и шкала температур. На температурной шкале Цельсия за начало отсчета разности температур принята температура таяния льда. Для удобства пользования шкалой интервалов интервал между температурой таяния льда и температурой кипения воды разделен на 100 интервалов – градусов. На температурной шкале Фаренгейта тот же интервал разбит на 180 градусов. Деление шкалы интервалов на равные части позволяет установить единицу физической величины, что позволяет выразить результат измерения в числовой мере и оценить погрешность измерения. По шкале интервалов возможны такие действия как сложение и вычитание. Однако определить во сколько раз одно значение больше или меньше другого невозможно, поскольку по шкале не определено начало отсчета физической величины.

Шкала отношений представляет интервальную шкалу с естественным началом. Примером является шкала длин. Шкала охватывает интервал значений n от 0 до ∞ и в отличие от шкалы интервалов не содержит отрицательных значений. Температурная шкала Кельвина также является шкалой отношений, т.к. в ней за начало температурной шкалы принят абсолютны ноль (более низкой температуры в природе не существует).

Шкала отношений является самой совершенной, наиболее информативной. Результаты измерений по шкале отношений можно складывать между собой, вычитать, перемножать или делить.

Понятие измерения

Прежде чем сформулировать принятое в метрологии определение понятия «Измерения», отметим следующее. Измерять можно лишь свойства реально существующих объектов, отражаемые физическими величинами. Измерение основывается на экспериментальных процедурах, никакие теоретические рассуждения и математические расчеты сами по себе не могут классифицироваться как измерения. Для проведения измерительного эксперимента необходимы особые технические средства – средства измерений. С учетом этих положений принято следующее определение:

Измерение – нахождение значения ФВ опытным путем с помощью специальных технических средств. Изме­рением какой-либо физической величины является операция, в результате которой определяется, во сколько раз измеряе­мая величина больше или меньше соответствующей величины, принятой за единицу.

Основной постулат метрологии – отсчет – является случайным числом.

Несмотря на то, что измерения непрерывно развиваются, их метрологическая суть остается без измерения и сводится к уравнению измерения

где Q—значение физической величины, U—единица фи­зической величины, п — размер физической величины.

Уравнение (1) является основным уравнением измерения. Правая часть его называется результатом измерения, который всегда является размерной величиной и состоит из единицы физической величины U, имеющей свое наименование, и числа п., показывающего, сколько раз данная единица содержится в измеряемой физической величине.

Виды измерений.

Для изучения метрологии как науки об измерениях рассмотрим классификацию измеренийпо различным признакам. Классификация не является самоцелью, она диктуется потребностями теории и практики. Целесообразность классификация, т.е. подразделение этого понятия на группы, обуславливается удобством при разработке методик выполнения измерений и обработки результатов. Измерения могут быть классифицированы по ряду признаков.

Можно выделить следующие виды измерений

1. По характеру зависимости измеряемой величины от времени измерения подразделяются на:

1.1 Статические, при которых измеряемая величина остается постоянной во времени, например, измерение размеров тела.

1.2. Динамические– в процессе которых измеряемая величина изменяется и является непостоянной во времени. Это проявляется при измерении переменной физической величины в виде отставание показания средства измерения от истинного значения величины в каждый момент времени. Это зависит от инерционных свойств (механических, тепловых, электрических) средства измерения, а также от скорости изменения самой измеряемой величины. Примеров является измерение пульсирующих давлений, вибраций.

2. По способу получения результата, что является целью любого измерения подразделяются на прямые, косвенные, совокупные, совместные. Это также называется видамиизмерений.

Типичным примером совокупных измерений является определение номинальных величин масс отдельных гирь по образцовой величине массы какой либо гири. Например, с помощью совокупных измерений можно провести калибровку гирь массой 1, 2, 3, и 5 кг по одной образцовой гире с действительной массой 1 кг. Допустим также, необходимо измерить размеры физических величин Х1, Х2 и Х3, но мы не имеем устройства, которое дало бы возможность измерить непосредственно указанные величины, но располагаем устройствами, которые позволяют измерить суммы любых дух из указанных величин. Тогда, измеряя сочетания величин, получим следующие уравнения

Х1+Х2= А; Х1+Х3=В; Х2+Х3=С,

Где А, В, С – результаты измерений сочетаний. Искомые величины получаются путем решения указанных уравнений.

Примером могут служить измерения, при которых электрическое сопротивление при температуре и температурные коэффициенты и измерительного сопротивления (резистора) находятся по данным прямых измерений сопротивления резистора при разных температурах t. Уравнение зависимости сопротивления от температуры имеет вид:

(2)

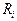
где

Непосредственно измеряются величины и затем при решении системы уравнений находятся величины и . Если n>3, система уравнений решается специальными способами, например, способом решения наименьших квадратов.

Совместные измерения получают все более широкое распространение. Они применяются, например, для анализа сложных, многокомпонентных смесей. Границы применения этого вида измерений особенно расширились с развитием средств вычислительной техники.

3. По условиям, определяющим точность результата:

3.1.Измерения с максимально возможной точностью. Это прежде всего эталонные измерения, связанные с максимально возможной точность воспроизведения установленных единиц ФВ, измерения значений физических констант.

3.2. Контрольно-поверочные измерения – погрешность которых с определенной вероятностью не должна превышать заданное значение. К ним относятся измерения, выполняемые лабораториями государственного надзора и заводскими измерительными лабораториями.

3.3. Технические измерения – погрешность результата которых определяется характеристикой средств измерения. Примерами могут служить измерения, выполняемые в процессе производства на предприятиях.

4. По способу выражения результатов измерений различают:

4.1. Абсолютные измерения – основанные на прямых измерениях величины или использовании значений физических констант, например, измерение значение длины штангенциркулем или микрометром, силы электрического тока в амперах, ускорения свободного падения.

4.2. При относительных измерениях величину сравнивают с одноименной, играющей роль единицы, например, измерение относительной влажности воздуха.

5. По количеству измерительной информации измерения бывают:

5.1. Однократные – это одно измерение одной измеряемой величины. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями.

5.2. Многократные измерения – измерение каждой ФВ более чем один раз.

Методы измерений

Измерения классифицируют также пометодам измерения,которые призваны повысить точность и достоверность полученных результатов.

Любое сложное или простое измерение основано на определенном принципе, т.е. на совокупности физических законов, закономерностей и явлений, используемых при измерении.

Таким образом, принцип измерения показывает на основе использования какого физического закона, закономерности или явления осуществляется преобразование входной ФВ в результат измерения, т.е. получается искомое значение измеряемой величины. Такие преобразования в ходе измерений необходимы очень часто, т.к. во многих случаях непосредственно измерение величин затруднительно, громоздко, а в ряде случаев и невозможно.

Так, например, измерения температуры могут быть осуществлены с помощью использования эффекта объемного теплового расширения тел; измерения массы взвешиванием, т.е. измерением силы тяжести, пропорциональной массе.

Под методами измерения подразумевается совокупность приемов, принципов и средств измерения.

Можно выделить следующие методы измерений.

1. По способу получения значений измеряемых величин: метод непосредственной оценки и метод сравнения с мерой.

1.1.. Метод непосредственной оценки заключается в определении значения измеряемой величины непосредственно по отсчетному устройству измерительного прибора прямого действия, отградуированного в единицах измеряемой величины. Это наиболее распространенный метод измерения, его реализуют большинство средств измерений, например, измерение напряжения электромеханическим вольтметром.

2.2. Методы сравнения с мерой, или методы сравнения, заключаются в сравнении измеряемой величины с величиной, воспроизведенной мерой. Следовательно, отличительной особенностью этих методов является непосредственное участие мер в процессе измерения. К методам сравнения относятся дифференциальный,, нулевой, замещения и совпадений.

а) Дифференциальный метод заключается в сравнении с мерой, при котором на измерительный прибор воздействует разность между измеряемой величиной и известной величиной, воспроизводимой мерой. Т.о. измеряемая величина сравнивается с мерой и о значении величины Х судят по измеряемой прибором разности ΔХ=Х-Х_М и по известной величине Х_М, воспроизводимой мерой. Следовательно, Х= ΔХ+Х_М. Примером является измерение массы на весах (рис. 1. а).

Рис. 1. Методы сравнения с мерой

При дифференциальном методе не производится полного уравновешивания измеряемой величины. Сочетая в себе часть признаков метода непосредственной оценки, дифференциальный метод может дать весьма точный результат измерений, если измеряемая величина и величина, воспроизводимая мерой, мало отличаются друг от друга. Например, если разность этих двух величин составляет 1% и измеряется с погрешностью 1 %, то тем самым погрешность измерений искомой величины уменьшается до 0,01 %, если не учитывать погрешность меры.

б) Нулевой (компенсационный) метод является разновидностью дифференциального метода и заключается в сравнении с мерой, при котором результирующий эффект воздействия величин на прибор сравнения доводится до нуля. Это контролируется специальным измерительным прибором высокой точности – нуль-индикатором. В данном случае значение измеряемой величины равно значению, которое воспроизводит мера. Высокая чувствительность нуль-индикатора, а также выполнение меры с высокой точностью позволяют получить малую погрешность измерения. Пример нулевого метода – взвешивание на весах, когда на одном плече находится взвешиваемый груз, а на другом – набор эталонных грузов (рис. 1.1, б). Другой пример – измерение сопротивления с помощью уравновешенного моста.

в) метод замещения – в котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание на пружинных весах в два приема. Вначале на чашу весов помещают взвешиваемую массу и отмечают положение указателя весов, затем измеряемую массу замещают массой гирь, подбирая их таким образом, чтобы указатель весов устанавливался в том же положении, что и в первом случае.

г) в методе совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадения отметок шкал. Например, совпадение основной и нониусной отметок шкал в штангенприборах для измерения линейных размеров.

2. В зависимости от измерительных средств,используемых в процессе измерения, различают:

1. Инструментальный метод, основанный на использовании специальных технических средств.

2. Экспертный метод основан на использовании данных нескольких специалистов. Широко применяется в квалиметрии, спорте, искусстве, медицине.

3. Эвристические методы оценки основаны на интуиции.

4. Органолептические методы оценки основаны на использовании органов чувств человека.

Источник