Что такое периметр пример

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

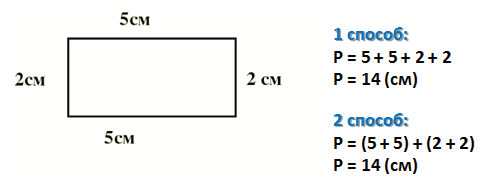
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

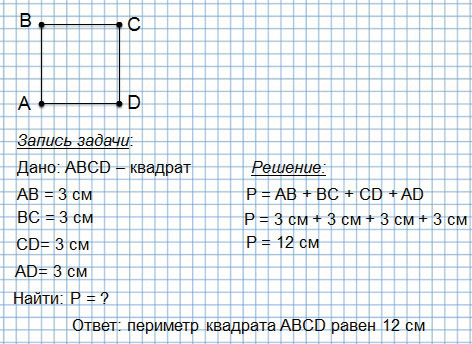
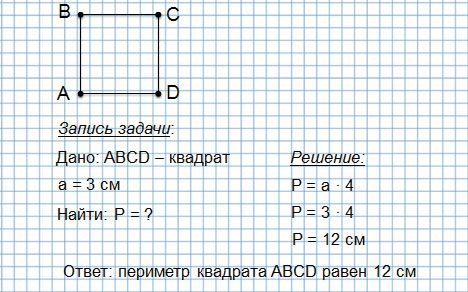
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

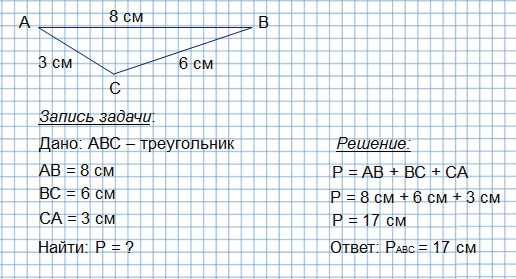
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Как найти периметр фигуры

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник

Что такое периметр геометрической фигуры

В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.

Определение периметра

Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).

Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.

Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:

Формулы периметра распространенных фигур

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Фигура	Название	Пояснение
» data-order=»«>	Квадрат	» data-order=»«>	Прямоугольник	» data-order=»«>	Треугольник	Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см. Пример 2 Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см. Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 8) ⋅ 2 = 28 см. Пример 3 Найдем периметр шестиугольника ниже. P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28. Источник Как найти периметр прямоугольника Основные определения Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°. Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения. Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения. В чем измеряется периметр: Формула нахождения периметра прямоугольника Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы. Когда известны все или две соседние стороны P = a + b + c + d, где a, b, c, d — стороны. Когда известна любая сторона и площадь P = 2 * (a + S : a), где a — сторона, S — площадь. Площадь — это плоскость внутри замкнутой геометрической фигуры. Когда известна любая сторона и диагональ Диагональ — это отрезок, который соединяет противоположные стороны фигуры. Когда известна одна любая сторона и радиус описанной окружности Радиус — отрезок, соединяющий центр и любую точку окружности. Решение задач А теперь практиковаться! 1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр? 2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры? А еще можно вот так: Ответ — такой же, 38 м. 3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см? Источник Периметр многоугольника Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев. В математике периметр обозначают буквой P (пэ). Периметр прямоугольника Например, найдём периметр данного прямоугольника. Этим способом мы пользуемся до тех пор, пока не выучили действие умножение. Мы знаем, что периметр прямоугольника – сумма длин всех его сторон. Формула для подсчета периметра прямоугольника: (a + b) • 2 a – длина прямоугольника b – ширина прямоугольника. Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2. Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см: Периметр треугольника Периметр квадрата Первый способ (когда мы еще не знаем действие умножения): Второй способ (когда мы изучили действие умножения): Поделись с друзьями в социальных сетях: Источник ← Что такое периметр потолка Что такое периметр прямоугольника 1 класс правило примеры → Вам также понравится Магний лекарство для чего 16.08.202316.08.2023 admin 0 Кто такой заместитель директора по увр 25.08.202328.08.2023 admin 0 С чем сочетается зеленый хаки цвет 25.08.202328.08.2023 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email *