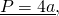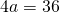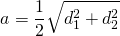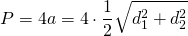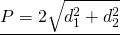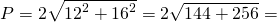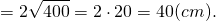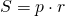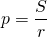Что такое периметр ромба
Нахождение периметра ромба: формула и задачи
В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
Формула вычисления периметра
1. По длине стороны
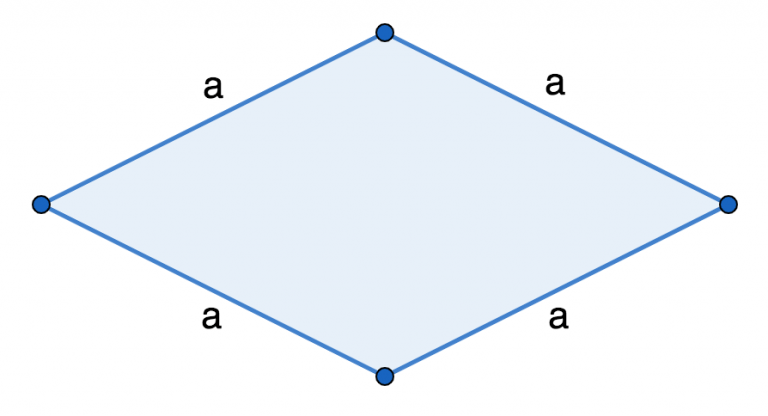
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
2. По длине диагоналей
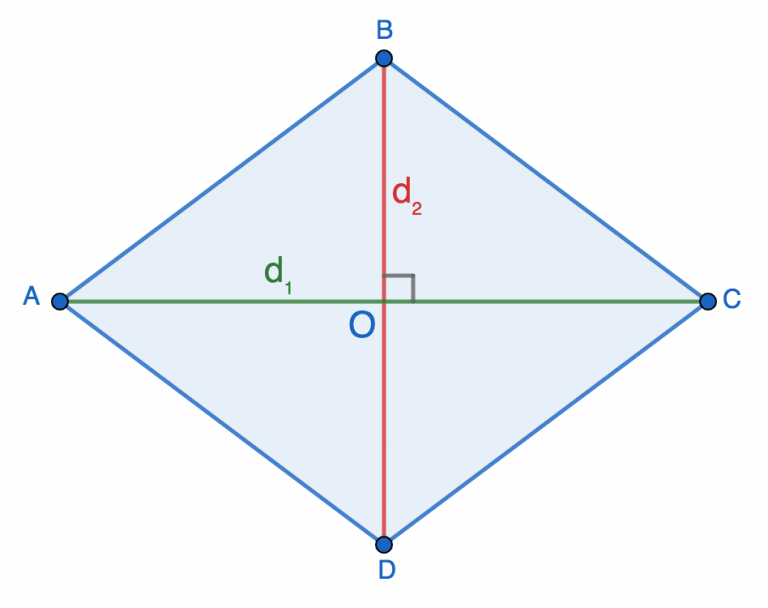
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.е.:
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
AB 2 = AO 2 + OB 2
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
Таким образом, периметр равняется:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
Как найти периметр фигуры
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
Формула нахождения периметра ромба
Периметр ромба
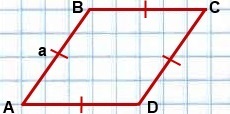
Ромб — это четырехугольник с равными сторонами.
Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы нахождения
Рассмотрим все способы нахождения периметра этой фигуры.
По сторонам
Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:
где a — это сторона ромба.
По двум диагоналям
Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:
где \(d_1\) и \(d_2\) — это диагонали четырехугольника.
Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:
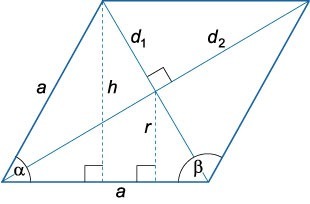
По диагонали и углу
Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:
Далее расчет P будет выглядеть следующим образом:
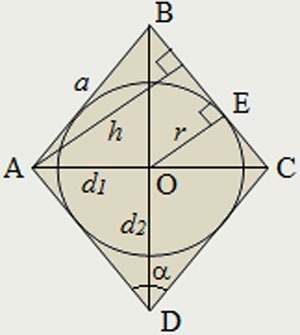
По площади и радиусу вписанной окружности
По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:
где r — это радиус вписанной окружности.
По площади и синусу одного из углов
В этом случае формула расчета суммы всех сторон выглядит так:
Периметр ромба
Как найти периметр ромба, зная его сторону? Как найти периметр ромба по диагоналям? Как, если известен периметр ромба, найти его сторону?
Периметр ромба равен сумме длин всех его сторон.
Поскольку все стороны ромба равны, то формула периметра ромба
где a — длина стороны ромба.
1) Найти периметр ромба со стороной 7 см.
По формуле P=4a имеем: P=4∙7=28 (см).
2) Периметр ромба равен 36 см. Найти его сторону.
По формуле P=4a имеем:
Значит, сторона ромба равна 9 (см).
3) Найти периметр ромба, если его диагонали равны 12 см и 16 см.
Чтобы найти периметр ромба, нужно знать его сторону.
Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям:
Значит, периметр ромба с диагоналями 12 см и 16 см равен
Одна из формул для нахождения площади ромба S связывает радиус r вписанной в ромб окружности и его полупериметр p:
Выразим p через S и r:
Так как P=2p, то приходим к формуле для нахождения периметра ромба через его площадь и радиус вписанной окружности
Ромб. Формулы, признаки и свойства ромба
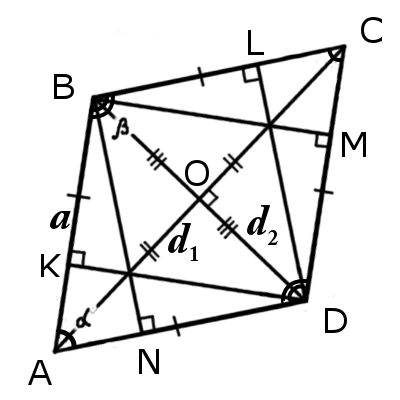 | 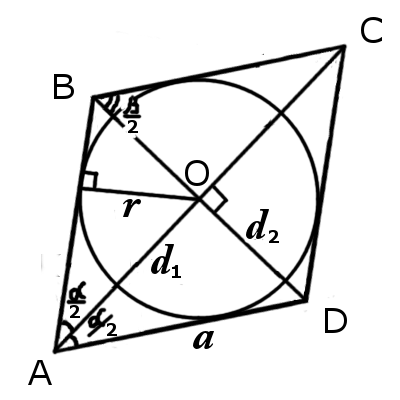 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.