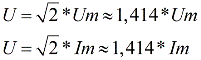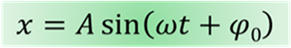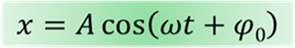Что такое период частота фаза
Основные параметры переменного тока: период, частота, фаза, амплитуда, гармонические колебания
Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока.
Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока.
Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:
Есть и вспомогательные параметры:
Далее рассмотрим все эти параметры по отдельности и во взаимосвязи.
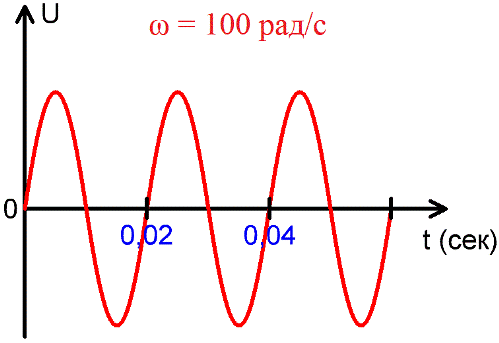
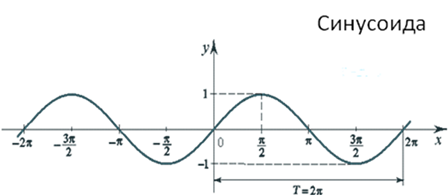
Период — время, в течение которого система, совершающая колебания, проходит через все промежуточные состояния и нале снова возвращается к исходному.
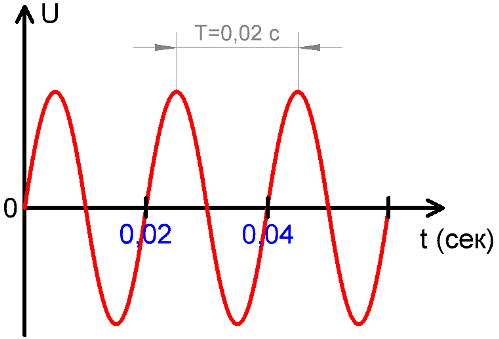
Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.
Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.
Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.
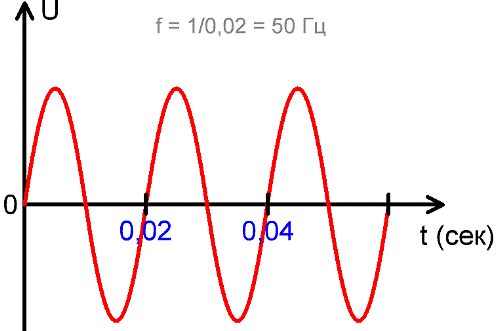
Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.
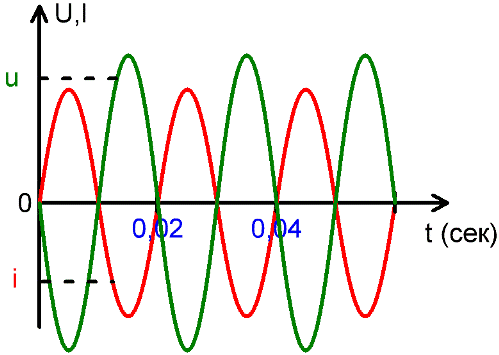
Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.
В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.
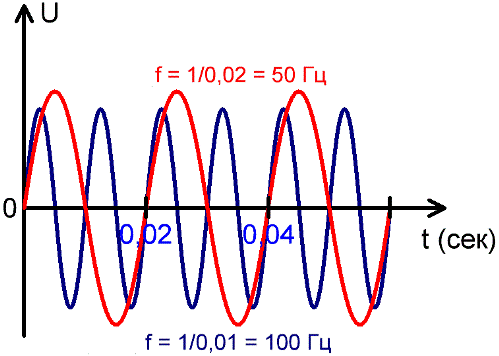
По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.
Угловая частота — число колебаний, совершаемых за 2пи сек.
За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:
Пользоваться числом колебаний на 2пи сек. (а не за 1 сек.) удобно потому, что в формулах, выражающих закон изменения напряжений и токов при гармонических колебаниях, выражающих индуктивное или емкостное сопротивление переменному току, и во многих других случаях частота колебаний n фигурируют вместе с множителем 2пи.
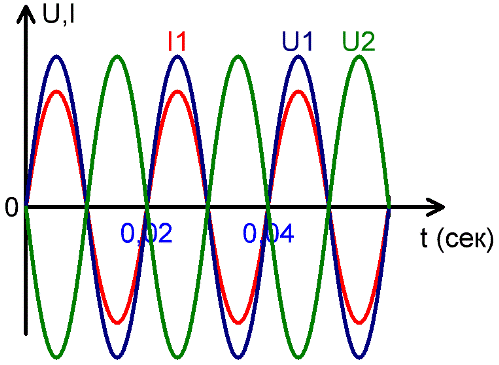
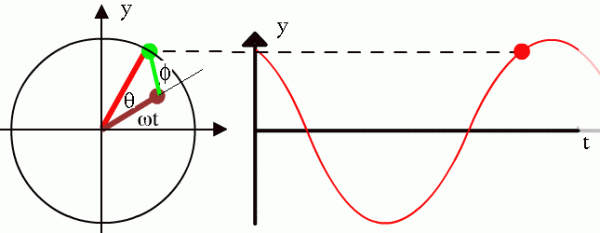
Фаза — состояние, стадия периодическою процесса. Более определенный смысл имеет понятие фаза в случае синусоидальных колебаний. На практике обычно играет роль не фаза сама по себе, а сдвиг фаз между какими-либо двумя периодическими процессами.
В данном случае под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.
На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе измеряется в радианах, долях периода, в градусах.
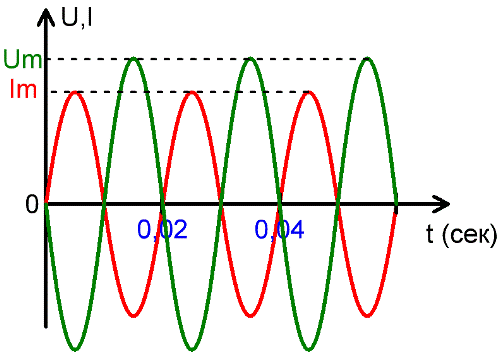
Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.
Амплитуда — наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.
Строго говоря, термин амплитуда относится только к синусоидальным колебаниям, но его обычно (не вполне правильно) применяют в указанном выше смысле ко всяким колебаниям.
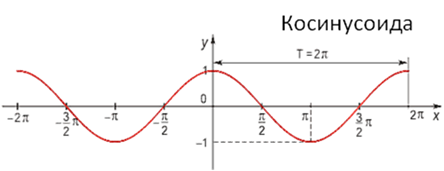
Гармонические колебания — колебания, в которых колеблющаяся величина, например напряжение в электрической цепи, меняется во времени по гармоническому синусоидальному или косинусоидальному закону. Графически представляются кривой — синусоидой.
Реальные процессы могут лишь приближенно быть гармоническими колебаниями. Однако если колебания отражают наиболее характерные черты процесса, то такой процесс считают гармоническими, что существенно облегчает решение многих физических и технических задач.
Движения, близкие к гармоническим колебаниям, совершаются в различных системах: механических (колебания маятника), акустических (колебания столба воздуха в органной трубе), электромагнитных (колебания в LC-контуре) и др. Теория колебаний рассматривает эти различные по физической природе явления с единой точки зрения и определяет их общие свойства.
Графически гармонические колебания удобно представить с помощью вектора, вращающегося с постоянной угловой скоростью вокруг оси, перпендикулярной к этому вектору и проходящей через его начало. Угловая скорость вращения вектора соответствует круговой частоте гармонического колебания.
Векторная диаграмма одного гармонического колебания
Периодический процесс любой формы может быть разложен в бесконечный ряд простых гармонических колебаний с различными частотами, амплитудами и фазами.
Гармоника — гармоническое колебание, частота которого в целое число раз больше частоты некоторого другого колебания, называемого основным тоном. Номер гармоники указывает, во сколько именно раз частота ее больше частоты основного тона (например, третья гармоника — гармоническое колебание с частотой, втрое большей, чем частота основного тона).
Всякое периодическое, но не гармоническое (т. е. отличающееся по форме от синусоидального) колебание может быть представлено в виде суммы гармонических колебаний — основного тона и ряда гармоник. Чем больше рассматриваемое колебание отличается по форме от синусоидального, тем большее число гармоник оно содержит.
Мгновенное значение u и i
Значение ЭДС или тока в конкретный текущий момент времени называется мгновенным значением, они обозначаются маленькими буквами u и i. Но поскольку эти значения все время меняются, то судить о переменных токах и ЭДС по ним неудобно.
Действующие значения I, E и U
Способность переменного тока к совершению какой-нибудь полезной работы, например механически вращать ротор двигателя или производить тепло на нагревательном приборе, удобно оценивать по действующим значениям ЭДС и токов.
Так, действующим значением тока называется значение такого постоянного тока, который при прохождении по проводнику в течение одного периода рассматриваемого переменного тока, производит такую же механическую работу или такое же количество теплоты, что и данный переменный ток.
Действующие значения напряжений, ЭДС и токов обозначают заглавными буквами I, E и U. Для синусоидального переменного тока и для синусоидального переменного напряжения действующие значения равны:
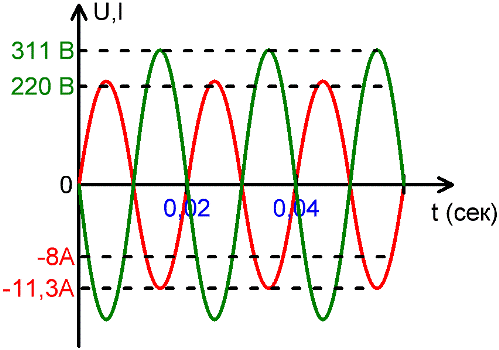
Действующее значение тока и напряжения удобно практически использовать для описания электрических сетей. Например значение в 220-240 вольт — это действующее значение напряжения в современных бытовых розетках, а амплитуда гораздо выше — от 311 до 339 вольт.
Так же и с током, например когда говорят, что по бытовому нагревательному прибору протекает ток в 8 ампер, это значит действующее значение, в то время как амплитуда составляет 11,3 ампер.
Так или иначе, механическая работа и электрическая энергия в электроустановках пропорциональны действующим значениям напряжений и токов. Значительная часть измерительных приборов показывает именно действующие значения напряжений и токов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Частотные характеристики и параметры переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Нормируемые требования к показателям
В РФ требования к качеству работы энергосистемы стандартизированы.
В соответствии с ГОСТ 13109-97 частота в энергосистеме должна непрерывно поддерживаться на уровне f = 50 ± 0,2 Гц, при этом допускается кратковременное отклонение частоты до значения ∆f = 0,4 Гц.
Анализируя зависимость силы тока от частоты, можно сделать вывод, что если подключаемая нагрузка имеет чисто активный характер (к примеру, резистор), то в широком диапазоне сила тока от частоты иметь зависимость не будет. В случае достаточно высоких частот, когда индуктивность и ёмкость подключаемой нагрузки будут характеризоваться сопротивлением, сравнимым с активным, то сила тока будет иметь определенную зависимость от частоты.
Другими словами, при варьировании частоты тока происходит изменение ёмкостного сопротивления, изменение которого, в свою очередь, приводит к изменению тока, протекающего по цепи.
То есть при повышении частоты, снижается ёмкостное сопротивление, и повышается ток, протекающий по цепи.
Математическое выражение зависимости будет иметь следующий вид: I = UCω;
Зависимость при учете активного сопротивления будет определяться следующим выражением: I (ω) = UCω √(R2 • C2 • ω2 + 1).
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
Переменный электрический ток
В английском языке этому термину соответствует выражение alternating current — аббревиатура AC, в энерготехнике как буквенное обозначение используют знак тильда (
). Переменный ток изменяется в периоде по синусоиде. Источниками служат генераторы, вырабатывающие ЭДС посредством электромагнитной индукции. Характеризуется АС следующими параметрами:
В энергетике преимущественно используются трёхфазные сети: 3 отдельных электроцепи с одинаковыми напряжением и частотой при сдвиге φ=120°. От стабильности колебательных движений нуклонов в системе зависит устойчивость и надёжность работы всей энергосети.
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Комментарии
Руслан_98 24.10.2018 18:22 Хорошо объяснили. Разжевали для таких невежд, как я)
Илья_95 10.09.2018 16:27 Спасибо, долго и с длинными периодами я шёл к этой информации. Прояснились понятия периода и фазы наконец, словно получилось добыть первобытный огонь, или догадаться до того, чтобы убрать руку во время того, как вцепился в раскалённую сковородку.
Петя 07.02.2015 17:36 спасибо.надеюсь сдам
Обновить список комментариев
Параметры сетевого напряжения в России[ | ]
Производители электроэнергии генерируют переменный ток промышленной частоты (в России — 50 Гц). В подавляющем большинстве случаев по линиям электропередач передаётся трёхфазный ток, повышенный до высокого и сверхвысокого электрического напряжения с помощью трансформаторных подстанций, которые находятся рядом с электростанциями.
К жилым домам (на сельские улицы) подводятся четырёхпроводные (три фазовых провода и один нейтральный (нулевой) провод)
линии электропередач (воздушные или кабельные ЛЭП) с межфазным напряжением 400 Вольт. Входные автоматы и счётчики потребления электроэнергии, обычно, трёхфазные. К однофазной розетке подводится фазовый провод, нулевой провод и, возможно, провод защитного заземления или зануления, электрическое напряжение между «фазой» и «нулём» составляет 230 Вольт.
В правилах устройства электроустановок (ПУЭ-7) продолжает фигурировать величина 220
, но фактически напряжение в сети почти всегда выше этого значения и достигает 230—240 В, варьируясь от 190 до 250 В[2][
источник не указан 703 дня
].
Номинальные напряжения бытовых сетей (низкого напряжения): Россия (СССР, СНГ)[ | ]
До 1926 года техническим регулированием электрических сетей общего назначения занимался Электротехнический отдел ИРТО, который только выпускал правила по безопасной эксплуатации. При обследовании сетей РСФСР перед созданием плана ГОЭЛРО было установлено, что на тот момент использовались практически все возможные напряжения электрических токов всех видов. Начиная с 1926 года стандартизация электрических сетей перешла к Комитету по стандартизации при Совете Труда и Обороны (Госстандарт), который выпускал стандарты на используемые номинальные напряжения сетей и аппаратуры. Начиная с 1992 года Межгосударственный совет по стандартизации, метрологии и сертификации выпускает стандарты для электрический сетей стран входящих в ЕЭС/ОЭС.
| Переменный ток 50 Гц с разделённой фазой или постоянный ток, двух-/трёхпроводные линии | Трёхфазный переменный ток, 50 Гц | |||||
| 110/220 В | 220/440 В | 3×120 В[р 1] (треугольник) | 127/220 В | 220/380 В | 230/400 В[р 2] | |
| Временные правила ИРТО, 1891[3] | широко используется | запрещен[р 3] | разрешён | запрещен[р 3] | запрещен[р 3] | запрещен[р 3] |
| Дополнение к временным правилам ИРТО от 1898[4] | широко используется | разрешён | широко используется | разрешён | разрешён | — |
| ГОЭЛРО I очередь (1920)[5] | предпочтителен[р 4] | |||||
| ОСТ 569 (1928)[6] | предпочтителен | предпочтителен | разрешён | — | предпочтителен[р 5] | — |
| ОСТ 5155 (1932) | разрешён | разрешён | разрешён[р 6][р 7] | — | разрешён | |
| ГОСТ 721-41[7][8] | разрешён | разрешён | допускается сохранение существующих установок | разрешён | предпочтителен[р 8] | — |
| ГОСТ 5651-51[9][р 9] | разрешён | разрешён | -[р 10] | разрешён[р 10] | разрешён | — |
| ГОСТ 721-62 | разрешён | разрешён | допускается сохранение существующих установок | разрешён | предпочтителен | — |
| ГОСТ 5651-64[10][р 9] | — | разрешён | — | разрешён | разрешён | — |
| ГОСТ 721-74 | разрешён | разрешён | допускается сохранение существующих установок | разрешён | предпочтителен | |
| ГОСТ 21128-75[11] | разрешён | разрешён | — | для ранее разработанного оборудования[р 11] | предпочтителен | — |
| ГОСТ 23366-78 | разрешён | разрешён | — | для ранее разработанного оборудования | предпочтителен | — |
| ГОСТ 21128-83 | разрешён | разрешён | — | для ранее разработанного оборудования | предпочтителен | разрешён |
| ГОСТ 5651-89[р 9] | — | разрешён | — | — | разрешён | — |
| ГОСТ 29322-92 (МЭК 38-83) | — | — | — | — | разрешён до 2003 года | предпочтителен |
| ГОСТ 29322-2014 (IEC 60038:2009) | — | — | — | — | в текст стандарта внесено примечание: «Однако … до сих пор продолжают применять.» | предпочтителен |
Гармонические колебания. Амплитуда, период и частота колебательного движения
Урок 24. Физика 9 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Гармонические колебания. Амплитуда, период и частота колебательного движения»
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
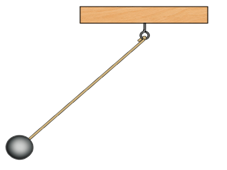
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.
Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
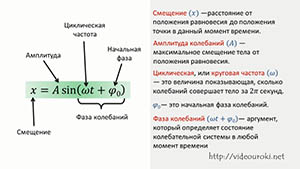
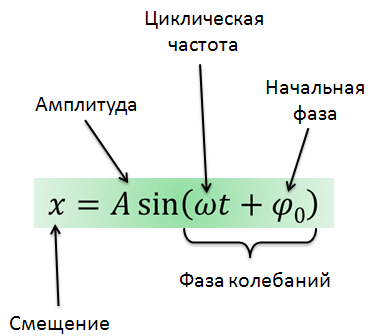
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
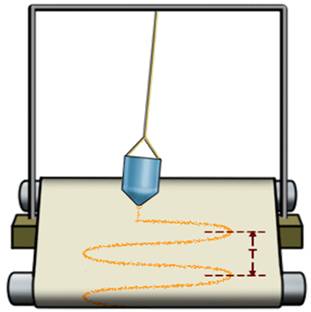
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда колебаний — максимальное смещение тела от положения равновесия.
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
– Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.