Что является примером временного ряда сейсмографический мониторинг
Временной ряд
Временной ряд — это упорядоченная последовательность значений какого-либо показателя за несколько периодов времени. Основная характеристика, которая отличает временной ряд от простой выборки данных, — указанное время измерения или номер изменения по порядку.
Пример временного ряда: биржевой курс.
Пример выборки данных: электронные почты клиентов магазина.
Где применяются временные ряды
Временные ряды используются для аналитики и прогнозирования, когда важно определить, что будет происходить с показателями в ближайший час/день/месяц/год: например, сколько пользователей скачают за день мобильное приложение. Показатели для составления временных рядов могут быть не только техническими, но и экономическими, социальными и даже природными.
Прогнозирование временных рядов
Модели ARMA и ARIMA
Они сыграли фундаментальную роль в обработке сигналов связи во время Второй мировой войны. После их начали использовать в анализе временных рядов в 1970 году.
ARMA (Autoregressive Moving Average) — авторегрессионная модель скользящей средней.
ARIMA (Autoregressive Integrated Moving Average) — авторегрессионная интегрированная модель скользящей средней.
AR → Авторегрессионная модель
В ней значения в будущем определяются как значения из прошлого, умноженные на коэффициенты.
Это относится к различным методам вычисления различий между последовательными наблюдениями для получения стационарного процесса из нестационарного.
MA → Модель скользящей средней
Это регрессионная модель, которая использует прошлые ошибки прогноза для прогнозирования интересующей переменной.
Для работы с временными рядами с сезонными компонентами используется SARIMA (интегрированное скользящее среднее сезонной авторегрессии). Это расширение модели ARIMA, добавляющее в нее сезонные условия.
Data Scientist с нуля
Получите востребованные IT-навыки за один год и станьте перспективным профессионалом. Мы поможем в трудоустройстве. Дополнительная скидка 5% по промокоду BLOG.
Prophet
Prophet разработан командой Facebook Core Data Science и представляет собой инструмент с открытым исходным кодом для бизнес-прогнозирования. Модель Prophet основана на трех переменных:
g (t) — тренд. Логистическая функция позволяет моделировать рост с насыщением, когда при увеличении показателя снижается темп его роста.
s (t) — сезонность отвечает за моделирование периодических изменений, связанных с недельной и годовой сезонностью.
h (t) — праздники и события. Учитываются аномальные дни, которые не влияют на сезонность.
ε(t) — ошибка. Содержит информацию, которую модель не учитывает.
У Prophet существует больше инструментов для обработки и сортировки данных по сезонности, чем у SARIMA. Такое преимущество позволяет анализировать временные ряды с различной сезонностью — неделей, месяцем, кварталом или годом.
Прогноз по методу экспоненциального сглаживания
Преимущество этого метода — возможность сделать прогноз на длительный период. Математически экспоненциальное сглаживание выражается так:
a (alfa) — коэффициент сглаживания, который принимает значения от 0 до 1. Он определяет, насколько продолжительность изменит существующие значения в базе данных.
x — текущее значение временного ряда (например, объем продаж).
y — сглаженная величина на текущий период.
t — значение тренда за предыдущий период.
Пример экспоненциального сглаживания:
Голубая линия на графике — это исходные данные, темно-синяя линия представляет экспоненциальное сглаживание временного ряда с коэффициентом сглаживания 0,3, а оранжевая линия использует коэффициент сглаживания 0,05. Чем меньше коэффициент сглаживания, тем более плавным будет временной ряд.
Временные ряды и их характеристики
Предполагается, что временные ряды генерируются регулярно, но на практике это не всегда так. В нерегулярных рядах измерения нельзя провести через одинаковые промежутки времени. Примером нерегулярного временного ряда является пополнение банковской карты.
Типы временных рядов
Помимо регулярности, временные ряды делятся на детерминированные и недетерминированные.
Детерминированный временной ряд — ряд, в котором нет случайных аспектов или показателей: он может быть выражен формулой. Это значит, что мы можем проанализировать, как показатели вели себя в прошлом, и точно прогнозировать их поведение в будущем.
Недетерминированный временной ряд имеет случайный аспект и прогнозирование будущих действий становится сложнее. Природа таких показателей случайна.
Стационарные и нестационарные ряды
На наблюдение за показателями и их систематизацией влияют тенденции и сезонные эффекты. От этих условий зависит сложность моделирования системы прогнозирования. Временные ряды можно разделить по наличию или отсутствию тенденций и сезонных эффектов на стационарные и нестационарные.
В стационарных временных рядах статистические свойства не зависят от времени, поэтому результат легко предсказать. Большинство статистических методов предполагают, что все временные ряды должны быть стационарными. Пример стационарных временных рядов — рождаемость в России. Конечно, она зависит от множества факторов, но ее спад или рост возможно предсказать: у рождаемости нет ярко выраженной сезонности.
В нестационарных временных рядах статистические свойства меняются со временем. Они показывают сезонные эффекты, тренды и другие структуры, которые зависят от временного показателя. Пример — международные перелеты авиакомпаний. Количество пассажиров на тех или иных направлениях меняется в зависимости от сезонности.
Для классических статистических методов удобнее создавать модели стационарных временных рядов. Если прослеживается четкая тенденция или сезонность во временных рядах, то следует смоделировать эти компоненты и удалить их из наблюдений.
Прогнозирование временных рядов — популярная аналитическая задача, которую используют в разных сферах жизни — бизнесе, науке, исследованиях общества и потребительского поведения. Прогнозы используются для предсказания, например, сколько серверов понадобится онлайн-магазину, когда спрос на товар вырастет.
Освойте необходимые навыки и инструменты и пройдите через все этапы работы над аналитическим проектом. Дополнительная скидка 5% по промокоду BLOG.
Временные ряды. Простые решения
В этой статье мы рассмотрим несколько простых подходов прогнозирования временных рядов.
Материал, изложенный в статье, на мой взгляд, хорошо дополняет первую неделю курса «Прикладные задачи анализа данных» от МФТИ и Яндекс. На обозначенном курсе можно получить теоретические знания, достаточные для решения задач прогнозирования рядов динамики, а в качестве практического закрепления материала предлагается с помощью модели ARIMA библиотеки scipy сформировать прогноз заработной платы в Российской Федерации на год вперед. В статье, мы также будем формировать прогноз заработной платы, но при этом будем использовать не библиотеку scipy, а библиотеку sklearn. Фишка в том, что в scipy уже предусмотрена модель ARIMA, а sklearn не располагает готовой моделью, поэтому нам придется потрудиться ручками. Таким образом, нам для решения задачи, в каком то смысле, необходимо будет разобраться как устроена модель изнутри. Также, в качестве дополнительного материала, в статье, задача прогнозирования решается с помощью однослойной нейронной сети библиотеки pytorch.
Весь код написан на python 3 в jupyter notebook. Более того, notebook устроен таким образом, что вместо данных о заработной плате можно подставить многие другие ряды динамики, например данные о ценах на сахар, поменять период прогнозирования, валидации и обучения, добавить иные внешние факторы и сформировать соответствующий прогноз. Другими словами, в работе используется простенький самописный тренажерчик, с помощью которого можно прогнозировать различные ряды динамики. Код можно посмотреть здесь
План статьи
Краткое описание тренажера
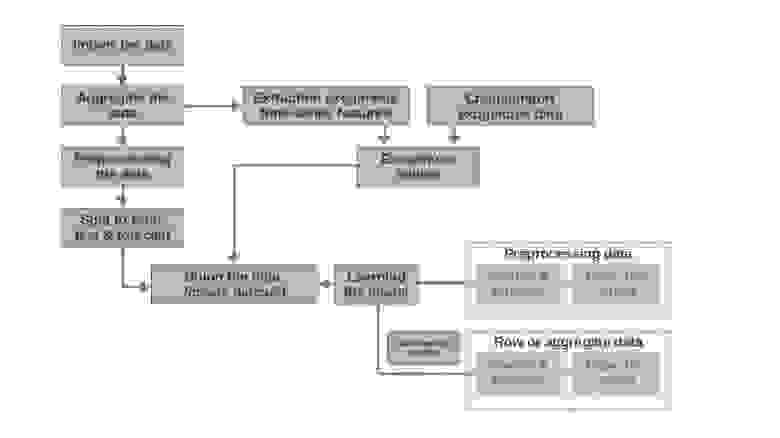
Import the data
Здесь все просто — импортируем данные. Иногда бывает так, что сырых данных достаточно для формирования более-менее внятного прогноза. Именно первый и второй прогнозы в статье моделируются на основании сырых данных, то есть для прогноза заработной платы используются необработанные данные о заработной плате в прошлые периоды.
Aggregate the data
В статье не используется агрегация данных ввиду отсутствия необходимости. Однако зачастую, данные могут быть представлены неравными временными интервалами. В таком случае, просто необходимо их агрегировать. Например, данные с торгов ценными бумагами, валютой и другими финансовыми инструментами необходимо агрегировать. Обычно берут среднее значение в интервале, но можно и максимальное, минимальное, стандартное отклонение и другие статистики.
Preprocessing the data
В нашем случае, речь идет в первую очередь о предобработке данных, благодаря которой, временной ряд приобретает свойство гомоскедастичности (через логарифмирование данных) и становится стационарным (через дифференцирование ряда).
Split to train, test & forecast
В этом блоке кода временные ряды разбиваются на периоды обучения, тестирования и прогнозирования путем добавления нового столбца с соответствующими значениями «train», «test», «forecast». То есть, мы не создаем три отдельных таблицы для каждого периода, а просто добавляем столбец, на основании, которого в дальнейшем будем разделять данные.
Extraction exogenous time-series features
Бывает полезным выделить дополнительные внешние (экзогенные) признаки из временного ряда. Например, указать выходной это день или нет, указать количество дней в месяце (или количество рабочих дней в месяце) и др. Как правило эти признаки «вытаскиваются» из самого временного ряда без какого либо ручного вмешательства.
Create/import exogenous data
Не всю информацию можно «вытащить» из временного ряда. Иногда могут потребоваться дополнительные внешние данные. Например, какие-то эпизодические события, которые оказывают сильное влияние на значения временного ряда. Такими событиями могут быть даты начала военных действий, введения санкций, природные катаклизмы и др. В работе такие факторы не рассматриваются, однако возможность их использования стоит иметь в виду.
Exogenous values
В этом блоке кода мы объединяем все экзогенные данные в одну таблицу.
Union the data (create dataset)
В этом блоке кода мы объединяем значения временного ряда и экзогенных признаков в одну таблицу. Другими словами — готовим датасет, на основании, которого будем обучать модель, тестировать качество и формировать прогноз.
Learning the model
Здесь все понятно — мы просто обучаем модель.
Preprocessing data: predict & forecast
В случае, если мы для обучения модели использовали предобаботанные данные (логарифмированные, обработанные функцией бокса-кокса, стационарный ряд и др.), то качество модели для начала оценивается на предобработанных данных и только потом уже на «сырых» данных. Если, мы данные не предобрабатывали, то данный этап пропускается.
Row data: predict & forecast
Данный этап является заключительным. Если, модель обучалась на предобработанных данных, например, мы их прологарифмировали, то для получения прогноза заработной платы в рублях, а не логарифма рублей, нам следует перевести прогноз обратно в рубли.
Также хотелось бы отметить, что в статье используется одномерный временной ряд для предсказания заработной платы. Однако ничего не мешает использовать многомерный ряд, например добавить данные курса рубля к доллару или какой-либо другой ряд.
Решение в лоб
Будем считать, что данные о заработной плате в прошлом, могут аппроксимировать заработную плату в будущем. Иначе можно сказать — размер заработной платы, например, в январе зависит от того, какая заработная плата была в декабре, ноябре, октябре,…
Давайте возьмем значения заработной платы в 12-ть прошлых месяцев для предсказания заработной платы в 13-й месяц. Другими словами для каждого целевого значения у нас будет 12 признаков.
Признаки будем подавать на вход Ridge Regression библиотеки sklearn. Параметры модели берем по умолчанию за исключением параметра alpha, его установили на 0, то есть по сути мы используем обычную регрессию.
Это и есть решение в лоб — оно самое простое:) Бывают ситуации, когда нужно очень срочно дать хоть какой-то результат, а времени на какую-либо предобработку просто нет или не хватает опыта, чтобы оперативно обработать или добавить данные. Вот в таких ситуациях, можно в качестве baseline использовать сырые данные для построения прогноза. Забегая вперед, отмечу, что качество модели оказалось сопоставимо с качеством моделей, в которых используется предобработка данных.
Давайте посмотрим, что у нас получилось.
На первый взгляд результат выглядит хоть и неидеально, но близко к действительности.
В соответствии со значениями коэффициентов регрессии, наибольшее влияние на прогноз заработной платы оказывает значение заработной платы ровно год назад.
Попробуем добавить в модель экзогенные переменные.
Добавление экзогенных переменных
Мы будем использовать 2 внешних признака: количество дней в месяце и номер месяца (от 1 до 12). Признак «Номер месяца» мы бинаризируем, в итоге у нас получится 12 столбцов для каждого месяца со значениями 0 или 1.
Сформируем новый датасет и посмотрим на качество модели.
Качество получилось ниже. Визуально заметно, что прогноз выглядит не совсем правдоподобно в части роста заработной платы в декабре.
Давайте теперь проведем первую предобработку данных.
Коррекция гетероскедастичности.
Если мы посмотрим на график заработной платы за период с 2010 по 2020 гг, то мы увидим, что ежегодно разброс заработной платы внутри года между месяцами растет.
Ежегодный рост дисперсии от месяца к месяцу приводит к гетероскедастичности. Для улучшения качества прогнозирования нам следует избавиться от этого свойства данных и привести их к гомоскедастичности.
Для этого воспользуемся обычным логарифмированием и посмотрим как выглядит прологарифмированный ряд.
Обучим модель на прологарифмированном ряду
В итоге качество предсказаний на обучающей и тестовой выборках действительно улучшилось, однако прогноз на 2021 год по сравнению с прогнозом первой модели визуально выглядит менее правдоподобным. Скорее всего использование экзогенных факторов ухудшает модель.
Приведение ряда к стационарному
Приводить ряд к стационарному будем следующим образом:
Ряд действительно выглядит стационарным, об этом также говорит значение критерия Дики-Фуллера.
Ожидать хорошее качество предсказаний на обучающей и тестовой выборках на обработанных данных, то есть на стационарном ряду не приходится, так как по сути, в этом случае модель должна предсказывать значения белого шума. Но нам, для прогнозирования заработной платы, уже совсем не обязательно использовать регрессию, так как, приводя ряд к стационарному, мы по-простому говоря, определили формулу аппроксимации целевой переменной. Но мы не будем отходить от канонов и воспользуемся регрессионной моделью, к тому же у нас есть экзогенные факторы.
Давайте посмотрим, что получилось.
Вот так выглядит предсказание стационарного ряда. Как и ожидали — не очень-то и хорошо 🙂
А вот предсказание и прогноз заработной платы.
Качество заметно улучшилось и прогноз визуально стал выглядеть правдоподобным.
Теперь сформируем прогноз без использования экзогенных переменных
Качество еще улучшилось и правдоподобность прогноза сохранилась 🙂
Прогнозирование с помощью однослойной нейронной сети
На вход нейронной сети будем подавать имеющиеся датасеты. Так как наша сеть однослойная, то по сути это и есть та же самая линейная регрессия с незамысловатыми модификациями и ожидать сильно большую разницу в качестве предсказаний не стоит.
Для начала посмотрим на саму сеть
Теперь пару слов о том, как будем ее обучать.
Не будем рассматривать качество предсказаний для каждого датасета отдельно (желающие могут посмотреть подробности на гите). Давайте сравним итоговые результаты.
Качество на тестовой выборке с использованием Ridge Regression
Качество на тестовой выборке с использованием Single layer NN
Как мы и ожидали, принципиальной разницы между обычной регрессией и простой однослойной нейронной сетью не оказалось. Конечно, нейронки дают больше маневра для обучения: можно менять оптимизаторы, регулировать шаги обучения, использовать скрытые слои и функции активации, можно пойти еще дальше и использовать рекуррентные нейронные сети — RNN. К слову, лично мне не удалось получить вменяемого качества в данной задаче с использованием RNN, однако на просторах интернета можно встретить много интересных примеров прогнозирования временных рядов с использованием LSTM.
На этом моменте статья подошла к завершению. Надеюсь, материал будет полезен как некий обзор baseline-подходов, применяемых при прогнозировании временных рядов и послужит хорошим практическим дополнением к курсу «Прикладные задачи анализа данных» от МФТИ и Яндекс.
Открытый курс машинного обучения. Тема 9. Анализ временных рядов с помощью Python
Доброго дня! Мы продолжаем наш цикл статей открытого курса по машинному обучению и сегодня поговорим о временных рядах.

UPD: теперь курс — на английском языке под брендом mlcourse.ai со статьями на Medium, а материалами — на Kaggle (Dataset) и на GitHub.
Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).
Введение
На работе я практически ежедневно сталкиваюсь с теми или иными задачами, связанными с временными рядам. Чаще всего возникает вопрос — а что у нас будет происходить с нашими показателями в ближайший день/неделю/месяц/пр. — сколько игроков установят приложения, сколько будет онлайна, как много действий совершат пользователи, и так далее. К задаче прогнозирования можно подходить по-разному, в зависимости от того, какого качества должен быть прогноз, на какой период мы хотим его строить, и, конечно, как долго нужно подбирать и настраивать параметры модели для его получения.
Начнем с простых методов анализа и прогнозирования — скользящих средних, сглаживаний и их вариаций.
Движемся, сглаживаем и оцениваем
Небольшое определение временного ряда:
Временной ряд – это последовательность значений, описывающих протекающий во времени процесс, измеренных в последовательные моменты времени, обычно через равные промежутки
Таким образом, данные оказываются упорядочены относительно неслучайных моментов времени, и, значит, в отличие от случайных выборок, могут содержать в себе дополнительную информацию, которую мы постараемся извлечь.
Импортируем нужные библиотеки. В основном нам понадобится модуль statsmodels, в котором реализованы многочисленные методы статистического моделирования, в том числе для временных рядов. Для поклонников R, пересевших на питон, он может показаться очень родным, так как поддерживает написание формулировок моделей в стиле ‘Wage
В качестве примера для работы возьмем реальные данные по часовому онлайну игроков в одной из мобильных игрушек:
Rolling window estimations
Начнем моделирование с наивного предположения — «завтра будет, как вчера», но вместо модели вида будем считать, что будущее значение переменной зависит от среднего
её предыдущих значений, а значит, воспользуемся скользящей средней.
Реализуем эту же функцию в питоне и посмотрим на прогноз, построенный по последнему наблюдаемому дню (24 часа)
Для нашего ряда тренды и так вполне очевидны, но если сгладить по дням, становится лучше видна динамика онлайна по будням и выходным (выходные — время поиграть), а недельное сглаживание хорошо отражает общие изменения, связанные с резким ростом числа активных игроков в феврале и последующим снижением в марте.

Модификацией простой скользящей средней является взвешенная средняя, внутри которой наблюдениям придаются различные веса, в сумме дающие единицу, при этом обычно последним наблюдениям присваивается больший вес.
Экспоненциальное сглаживание, модель Хольта-Винтерса
Простое экспоненциальное сглаживание
А теперь посмотрим, что произойдёт, если вместо взвешивания последних значений ряда мы начнем взвешивать все доступные наблюдения, при этом экспоненциально уменьшая веса по мере углубления в исторические данные. В этом нам поможет формула простого экспоненциального сглаживания:
Здесь модельное значение представляет собой средневзвешенную между текущим истинным и предыдущим модельным значениями. Вес называется сглаживающим фактором. Он определяет, как быстро мы будем «забывать» последнее доступное истинное наблюдение. Чем меньше
, тем больше влияния оказывают предыдущие модельные значения, и тем сильнее сглаживается ряд.
Экспоненциальность скрывается в рекурсивности функции — каждый раз мы умножаем на предыдущее модельное значение, которое, в свою очередь, также содержало в себе
, и так до самого начала.
Двойное экспоненциальное сглаживание
До сих пор мы могли получить от наших методов в лучшем случае прогноз лишь на одну точку вперёд (и ещё красиво сгладить ряд), это здорово, но недостаточно, поэтому переходим к расширению экспоненциального сглаживания, которое позволит строить прогноз сразу на две точки вперед (и тоже красиво сглаживать ряд).
В этом нам поможет разбиение ряда на две составляющие — уровень (level, intercept) и тренд
(trend, slope). Уровень, или ожидаемое значение ряда, мы предсказывали при помощи предыдущих методов, а теперь такое же экспоненциальное сглаживание применим к тренду, наивно или не очень полагая, что будущее направление изменения ряда зависит от взвешенных предыдущих изменений.
В результате получаем набор функций. Первая описывает уровень — он, как и прежде, зависит от текущего значения ряда, а второе слагаемое теперь разбивается на предыдущее значение уровня и тренда. Вторая отвечает за тренд — он зависит от изменения уровня на текущем шаге, и от предыдущего значения тренда. Здесь в роли веса в экспоненциальном сглаживании выступает коэффициент . Наконец, итоговое предсказание представляет собой сумму модельных значений уровня и тренда.
Теперь настраивать пришлось уже два параметра — и
. Первый отвечает за сглаживание ряда вокруг тренда, второй — за сглаживание самого тренда. Чем выше значения, тем больший вес будет отдаваться последним наблюдениям и тем менее сглаженным окажется модельный ряд. Комбинации параметров могут выдавать достаточно причудливые результаты, особенно если задавать их руками. А о не ручном подборе параметров расскажу чуть ниже, сразу после тройного экспоненциального сглаживания.
Тройное экспоненциальное сглаживание a.k.a. Holt-Winters
Итак, успешно добрались до следующего варианта экспоненциального сглаживания, на сей раз тройного.
Идея этого метода заключается в добавлении еще одной, третьей, компоненты — сезонности. Соответственно, метод применим только в случае, если ряд этой сезонностью не обделён, что в нашем случае верно. Сезонная компонента в модели будет объяснять повторяющиеся колебания вокруг уровня и тренда, а характеризоваться она будет длиной сезона — периодом, после которого начинаются повторения колебаний. Для каждого наблюдения в сезоне формируется своя компонента, например, если длина сезона составляет 7 (например, недельная сезонность), то получим 7 сезонных компонент, по штуке на каждый из дней недели.
Получаем новую систему:
Уровень теперь зависит от текущего значения ряда за вычетом соответствующей сезонной компоненты, тренд остаётся без изменений, а сезонная компонента зависит от текущего значения ряда за вычетом уровня и от предыдущего значения компоненты. При этом компоненты сглаживаются через все доступные сезоны, например, если это компонента, отвечающая за понедельник, то и усредняться она будет только с другими понедельниками. Подробнее про работу усреднений и оценку начальных значений тренда и сезонных компонент можно почитать здесь. Теперь, имея сезонную компоненту, мы можем предсказывать уже не на один, и даже не на два, а на произвольные шагов вперёд, что не может не радовать.
Ниже приведен код для построения модели тройного экспоненциального сглаживания, также известного по фамилиям её создателей — Чарльза Хольта и его студента Питера Винтерса.
Дополнительно в модель включен метод Брутлага для построения доверительных интервалов:
где — длина сезона,
— предсказанное отклонение, а остальные параметры берутся из тройного сглаживани. Подробнее о методе и о его применении к поиску аномалий во временных рядах можно прочесть здесь
Кросс-валидация на временных рядах, подбор параметров
Перед тем, как построить модель, поговорим, наконец, о не ручной оценке параметров для моделей.
Ничего необычного здесь нет, по-прежнему сначала необходимо выбрать подходящуюю для данной задачи функцию потерь: RMSE, MAE, MAPE и др., которая будет следить за качеством подгонки модели под исходные данные. Затем будем оценивать на кросс-валидации значение функции потерь при данных параметрах модели, искать градиент, менять в соответствии с ним параметры и бодро опускаться в сторону глобального минимума ошибки.
Небольшая загвоздка возникает только в кросс-валидации. Проблема состоит в том, что временной ряд имеет, как ни парадоксально, временную структуру, и случайно перемешивать в фолдах значения всего ряда без сохранения этой структуры нельзя, иначе в процессе потеряются все взаимосвязи наблюдений друг с другом. Поэтому придется использовать чуть более хитрый способ для оптимизации параметров, официального названия которому я так и не нашел, но на сайте CrossValidated, где можно найти ответы на всё, кроме главного вопроса Жизни, Вселенной и Всего Остального, предлагают название «cross-validation on a rolling basis», что не дословно можно перевести как кросс-валидация на скользящем окне.
Суть достаточно проста — начинаем обучать модель на небольшом отрезке временного ряда, от начала до некоторого , делаем прогноз на
шагов вперед и считаем ошибку. Далее расширяем обучающую выборку до
значения и прогнозируем с
до
, так продолжаем двигать тестовый отрезок ряда до тех пор, пока не упрёмся в последнее доступное наблюдение. В итоге получим столько фолдов, сколько
уместится в промежуток между изначальным обучающим отрезком и всей длиной ряда.
Значение длины сезона 24*7 возникло не случайно — в исходном ряде отчетливо видна дневная сезонность, (отсюда 24), и недельная — по будням ниже, на выходных — выше, (отсюда 7), суммарно сезонных компонент получится 24*7.
В модели Хольта-Винтерса, как и в остальных моделях экспоненциального сглаживания, есть ограничение на величину сглаживающих параметров — каждый из них может принимать значения от 0 до 1, поэтому для минимизации функции потерь нужно выбирать алгоритм, поддерживающий ограничения на параметры, в данном случае — Truncated Newton conjugate gradient.
Передадим полученные оптимальные значения коэффициентов ,
и
и построим прогноз на 5 дней вперёд (128 часов)
Судя по графику, модель неплохо описала исходный временной ряд, уловив недельную и дневную сезонность, и даже смогла поймать аномальные снижения, вышедшие за пределы доверительных интервалов. Если посмотреть на смоделированное отклонение, хорошо видно, что модель достаточно резко регирует на значительные изменения в структуре ряда, но при этом быстро возвращает дисперсию к обычным значениям, «забывая» прошлое. Такая особенность позволяет неплохо и без значительных затрат на подготовку-обучение модели настроить систему по детектированию аномалий даже в достаточно шумных рядах.
Эконометрический подход
Стационарность, единичные корни
Перед тем, как перейти к моделированию, стоит сказать о таком важном свойстве временного ряда, как стационарность.
Под стационарностью понимают свойство процесса не менять своих статистических характеристик с течением времени, а именно постоянство матожидания, постоянство дисперсии (она же гомоскедастичность) и независимость ковариационной функции от времени (должна зависеть только от расстояния между наблюдениями). Наглядно можно посмотреть на эти свойства на картинках, взятых из поста Sean Abu:
Почему стационарность так важна? По стационарному ряду просто строить прогноз, так как мы полагаем, что его будущие статистические характеристики не будут отличаться от наблюдаемых текущих. Большинство моделей временных рядов так или иначе моделируют и предсказывают эти характеристики (например, матожидание или дисперсию), поэтому в случае нестационарности исходного ряда предсказания окажутся неверными. К сожалению, большинство временных рядов, с которыми приходится сталкиваться за пределыми учебных материалов, стационарными не являются, но с этим можно (и нужно) бороться.
Чтобы бороться с нестационарностью, нужно узнать её в лицо, потому посмотрим, как её детектировать. Для этого обратимся к белому шуму и случайному блужданию, чтобы выяснить как попасть из одного в другое бесплатно и без смс.
График белого шума:
Итак, процесс, порожденный стандартным нормальным распределением, стационарен, колеблется вокруг нуля с отклонением в 1. Теперь на основании него сгенерируем новый процесс, в котором каждое последующее значение будет зависеть от предыдущего:



На первом графике получился точно такой же стационарный белый шум, который строился раньше. На втором значение увеличилось до 0.6, в результате чего на графике стали появляться более широкие циклы, но в целом стационарным он быть пока не перестал. Третий график всё сильнее отклоняется от нулевого среднего значения, но всё ещё колеблется вокруг него. Наконец, значение
равное единице дало процесс случайного блуждания — ряд не стационарен.
Происходит это из-за того, что при достижении критической единицы, ряд перестаёт возвращаться к своему среднему значению. Если вычесть из левой и правой части
, то получим
, где выражение слева — первые разности. Если
, то первые разности дадут стационарный белый шум
. Этот факт лёг в основу теста Дики-Фуллера на стационарность ряда (наличие единичного корня). Если из нестационарного ряда первыми разностями удаётся получить стационарный, то он называется интегрированным первого порядка. Нулевая гипотеза теста — ряд не стационарен, отвергалась на первых трех графиках, и принялась на последнем. Стоит сказать, что не всегда для получения стационарного ряда хватает первых разностей, так как процесс может быть интегрированным с более высоким порядком (иметь несколько единичных корней), для проверки таких случаев используют расширенный тест Дики-Фуллера, проверяющий сразу несколько лагов.
Бороться с нестационарностью можно множеством способов — разностями различного порядка, выделением тренда и сезонности, сглаживаниями и преобразованиями, например, Бокса-Кокса или логарифмированием.
Избавляемся от нестационарности и строим SARIMA
Попробуем теперь построить ARIMA модель для онлайна игроков, пройдя все круги ада стадии приведения ряда к стационарному виду. Про саму модель уже не раз писали на хабре — Построение модели SARIMA с помощью Python+R, Анализ временных рядов с помощью python, поэтому подробно останавливаться на ней не буду.
Как и следовало ожидать, исходный ряд стационарным не является, критерий Дики-Фуллера не отверг нулевую гипотезу о наличии единичного корня. Попробуем стабилизировать дисперсию преоразованием Бокса-Кокса.
Уже лучше, однако критерий Дики-Фуллера по-прежнему не отвергает гипотезу о нестационарности ряда. А автокорреляционная функция явно намекает на сезонность в получившемся ряде. Возьмём сезонные разности:
Критерий Дики-Фуллера теперь отвергает нулевую гипотезу о нестационарности, но автокорреляционная функция всё ещё выглядит нехорошо из-за большого числа значимых лагов. Так как на графике частной автокорреляционной функции значим лишь один лаг, стоит взять еще первые разности, чтобы привести наконец ряд к стационарному виду.
Наконец, получили стационарный ряд, по автокорреляционной и частной автокорреляционной функции прикинем параметры для SARIMA модели, на забыв, что предварительно уже сделали первые и сезонные разности.
Начальные приближения Q = 1, P = 4, q = 3, p = 4
Лучшие параметры загоняем в модель:
Проверим остатки модели:
Что ж, остатки стационарны, явных автокорреляций нет, построим прогноз по получившейся модели
В финале получаем достаточно адекватный прогноз, в среднем модель ошибалась на 1.3 K пользователей, что очень и очень неплохо, однако суммарные затраты на подготовку данных, приведение к стационарности, определение и перебор параметров могут такой точности и не стоить.
Линейные и не очень модели на временных рядах
Снова небольшое лирическое отступление. Часто на работе приходится строить модели, руководствуясь одним основополагающим принципом – быстро, качественно, недорого. Поэтому часть моделей могут банально не подойти для «продакшн-решений», так как либо требуют слишком больших затрат по подготовке данных (например, SARIMA), либо сложно настраиваются (хороший пример – SARIMA), либо требуют частого переобучения на новых данных (опять SARIMA), поэтому зачастую гораздо проще бывает выделить несколько признаков из имеющегося временного ряда и построить по ним обычную линейную регрессию или навесить решаюший лес. Дешево и сердито.
Возможно, этот подход не является значительно подкрепленным теорией, нарушает различные предпосылки, например, условия Гаусса-Маркова, особенно пункт про некоррелированность ошибок, однако на практике нередко выручает и достаточно активно используется в соревнованиях по машинному обучению.
Извлечение признаков (Feature extraction)
Помимо стандартных признаков вроде лагов целевой переменной, много информации содержат в себе дата и время. Про извлечение признаков из них уже здорово описано в одной из предыдущих статей курса.
| y | hour | weekday | is_weekend | |
|---|---|---|---|---|
| Time | ||||
| 2017-01-01 00:00:00 | 34002 | 0 | 6 | 1 |
| 2017-01-01 01:00:00 | 37947 | 1 | 6 | 1 |
| 2017-01-01 02:00:00 | 41517 | 2 | 6 | 1 |
| 2017-01-01 03:00:00 | 44476 | 3 | 6 | 1 |
| 2017-01-01 04:00:00 | 46234 | 4 | 6 | 1 |
Посмотрим на средние по дням недели
Помимо перечисленных преобразований для увеличения числа признаков используют и множество других метрик, например, максимальное/минимальное значение, наблюдавшееся в скользящем по ряду окне, медианы, число пиков, взвешенные дисперсии и многое другое. Автоматически этим занимается уже упоминавшаяся в курсе библиотека библиотека tsfresh.
Для удобства все преобразования можно записать в одну функцию, которая сразу же будет возвращать разбитые на трейн и тест датасеты и целевые переменные.
Линейная регрессия vs XGBoost
Обучим на получившихся данных простую линейную регрессию. При этом лаги будем брать начиная с двенадцатого, таким образом модель будет способна строить предсказания на 12 часов вперёд, имея фактические наблюдения за предыдущие пол дня.
Получилось достаточно неплохо, даже отбора признаков модель ошибается, в среднем, на 3K пользователей в час, и это учитывая огромный выброс в середине тестового ряда.
Также можно провести оценку модели на кросс-валидации, тому же принципу, что был использован ранее. Для этого воспользуемся функцией (с небольшими модификациями), предложенной в посте Pythonic Cross Validation on Time Series
На 5 фолдах получили среднюю абсолютную ошибку в 4.6 K пользователей, достаточно близко к оценке качества, полученной на тестовом датасете.
Почему бы теперь не попробовать XGBoost.

Те же 3 K пользователей в средней абсолютной ошибке, и неплохо пойманные аномалии на тестовом датасете. Конечно, чтобы уменьшить ошибку, еще можно повозиться с параметрами, настроить при необходимости регуляризацию, отобрать признаки, понять, на сколько лагов нужно уходить вглубь истории и т.д.
Заключение
Мы познакомились с разными методами и подходами к анализу и прогнозированию временных рядов. К сожалению, или к счастью, серебряной пули для решения такого рода задач пока не появилось. Методы, разработанные в 60-е годы прошлого века, (а некоторые и в начале 19-го), по-прежнему пользуются популярностью наравне с неразобранными в рамках данной статьи LSTM или RNN. Отчасти это связано с тем, что задача прогнозирования, как и любая другая задача, возникающая в процессе работы с данными — во многом творческая и уж точно исследовательская. Несмотря на обилие формальных метрик качества и способов оценки параметров, для каждого временного ряда часто приходится подбирать и пробовать что-то своё. Не последнюю роль играет и баланс между качеством и трудозатратами. Не раз уже упоминавшаяся здесь SARIMA-модель хотя и демонстрирует выдающиеся результаты при должной настройке, может потребовать не одного часа танцев с бубном манипуляций с рядом, в то время как простенькую линейную регрессию можно соорудить за 10 минут, получив при этом более-менее сравнимые результаты.
Домашнее задание
Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.
В демо-версии домашнего задания вы будете предсказывать просмотры wiki-страницы «Machine Learning». Веб-форма для ответов, там же найдете и решение.
Полезные ресурсы
Материал статьи доступен в GitHub-репозитории курса
в виде тетрадок Jupyter.









