Что является сегментом интегрирования
Тест по теме «Интегралы»
ТЕСТ по теме «Интегралы»
На каждый вопрос нужно выбрать один верный ответ.
1.Что называется интегрированием:
1. операция нахождения интеграла;
2. преобразование выражения с интегралами;
3. операция нахождения производной;
4. предел приращения функции к приращению её аргумента
2.Что является сегментом интегрирования?
1. круговая область, где интеграл существует;
2. промежуток, на котором необходимо проинтегрировать функцию;
3. корни существования подынтегральной функции;
4. подынтегральная функция
1.метод сведения к табличным интегралам;
2.метод определения интеграла, т.е. переход к пределу интегральных сумм;
3.метод геометрических преобразований;
4.С помощью, какой формулы, в основном, решаются задания по нахождению определенного интеграла:
3. используя формулы преобразования интеграла
5.Чему равен неопределенный интеграл от 0?
6. Когда применяется метод интегрирования неопределенных интегралов по частям?
1. когда функция имеет квадратный корень;
2. не применяется данный метод нигде;
3. когда подынтегральное выражение содержит множители функций ln(x); arccos(x); arcsin (x);
4. функция гиперболическая.
7. С помощью какой универсальной подстановкой рационализируется тригонометрическая функция:
8. Чему равен неопределенный интеграл от 1?
10. Для чего используют метод замены переменной (метод подстановки) интеграла?
1. свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой переменной;
2. просто необходимо выполнить какие-нибудь преобразования;
3. для усложнения подынтегральной функции;
4. для того, чтобы потом можно было бы использовать метод Римана.
Что является сегментом интегрирования?
1. круговая область, где интеграл существует;
2. промежуток, на котором необходимо проинтегрировать функцию;
3. корни существования подынтегральной функции;
4. подынтегральная функция
1.метод сведения к табличным интегралам;
2.метод определения интеграла, т.е. переход к пределу интегральных сумм;
3.метод геометрических преобразований;
4.С помощью, какой формулы, в основном, решаются задания по нахождению определенного интеграла:
3. используя формулы преобразования интеграла
Чему равен неопределенный интеграл от 0?
Вариант 2
Когда применяется метод интегрирования неопределенных интегралов по частям?
1. когда функция имеет квадратный корень;
2. не применяется данный метод нигде;
3. когда подынтегральное выражение содержит множители функций ln(x); arccos(x); arcsin (x);
4. функция гиперболическая.
2. С помощью какой универсальной подстановкой рационализируется тригонометрическая функция:
Чему равен неопределенный интеграл от 1?
Для чего используют метод замены переменной (метод подстановки) интеграла?
1. свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой переменной;
2. просто необходимо выполнить какие-нибудь преобразования;
3. для усложнения подынтегральной функции;
4. для того, чтобы потом можно было бы использовать метод Римана.
Таблица правильных ответов
| Задания | 1 | 2 | 3 | 4 | 5 |
| 1 вариант | 1 | 2 | 2 | 4 | 4 |
| 2 вариант | 3 | 1 | 1 | 1 | 1 |
Тема 10: «Координаты и векторы»
Вариант 1
1. Треугольник АВС – проекция треугольника MNP на плоскость α, точка D лежит на отрезке АВ, причем точки А,В, С и D – проекции точек М, N, P и К соответственно. Найдите МN, если АD-4см, DВ=6см, МК=6см.
б) 15см г) другой ответ
2. Плоскость α, параллельная стороне АВ треугольника АВС, пересекает его в точках А1 и В1, лежащих на прямых АС и ВС соответственно. Найдите А1С, если: АС=15см, А1В1=4см, АВ=20см.
б) 4см г) другой ответ
3. Найдите расстояние от некоторой точки до плоскости квадрата, если расстояние от этой точки до всех его сторон равно 4 см, а сторона квадрата равна 2 см.
а) 

б) 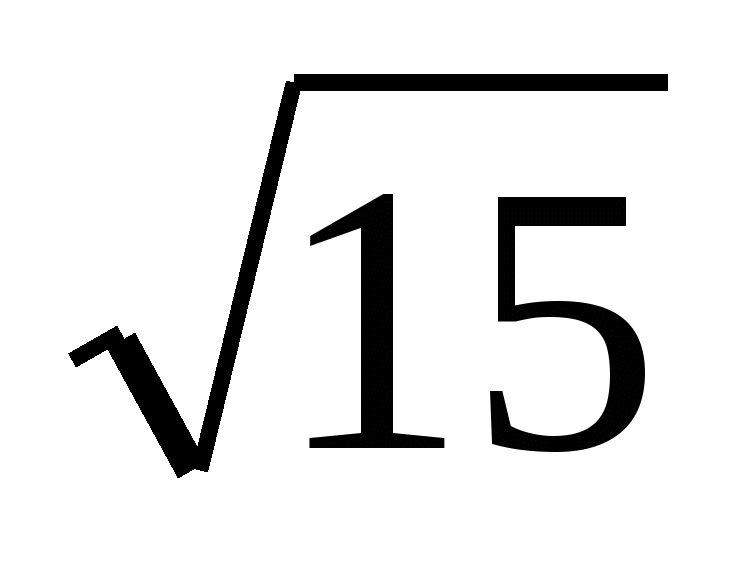
б) 32 см г) другой ответ
5. При каком значении а длина вектора АВ равна 3 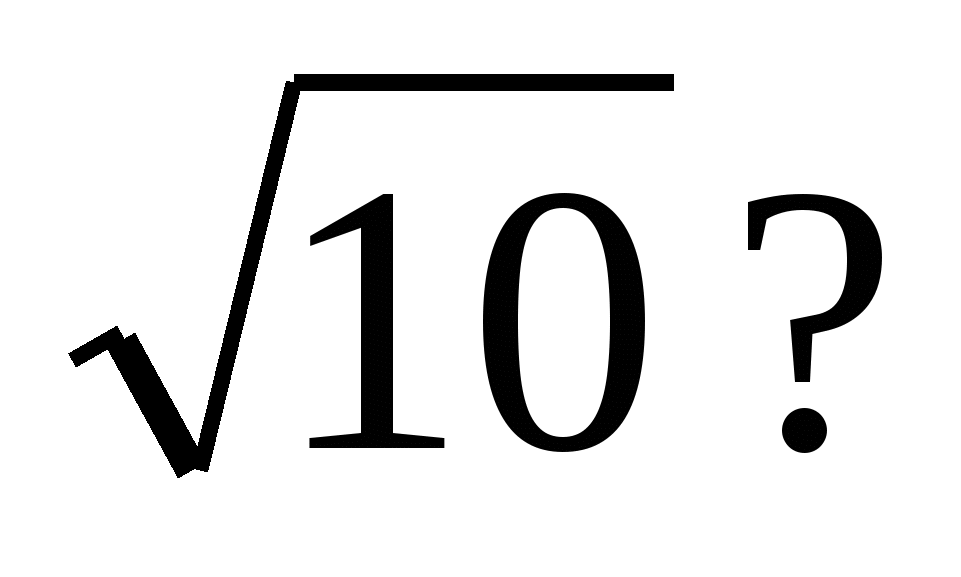
6. Точка С – проекция точки С1 на плоскость α. Найдите косинус угла между плоскостью треугольника АВС1 и α, где АВ принадлежит α, если треугольник АВС1- равносторонний, а угол АСВ- прямой.
а) 
б) 
7. Точка В делит отрезок АС в отношении 2:3. Найдите координаты точки В, если А(1;-2;4), с(6;12;9).
Вариант 2
1. Треугольник FСA– проекция треугольника LTS на плоскость α, точка B лежит на отрезке FC, причем точки F, С,A и B – проекции точек L,T,S и D соответственно. Найдите LD, если FB=7см, BC=3см, DT=12см.
б) 21см г) другой ответ
2. Плоскость α, параллельная стороне АВ треугольника АВС, пересекает его в точках А1 и В1, лежащих на прямых АС и ВС соответственно. Найдите А1А, если: А1С=5см, А1 В1=7см, АВ=21см.
б) 15см г) другой ответ
3. Расстояние от некоторой точки до плоскости квадрата равно 3см. Найдите расстояние от этой точки до его вершин, если оно одинаковое для всех вершин, а сторона квадрата равна 4см
а) 
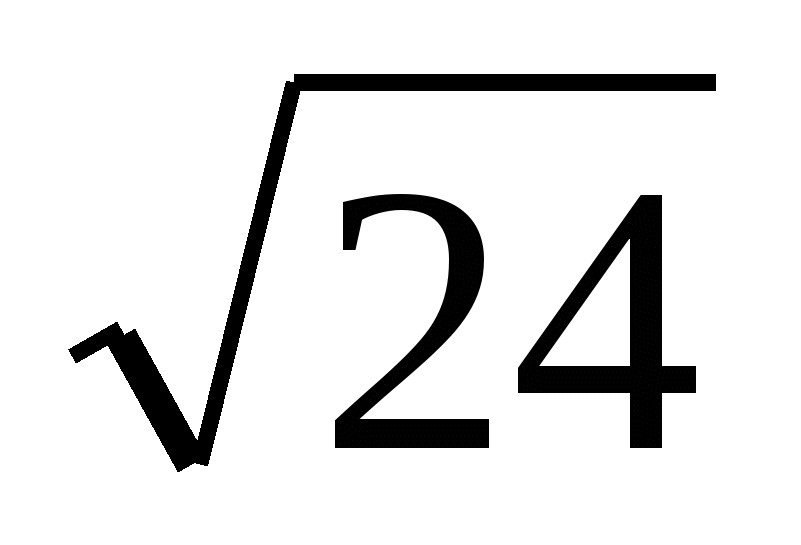
б) 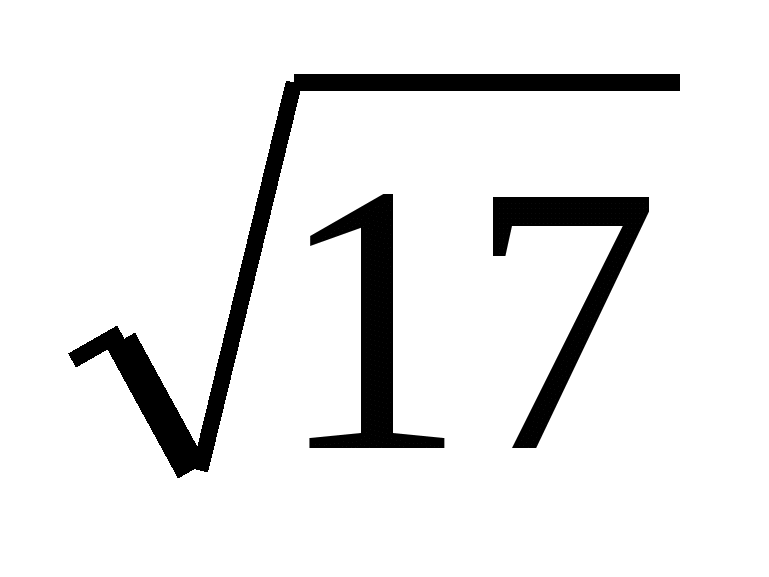
б) 23 см г) другой ответ
5. При каком значении а длина вектора АВ равна 2 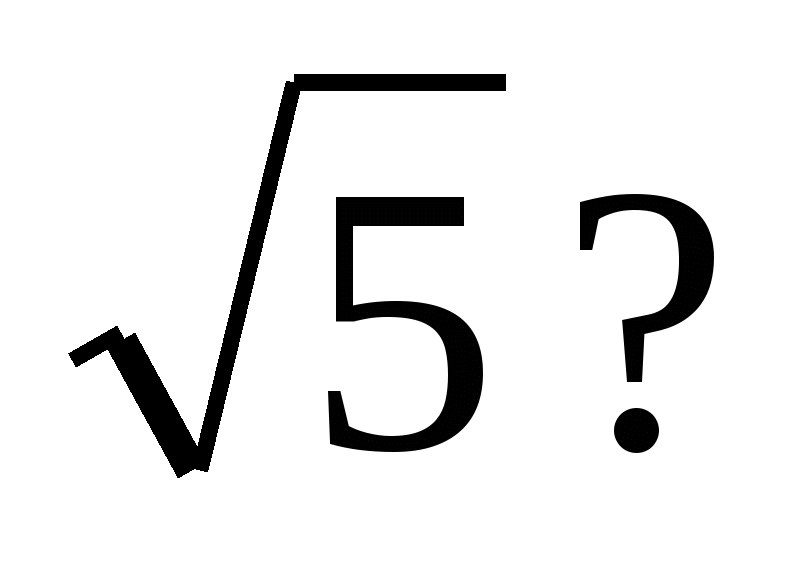
6. Найдите косинус угла между плоскостями, в которых лежат равнобедренные треугольники СDВ и СDА, где СD-общее основание, если СD=2см; СВ=2см; СА= 4см
б) 
7. Точка В делит отрезок АС в отношении 4:1. Найдите координаты точки В, если А(-1;32), С(4;13;12).
Тест на тему Интегралы
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
ТЕСТ по теме «Интегралы»
На каждый вопрос нужно выбрать один верный ответ.
1.Что называется интегрированием:
1. операция нахождения интеграла;
2. преобразование выражения с интегралами;
3. операция нахождения производной;
4. предел приращения функции к приращению её аргумента
2.Что является сегментом интегрирования?
1. круговая область, где интеграл существует;
2. промежуток, на котором необходимо проинтегрировать функцию;
3. корни существования подынтегральной функции;
4. подынтегральная функция
1.метод сведения к табличным интегралам;
2.метод определения интеграла, т.е. переход к пределу интегральных сумм;
3.метод геометрических преобразований;
4.С помощью, какой формулы, в основном, решаются задания по нахождению определенного интеграла:
3. используя формулы преобразования интеграла
5.Чему равен неопределенный интеграл от 0?
6. Когда применяется метод интегрирования неопределенных интегралов по частям?
1. когда функция имеет квадратный корень;
2. не применяется данный метод нигде;
3. когда подынтегральное выражение содержит множители функций ln(x); arccos(x); arcsin (x);
4. функция гиперболическая.
7. С помощью какой универсальной подстановкой рационализируется тригонометрическая функция:
8. Чему равен неопределенный интеграл от 1?
10. Для чего используют метод замены переменной (метод подстановки) интеграла?
1. свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой переменной;
2. просто необходимо выполнить какие-нибудь преобразования;
3. для усложнения подынтегральной функции;
4. для того, чтобы потом можно было бы использовать метод Римана.
Количество правильных ответов (%)
Количество правильных ответов
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1183654
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В Москве новогодние каникулы в школах могут начаться с 27 декабря
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
ВПР для школьников в 2022 году пройдут весной
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Экспресс-подготовка к онлайн-тестированию:
для студентов дистанционного обучения, при устройстве на работу, прохождении аттестаций
Сдаешь тесты самостоятельно?
Закажи скайп-консультацию и узнай все секреты успешной сдачи экзаменов онлайн!
Математика Тесты с ответами Тема 7-12
Для быстрого поиска по странице нажмите Ctrl+F и в появившемся окошке напечатайте слово запроса (или первые буквы)
Тема 7. Интегральное исчисление (часть 1)
Отметьте верные утверждения
совокупность всех производных функции называется неопределенным интегралом от этой функции
+неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого
+если в определение интеграла ʃ f(x)dx = F(x) + С вместо аргумента х подставить выражение (kх + b), то это приведет к появлению дополнительного множителя 1/k перед первообразной
+производная от первообразной для некоторой функции равна самой этой функции
функция F(x) = 2х является первообразной для функции f(x) = х2.
Производная функции имеет вид …
одна первообразная функции
совокупность всех производных функции
совокупность всех дифференциалов функции
площадь криволинейной трапеции, ограниченной графиком функции, осью абсцисс и еще двумя прямыми
+совокупность всех первообразных функции
Отметьте верные утверждения:
+a) ʃ dF(x)=F(x)+C, C – const
b) d( ʃ f(x)dx) = ʃ f(x)dx
d) ʃ dF(x)=C*F(x), C – const
Производная произведения (x+2)e x равна …
г) e x-1 ( e +2 x + x 2 )
Тема 8. Интегральное исчисление (часть 2)
Отметьте верные утверждения:
+a) функция F(x)=x 3 /3+6,5 является первообразной для f(x)=x 2
+b) совокупность все первообразны функций называется неопределенным интегралом от этой функции
c) функция F(x)= x 2 является первообразной для f(x)= x 3 /3
d) – правильная дробь
+e) – рациональная дробь
Множество первообразны функции f(x)=1/(2-2x) имеет вид …
К методам интегрирования относятся:
+интегрирование по частям
+метод нелинейной подстановки
+ метод линейной подстановки
Отметьте верные утверждения:
+c) интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций
e) дробь НЕ является рациональной
Функция F(х) называется первообразной функцией для функции f(x) на промежутке X, если…
хотя бы в одной точке х этого промежутка F ‘(x) = f(x)
+если в каждой точке х этого промежутка F ‘(x) = f(x)
хотя бы в одной точке х этого промежутка f ‘(x) = F(x)
если в каждой точке х этого промежутка f ‘(x) = F(x)
Тема 9. Интегральное исчисление (часть 3)
Определенный интеграл – это (отметьте верные утверждения)…
для неположительной функции площадь криволинейной трапеции, ограниченной графиком этой функции, прямыми х = а, х = b и осью абсцисс
предел производной функции при стремлении аргумента к нулю
разложение неопределенного интеграла на множители
+для неположительной функции площадь криволинейной трапеции, ограниченной графиком этой функции, прямыми х = а, х = b и осью абсцисс, взятая со знаком минус
+предел интегральной суммы при стремлении наибольшей из длин отрезков к нулю
Интегральная сумма – это…
предел суммы произведений длин отрезков, на которые разбит отрезок интегрирования на значения функции в точках этих отрезков
+сумма произведений длин отрезков, на которые разбит отрезок интегрирования, на значения функции в точках этих отрезков
Для рационализации интеграла можно использовать:
дифференцирование пределов интегрирования
+выражение синуса и косинуса через тангенс половинного аргумента с последующей заменой переменной
замену неопределенного интеграла на определенный
Отметьте верные утверждения:
все свойства определенного интеграла аналогичны свойствам неопределенного интеграла
+производная от интеграла с переменным верхним пределом по верхнему пределу равна подынтегральной функции
+постоянный множитель можно выносить за знак определенного интеграла
Отметьте верные утверждения:
+3) интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций
5) дробь НЕ является рациональной
Определитель равен …
Определитель равен …
Тема 11. Основные свойства определителей
Для матрицы не существует обратной, если x равно …
При перестановке местами двух столбцов матрицы ее определитель
становится равным нулю
Если матрица содержит одинаковые строки, то ее определитель равен …
Если строка матрицы состоит из одних нулей, то определитель матрицы равен
Для матрицы не существует обратной, если значение x равно …
Тема 12. Ранг матрицы
Что такое ранг матрицы?
порядок обратной матрицы
+наивысший порядок отличных от нуля миноров этой матрицы
отличный от нуля определитель матрицы
Какие преобразования матрицы относятся к элементарным?
+умножение всех элементов строки или столбца матрицы на число, отличное от нуля
прибавление к каждому элементу строки или столбца одного и того же числа
вычитание другой матрицы
+изменение порядка строк (столбцов) матрицы.
Если система линейных уравнений имеет более одного решения, то такая система.
У какой из этих матриц ранг может равняться четырем?
квадратная матрица третьего порядка
+матрица размерности четыре на пять
матрица размерности три на четыре
Если система линейных уравнений имеет только одно решение, то такая система.
Что является сегментом интегрирования
Автор: Козырева Татьяна Александровна
Организация: ГАПОУ КК КИТТ
Населенный пункт: г. Краснодар
План — конспект открытого урока по дисциплине «Математика: алгебра и начала математического анализа, геометрия»
Группа:
Преподавателя математики ГАПОУ КК КИТТ, учителя высшей категории Козыревой Т.А.
Специальность:
09.01.01 Наладчик аппаратного и программного обеспечения
Тема:
Применение определенного интеграла для нахождения площади криволинейной трапеции.
Тип урока:
Вид урока:
Цели:
Методы и приемы
работы:
методы контроля знаний:
устные (опрос, взаимопроверка, рецензия ответа);
письменные (составление плана, тест);
игровые (соревнование, игра на внимание);
графический (графический диктант);
комбинированные (самоконтроль, рефлексивная карта, рейтинг)
Материально-техническое обеспечение урока
Используемые
технологии:
План урока:
Приветствие :
Здравствуйте! (СЛАЙД 1)
Я отправляю всем Вам пожелания Успеха!
Сегодня у нас необычный урок. Урок- телемост! Общение с отсутствующими на данном уроке будет через интернет.
Сегодня у нас открытый урок и присутствуют гости. Поприветствуем их (поклон джентльменов )
Поприветствуем участников телемоста. Те, кто присутствуют через Яндекс- телемост машут рукой.
Цитата: Математика! Как я люблю тебя,
В течение очень многих лет.
Таинственней, величавей, строже
Чем ты, на свете предметов нет!
Организационный момент (2-3 мин.):
Это 4-я. Новаторы 21 века
3-я Умники 21 века. Капитаны команд,пожалуйста, встаньте.
Графический диктант
На каждый вопрос отвечаете «ДА» или «НЕТ»
1.Что называется интегрированием:
1. операция нахождения интеграла;«ДА»
2.Что является сегментом интегрирования?
1. круговая область, где интеграл существует; «НЕТ»
промежуток, на котором необходимо проинтегрировать функцию;
1.метод сведения к табличным интегралам; «НЕТ»
2.метод определения интеграла, т.е. переход к пределу интегральных сумм;
4.С помощью, какой формулы, в основном, решаются задания по нахождению определенного интеграла:
4. формулы Ньютона — Лейбница. «ДА»
5.Чему равен неопределенный интеграл от 0?
const C.
6. Когда применяется метод интегрирования неопределенных интегралов по частям?
когда подынтегральное выражение содержит множители функций ln(x); arccos(x); arcsin (x);
1. функция гиперболическая.«НЕТ»
7. Чему равен неопределенный интеграл от 1?
9.Для чего используют метод замены переменной (метод подстановки) интеграла?
1. свести исходный интеграл к более простому с помощью перехода от старой переменной интегрирования к новой переменной; «ДА»
(Слайд 6,презентация 2)
Взаимопроверка: 1 ряд передает тетради 2 ряду, 2р.-3-му, 3р.- 1-му.
Подсчет правильных ответов, т.е задание выполнено без ошибок- количество балов команде. ТЕЛЕМОСТ- участвует. Проверяют работу друг у друга, демонстрируя проверку.
Каждой парте условие на отдельном листке. раздает капитан- вытаскивают пример не глядя. Начинает 1 парта, решая любой из предложенных примеров. Лист ответов заполняет каждая парта. На проверку передают другому ряду капитаны. Проверка- 1 мин.(по СЛАЙДУ 8)
Математика на протяжении всей истории человеческой культуры всегда была её неотъемлемой частью; она является ключом к познанию окружающего мира, базой научно-технического прогресса и важным компонентом развития личности. На уроке мы рассматривали применение интеграла в физике и убедись в том, что математика нам помогает познать окружающий нас мир, изучать физические законы природы.
Изучение нового материала. Тема нашего урока «Площадь криволинейной трапеции».
Вы знакомы с понятием «определенный интеграл» и научились его вычислять.
Сегодня мы сформулируем понятие «криволинейная трапеция» и научимся вычислять ее площадь с помощью определенного интеграла. Метод контрольных вопросов: Как ВЫ думаете, какими будут наши ЦЕЛИ: Научиться вычислять площадь криволинейной трапеции.
Изучить “метод исчерпывания ” Архимеда.
Сформировать понятие объема фигур.
Ознакомить с понятиями “Философия Пифагора”.
Формирование у студентов прочных знаний, умений и навыков по нахождению площади криволинейной трапеции.
Формирование умений проводить исследования по заданной теме.
Развивать навыки самоконтроля и взаимоконтроля.
Развивать умения сравнивать, анализировать.
Расширять границы самопознания.
Развитие познавательного интереса, логического мышления.
ЗАДАЧИ: уточнить
Задаем вопрос: Умеем ли мы решать такие примеры?
Знаем ли мы способы решения? Используем методику 5 вопросов! Выслушиваем предложения.
1.Вспомним какие темы мы с вами изучили на последних уроках. Интегралы.
2. Что еще раннее изученное будем использовать? Построение графиков. Решение уравнений ( когда будем находить границы интегрирования).
3.Сможем ли мы применить эти умения в решении этой задачи.
4.Как нам помогут графики. Ясно видна площадь фигуры, площадь которой мы находим!
5. Какие формулы для вычисления будем использовать для вычисления площади?
Спасибо ВСЕМ за хорошую работу на уроке!




