Чтобы найти неизвестное делимое что надо сделать
Как найти делимое
Как найти неизвестное делимое? Поможет правило:
А что делать, если правило вдруг забылось?
В этом случае нужно придумать несложный пример на деление, с его помощью понять, что делать для нахождения делимого, и применить этот вывод, чтобы найти неизвестное делимое в своем уравнении.
Например: 10:5=2. Здесь делимое — 10. Чтобы найти 10, надо 2 умножить на 5. Точно так же поступаем при решении своего примера.
Теперь посмотрим, как найти делимое, на конкретных примерах.
| x | : | 12 | = | 60 |
| дл | дт | ч |
Чтобы найти неизвестное делимое, нужно частное умножить на делитель:
| k | : | 7 | = | 11 |
| дл | дт | ч |
Для нахождения делимого частное умножаем на делитель:
Более сложные примеры, где помимо деления есть и другие действия, мы рассмотрим позже.
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Чтобы научиться быстро и успешно решать уравнения, нужно начать с самых простых правил и примеров. В первую очередь надо научиться решать уравнения, слева у которых стоит разность, сумма, частное или произведение некоторых чисел с одним неизвестным, а справа другое число. Иными словами, в этих уравнениях есть одно неизвестное слагаемое и либо уменьшаемое с вычитаемым, либо делимое с делителем и т.д. Именно об уравнениях такого типа мы с вами поговорим.
Эта статья посвящена основным правилам, позволяющим найти множители, неизвестные слагаемые и др. Все теоретические положения будем сразу пояснять на конкретных примерах.
Нахождение неизвестного слагаемого
Для нахождения неизвестного слагаемого надо вычесть известное из суммы.
Зная это правило, мы можем найти одно неизвестное слагаемое, используя известное и сумму. Какое именно слагаемое мы знаем, первое или второе, в данном случае неважно. Посмотрим, как применить данное правило на практике.
Обычно решения подобных уравнений записывают следующим образом:
Такая форма записи нужна для того, чтобы проиллюстрировать последовательную замену исходного уравнения равносильными и отобразить процесс нахождения корня. Решение нашего простого уравнения, приведенного выше, правильно будет записать так:
Нахождение неизвестного вычитаемого или уменьшаемого
Как мы уже упоминали в первом пункте, между процессами сложения и вычитания существует определенная связь. С ее помощью можно сформулировать правило, которое поможет найти неизвестное уменьшаемое, когда мы знаем разность и вычитаемое, или же неизвестное вычитаемое через уменьшаемое или разность. Запишем эти два правила по очереди и покажем, как применять их при решении задач.
Для нахождения неизвестного уменьшаемого надо прибавить вычитаемое к разности.
Переходим к следующему правилу.
Для нахождения неизвестного вычитаемого надо вычесть разность из уменьшаемого.
Перед тем, как перейти к другим правилам, отметим, что существует правило переноса любых слагаемых из одной части уравнения в другую с заменой знака на противоположный. Все приведенные выше правила ему полностью соответствуют.
Нахождение неизвестного множителя
Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.
Нахождение неизвестного делимого или делителя
Еще один случай, который нам нужно рассмотреть, – это нахождение неизвестного делимого, если мы знаем делитель и частное, а также нахождение делителя при известном частном и делимом. Сформулировать это правило мы можем с помощью уже упомянутой здесь связи между умножением и делением.
Для нахождения неизвестного делимого нужно умножить делитель на частное.
Посмотрим, как применяется данное правило.
Вот краткая запись всего решения:
Указанное правило можно интерпретировать как умножение правой и левой части уравнения на одинаковое отличное от 0 число. Это преобразование никак не влияет на корни уравнения.
Переходим к следующему правилу.
Для нахождения неизвестного делителя нужно разделить делимое на частное.
Последовательное применение правил
Зачастую на практике встречаются более сложные задачи, в которых правила нахождения слагаемых, уменьшаемых, вычитаемых, множителей, делимых и частных нужно применять последовательно. Приведем пример.
Вот краткая запись решения еще одного уравнения ( 2 · x − 7 ) : 3 − 5 = 2 :
Нахождение неизвестных множителя, делимого или делителя
Урок 23. Математика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Нахождение неизвестных множителя, делимого или делителя»
Множитель, множитель, произведение. Делимое, делитель, частное.
Сегодня у нас непростой урок, ведь нам предстоит разобраться, как находить неизвестные: множитель, делимое или делитель. А для чего это надо уметь? Догадались? Ну конечно для того, чтобы уверенно решать уравнения! И мы, конечно же, решим несколько уравнений. Но прежде надо кое-что вспомнить.
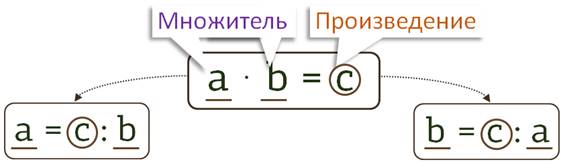
Я предлагаю вам посмотреть на буквенную запись действия умножения.
А и Б в этой записи являются множителями, Ц – произведением. Понятно, что произведение мы получаем действием умножения. Это – целое, то есть наибольшее число. А вот множители являются частями. Значит, их мы находим обратным действием, делением.
То есть, если нужно найти неизвестный множитель, мы произведение делим на известный множитель.
А теперь посмотрим на буквенную запись деления:
Обычно, целое можно разделить на части. Поэтому К, делимое, является целым, а М и Н – это части. И, естественно, что целое мы находим умножением. Поэтому, если надо найти неизвестное делимое, мы перемножаем делитель с частным.
А вот делитель является частью. И, если надо найти неизвестный делитель, то его мы найдём, разделив делимое на частное.
Ну а теперь пришло время решать уравнения. Давайте разберём вот это уравнение:
Посмотрите, это у нас осложнённое уравнение. Поэтому, прежде всего, надо его упростить, то есть, выполнить действие в правой части уравнения. Сто двадцать шесть разделить на два равно шестьдесят три. Переписываем уравнение, заменив действие деления на его результат. Здесь надо найти неизвестный множитель. Чтобы найти неизвестный множитель, мы произведение делим на известный множитель.
Шестьдесят три делим на девять, получается семь.
Не забываем выполнить проверку уравнения. Сначала переписываем его, заменив икс на его значение, которое мы получили – семь. Семью девять – шестьдесят три. Сто двадцать шесть разделить на два – шестьдесят три. Левая и правая части уравнения равны, значит, уравнение решено верно. Решаем следующее уравнение:
Неизвестное делимое находим умножением.
Ну, а следующее уравнение я предлагаю вам решить самостоятельно.
Какой компонент здесь надо найти? Неизвестный делитель. А его мы находим
Проверьте, ребята, так ли решено у вас уравнение?
Видите, как помогает при решении уравнений знание правил.
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Чтобы найти неизвестное делимое, надо делитель умножить на частное.
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
Выучите их, ребята, и не забывайте пользоваться при решении уравнений. Пока! До новых встреч!