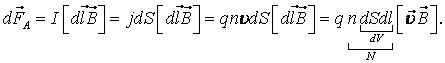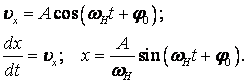движение альфа частицы в магнитном поле

Лекция 19

1.Сила Лоренца.

Это выражение для силы, которая действует на Nчастиц. Тогда на одну частицу действует сила, равная

Данное выражение называется магнитной составляющей силы Лоренца. Если учесть, что кроме материального поля может существовать и электрическое, то полное выражение для силы Лоренца имеет вид

2.Движение заряженной частицы в однородном магнитном поле

Данное уравнение является весьма сложным, т.к. и в общем случае зависят от пространственных и временной координат. Кроме того, сама частица также создает собственное электромагнитное поле.

Пусть электрического поля нет вообще, а магнитное имеет одну составляющую и однородно.

Вдоль поля скорость не меняется, движение равномерное.

Таким образом, поперечная скорость не меняется. Следовательно, не меняется модуль скорости вообще. Следовательно, не меняется кинетическая энергия частиц, а значит, магнитное поле не совершает работы над частицами. Это и понятно, т.к. магнитная составляющая силы Лоренца всегда перпендикулярна скорости, и эта сила не совершает работу. Такие силы называются гироскопическими. Если работа не совершается, то изменение магнитного потока равно нулю, а т.к. поле однородно, то не изменяется площадь фигуры, которую охватывает траектория движения частицы.

Аналогично можно поступить и для второй координаты и получить уравнение вида

Таким образом, траекторией частицы в плоскости XOY является окружность и частица движется по этой окружности с циклической частотой

,

которая называется Ларморовской или циклотронной частотой.

Частота и период не зависят от скорости частиц, т.е. от её кинетической энергии.

Радиус этой окружности равен

Вдоль поля частица перемещается равномерно. Следовательно, траектория частицы – винтовая линия с шагом

3.Масс-спектрометрия.

Очевидно, что удельный заряд частицы связан с радиусом её траектории в магнитном поле.

Это один из способов разделения изотопов.

4.Эффект Холла

Пусть жестко закрепленный проводник с током помещен в магнитное поле.

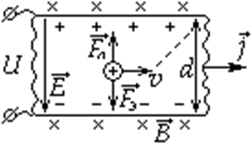
R – постоянная Холла.

Определив экспериментально постоянную Холла, можно узнать концентрацию частиц. Так была установлена концентрация электронов в металлах.

5.Магнитогидродинамический генератор.

В настоящее время МГД-генераторы пока еще не нашли широкого промышленного применения.

Источник

11 класс

§ 19. Движение заряженных частиц в магнитном поле. Сила Лоренца

Сила Лоренца.

Значительный интерес представляет движение заряженных частиц в области пространства, где одновременно имеются электрическое и магнитное поля. Для этого случая Лоренц получил выражение для силы, которую в честь него называют силой Лоренца. Она представляет собой сумму сил, действующих на заряженную частицу, которая движется в электрическом и магнитном полях.

Её модуль можно найти с помощью закона Ампера. Предположим, что проводник с током находится в однородном магнитном поле. Вдоль проводника движутся заряженные частицы. Рассмотрим отрезок проводника длиной Δl и площадью поперечного сечения S (рис. 3.38).

На него со стороны магнитного поля действует сила Ампера. В § 1 «Условия существования электрического тока. Электрический ток в проводниках» была выведена формула, определяющая силу тока в проводнике:

Подставив это выражение в формулу для модуля силы Ампера F_A = BIΔlsin α, получим

где N = nSΔl — число заряженных частиц в рассматриваемом объёме SΔl. Магнитная составляющая силы Лоренца равна по модулю

Магнитная составляющая силы Лоренца всегда перпендикулярна плоскости, в которой располагаются вектор скорости заряженной частицы и вектор индукции магнитного поля.

В силу того что данная сила перпендикулярна скорости частицы, она не совершает работы.

Для определения направления магнитной составляющей силы Лоренца используют правило левой руки.

Если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца показывали направление скорости движения положительно заряженной частицы, то отогнутый (в плоскости ладони) на 90° большой палец покажет направление действующей на заряженную частицу магнитной составляющей силы Лоренца.

Если в магнитном поле движутся отрицательно заряженные частицы, то пальцы левой руки следует располагать противоположно направлению вектора скорости. Для иллюстрации применения правила левой руки приведём рисунок 3.39.

На нём штриховыми линиями указаны траектории движения зарядов (на рис. 3.39, а — положительного заряда, на рис. 3.39, б — отрицательного заряда).

Движение заряженной частицы в однородном магнитном поле.

Рассмотрим наиболее простой случай движения заряженной частицы в магнитном поле — это движение в однородном магнитном поле с индукцией, перпендикулярной начальной скорости частицы (рис. 3.40).

Так как магнитное поле не изменяет модуля скорости заряженной частицы, то остаётся неизменным и модуль магнитной составляющей силы Лоренца. Поскольку эта сила перпендикулярна скорости, то частица движется с центростремительным ускорением. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что радиус кривизны R траектории частицы постоянен. Частица движется равномерно по окружности радиусом R. Согласно второму закону Ньютона,

Следовательно, измерив R при известных υ и В, мы можем определить удельный заряд различных частиц.

Масс-спектрограф.

1 Масс-спектрограф был впервые сконструирован в 1919 г. учеником Дж. Дж. Томсона — Франсисом Астоном (1877—1945). C помощью этого прибора он произвёл точные измерения масс и дефектов масс ряда изотопов.

На рисунке 3.41, а изображена схема простейшего масс-спектрографа, а на рисунке 3.41, б — внешний вид современного прибора. Вакуумная камера масс-спектрографа помещена в магнитное поле (вектор магнитной индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с большой точностью измерить радиус траектории R. По этому радиусу можно определить удельный заряд иона и, следовательно, его массу.

Циклотрон.

Используя формулу для радиуса траектории, найдём время прохождения заряженной частицей полуокружности:

т. е. Δt зависит только от свойств частицы и индукции магнитного поля.

Этот факт был использован американским физиком Эрнестом Лоуренсом (1901 — 1958), который в 1931 г. создал циклотрон. Это устройство позволяет ускорять заряженные частицы сравнительно небольшим электрическим полем в течение ряда циклов. Рассмотрим устройство циклотрона (рис. 3.42).

Два электрода специальной формы — дуанты находятся в камере, где поддерживается вакуум (рис. 3.43).

Дуанты помещают между полюсами сильного магнита, и к ним подводится переменная разность потенциалов. В центре камеры между дуантами располагают источник заряженных частиц. В тот момент, когда между дуантами существует высокая разность потенциалов, электрическое поле в промежутке между ними ускоряет заряженные частицы.

Ускоренные частицы влетают во внутреннюю часть дуанта, где электрическое поле практически отсутствует. Двигаясь под действием магнитной составляющей силы Лоренца по окружности, заряженные частицы через половину оборота снова появляются в щели между дуантами.

Те из частиц, которые двигались с подходящей скоростью, пройдут через щель как раз в тот момент (через половину периода изменения приложенного к дуантам напряжения), когда там электрическое поле успеет сменить своё направление на противоположное. Такие частицы снова ускоряются, описывают внутри другого дуанта полуокружность ещё большего радиуса и снова в необходимый момент подходят к ускоряющему промежутку (время прохождения частицами полуокружности остаётся неизменным, так как оно не зависит от скорости частицы) и т. д. Остальные частицы ускоряются незначительно или совсем не ускоряются.

Циклотроны и другие более мощные ускорители заряженных частиц (например, фазотроны, синхротроны, синхрофазотроны) находят широкое применение в ядерной физике и физике элементарных частиц. Изучая столкновения ускоренных частиц с частицами мишени, физики получают возможность исследовать строение микрочастиц, действующие между ними силы, взаимные превращения элементарных частиц.

Магнитный щит земли.

Магнитное поле Земли оказывает существенное влияние на поток заряженных частиц из космоса (космические лучи). Оно образует третий «защитный пояс» наряду с атмосферой и ионосферой, защищающий живые организмы на Земле от губительного действия космических лучей.

На большой высоте магнитное поле Земли невелико, но захватывает громадные области пространства. Действуя на заряженную частицу длительное время, оно существенно изменяет её траекторию. Вместо прямой линии получается спираль, навивающаяся на линии индукции магнитного поля (рис. 3.44).

На летящую вдоль линии магнитной индукции частицу сила Лоренца не действует. Вот почему частицы свободно могут приближаться к полюсам, откуда веером расходятся линии магнитной индукции.

Кроме того, магнитное поле Земли удерживает на большой высоте заряженные частицы не слишком больших энергий. Эти области с повышенной концентрацией заряженных частиц, окружающих земной шар, называют радиационными поясами. Большинство частиц внешнего радиационного пояса Земли составляют электроны, а её внутреннего радиационного пояса — протоны (рис. 3.45).

Протоны задерживаются более сильным магнитным полем во внутреннем радиационном поясе. В радиационных поясах заряженные частицы движутся от одного полюса к другому, оставаясь в «магнитной ловушке».

Вопросы:

а) электрической составляющей силы Лоренца;

б) магнитной составляющей силы Лоренца?

2. В каком случае магнитная составляющая силы Лоренца будет максимальной?

3. Как можно определить направление магнитной составляющей силы Лоренца, действующей:

а) на положительно заряженную частицу;

б) на отрицательно заряженную частицу?

4. Для чего используют:

5. Как влияет магнитное поле Земли на потоки космических лучей?

Вопросы для обсуждения:

1. Действует ли магнитная составляющая силы Лоренца:

а) на незаряженную частицу в однородном магнитном поле;

б) на заряженную частицу, покоящуюся в магнитном поле;

в) на заряженную частицу, движущуюся вдоль линий магнитного поля?

Пример решения задачи

Модуль скорости электрона равен 10 6 м/с. В направлении осей X и Y магнитное поле безгранично. На каком расстоянии от точки влёта электрон вылетит из поля? Отношение заряда электрона к его массе e/m = 1,76 ∙ 10 11 Кл/кг.

В магнитном поле под действием магнитной составляющей силы Лоренца электрон опишет дугу окружности. Найдём её радиус R. Запишем второй закон Ньютона:

Ответ: l = 8 мм.

Упражнения:

1. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Чему равна скорость протона?

2. Найдите ускорение протона, который движется со скоростью 2 м/с в магнитном поле с индукцией 3 мТл перпендикулярно линиям магнитной индукции.

3. Определите кинетическую энергию электрона, движущегося по окружности радиусом 1 см в однородном магнитном поле с индукцией 0,03 Тл. Приведите ответ в Дж и в эВ.

4. Протон с энергией 600 эВ влетает в однородное магнитное поле с индукцией 0,33 Тл перпендикулярно линиям магнитной индукции. Найдите радиус траектории протона. Будет ли изменяться кинетическая энергия протона при движении в этом магнитном поле?

5. Электрон влетает в однородное магнитное поле с индукцией 9,4 мТл так, что вектор его скорости составляет угол 30° с направлением линий магнитной индукции (рис. 3.47).

Определите радиус витков траектории электрона и расстояние, пройденное им вдоль линии магнитной индукции за три витка. Скорость электрона равна 2,5 ∙ 10 6 м/с.

Источник

Julia и движение заряженной частицы в электромагнитном поле

Закрепляем навыки решения и визуализации дифференциальных уравнений на примере одного из самых распространенных эволюционных уравнений, вспоминаем о старом-добром Scilab и пытаемся понять, а надо ли оно нам… Под катом картинки (килобайт на семьсот)

и приступим к постановке задачи

Движение заряженных частиц в электромагнитном поле

На заряженую частицу с зарядом движущуюся в ЭМП со скоростью действует сила Лоренца: . Данная формула справедлива при ряде упрощений. Пренебрегая поправками на теорию относительности, считаем массу частицы постоянной, так что уравнение движения имеет вид:

Направим ось Y вдоль электрического поля, ось Z — вдоль магнитного поля и предположим для простоты, что начальная скорость частицы лежит в плоскости XY. В этом случае вся траектория частицы также будет лежать в этой плоскости. Уравнения движения примут вид:

Обезразмерим: . Звёздочками обозначены размерные величины, а — характерный размер рассматриваемой физической системы. Получим безразмерную систему уравнений движения заряженной частицы в магнитном поле:

В качестве начальной конфигурации модели выберем: Тл, В/м, м/с. Для численного решения воспользуемся пакетом DifferentialEquations:

Здесь используется метод Эйлера, для которого задаётся количество шагов. Также сохраняется в матрицу ответов не всё решение системы, а только 1 и 2 индексы, то есть координаты икс и игрек (скорости нам не нужны).

Проверим результат. Введем вместо х новую переменную . Таким образом осуществляется переход в новую систему координат, движущуюся относительно исходной со скоростью u в направлении оси Х:

Если выбрать и обозначить , то система упростится:

Электрическое поле исчезло из последних равенств, и они представляют собой уравнения движения частицы, находящейся под действием однородного магнитного поля. Таким образом, частица в новой системе координат (х, у) должна двигаться по окружности. Так как эта новая система координат сама перемещается относительно исходной со скоростью , то результирующее движение частицы будет складываться из равномерного движения по оси X и вращения по окружности в плоскости XY. Как известно, траектория, возникающая при сложении таких двух движений, в общем случае представляет собой трохоиду. В частности, если начальная скорость равна нулю, реализуется простейший случай движения такого рода — по циклоиде.
Удостоверимся, что скорость дрейфа вышла действительно равной Е/В. Для этого:

Out: 8.333333333333332e-5
С точностью до седьмого порядка!
Для удобства определим функцию, принимающую параметры модели и подпись графика, которая будет также служить названием файла png, создаваемого в папке с проектом (работает в Juno/Atom и Jupyter). В отличии от Gadfly, где графики создавались в слоях, а потом выводились функцией plot(), в Plots, чтобы в одном фрейме наделать разных графиков, первый из них создается функцией plot(), а последующие добавляются использованием plot!(). Названия функций меняющих принимаемые объекты в Джулии принято оканчивать восклицательным знаком.

При нулевой начальной скорости, как и предполагалось, получаем циклоиду:

Получим траекторию частицы при занулении индукции, напряженности и при смене знака заряда. Напомню, что точка значит поочередное выполнение функции со всеми элементами массива

Немного о Scilab

На Хабре уже есть достаточно информации о Сайлабе, например 1, 2, а тут про Octave поэтому ограничимся ссылками на Википедию и на домашнюю страницу.

От себя добавлю, про наличие удобного создания интерфейса с флажками кнопками и выводом графиков и довольно интересного инструмента визуального моделирования Xcos. Последний можно использовать, например, для моделирования сигнала в электротехнике:

И здесь очень удобное руководство:

Собственно, нашу задачу вполне можно решить и в Scilab:

Здесь информация по функции для решения дифуров ode. В принципе напрашивается вопрос

А зачем нам Julia?

… если и так есть такие замечательные штуки как Scilab, Octave и Numpy, Scipy?
Про последние два не скажу — не пробовал. Да и вообще вопрос сложный, так что прикинем навскидку:

Scilab
На харде займет чуть больше 500 Мб, запускается быстро и сходу доступно и дифуросчитание, и графика и всё остальное. Хорош для начинающих: отличное руководство (по большей части локализованное), есть много книг на русском. Про внутренние ошибки уже было сказано тут и здесь, и так как продукт очень нишевый, сообщество вялое, и дополнительные модули весьма скудны.

Julia
По мере добавления пакетов (особенно всякой питонщины а-ля Jupyter и Mathplotlib) разрастается от 376 Мб до вполне-таки шести с лишним гигабайт. Оперативку она тоже не щадит: на старте 132 Мб и после того, как в Юпитере намалевать графиков, до 1 ГБ спокойно дойдёт. Если работать в Juno, то всё почти как в Scilab: можно выполнять код сразу в интерпретаторе, можно печатать во встроенном блокноте и сохранять как файл, есть обозреватель переменных, журнал команд и интерактивная справка. Лично у меня вызывает возмущение отсутствие clear(), т. е. запустил я код, потом начал там поправлять и переименовывать, а старые переменные-то остались (в Юпитере нет обозревателя переменных).

Но всё это не критично. Scilab подходит вполне на первых парах, сделать лабу, курсач или посчитать чего промежуточного — очень даже подручный инструмент. Хоть здесь тоже есть поддержка параллельного вычисления и вызов сишных/фортрановских функций, для чего серьезного его использовать не получается. Большие массивы повергают его в ужас, чтоб задать многомерные, приходится заниматься всяким мракобесием, а вычисления за рамками классических задач вполне могут обронить всё вместе с операционкой.

И вот после всех этих болей и разочарований можно смело переходить на Julia, чтоб огрести ещё и здесь. Будем учиться дальше, благо комьюнити очень отзывчивое, проблемы утрясаются быстро, да и у Джулии есть еще много интересных особенностей, которые превратят процесс обучения в увлекательное путешествие!

Источник