движение электрона в магнитном поле по окружности
Шпаргалка по общей электронике и электротехнике.
5. ДВИЖЕНИЕ ЭЛЕКТРОНОВ В ОДНОРОДНОМ МАГНИТНОМ ПОЛЕ.
В некоторых электровакуумных приборах используется движение электронов в магнитном поле.
Рассмотрим случай, когда электрон влетает в однородное магнитное поле с начальной скоростью v0, направленной перпендикулярно магнитным силовым линиям. В этом случае на движущийся электрон действует так называемая сила Лоренца F, которая перпендикулярна вектору нО и вектору напряженности магнитного поля Н. Величина силы F определяется выражением: F= еv0Н.
При v0 = 0 сила Рравна нулю, т. е. на неподвижный электрон магнитное поле не действует.
Сила F искривляет траекторию электрона в дугу окружности. Поскольку сила F действует под прямым углом к скорости нО, она не совершает работы. Энергия электрона и его скорость не изменяются по величине. Происходит лишь изменение направления скорости. Известно, что движение тела по окружности (вращение) с постоянной скоростью получается благодаря действию направленной к центру центростремительной силы, которой именно и является сила F.
Направление поворота электрона в магнитном поле в соответствии с правилом левой руки удобно определяется по следующим правилам. Если смотреть в направлении магнитных силовых линий, то электрон движется по часовой стреле. Иначе говоря, поворот электрона совпадает с вращательным движением винта, который ввинчивается по направлению магнитных силовых линий.
Определим радиус r окружности, описываемой электроном. Для этого воспользуемся выражением для центростремительной силы, известным из механики: F = mv20/r. Приравняем его значению силы F = еv0Н: mv20/r = еv0Н. Теперь из этого уравнения можно найти радиус: r= mv0/(еН).
Чем больше скорость электрона v0, тем сильнее он стремится двигаться прямолинейно по инерции и радиус искривления траектории будет больше. С другой стороны, с увеличением Н растет сила F, искривление траектории возрастает и радиус окружности уменьшается.
Выведенная формула справедлива для движения в магнитном поле частиц с любыми массами и зарядом.
Рассмотрим зависимость rот mи е. Заряженная частица с большей массой mсильнее стремится лететь по инерции прямолинейно и искривление траектории уменьшится, т. е. rстанет больше. А чем больше заряд е, тем больше сила F и тем сильнее искривляется траектория, т. е. ее радиус становится меньше.
Выйдя за пределы магнитного поля, электрон дальше летит по инерции по прямой линии. Если же радиус траектории мал, то электрон может описывать в магнитном поле замкнутые окружности.
Таким образом, магнитное поле изменяет только направление скорости электронов, но не ее величину, т. е. между электроном и магнитным полем нет энергетического взаимодействия. По сравнению с электрическим полем действие магнитного поля на электроны является более ограниченным. Именно поэтому магнитное поле применяется для воздействия на электроны значительно реже, нежели электрическое поле.
Движение электронов в однородном магнитном поле
Рассмотрим движение электрона в однородном магнитном поле. Если неоднородность поля незначительна, или если нет необходимости в получении точных количественных оценок, то для изучения движения в неоднородном поле также можно пользоваться более простыми законами, полученными для однородного поля.
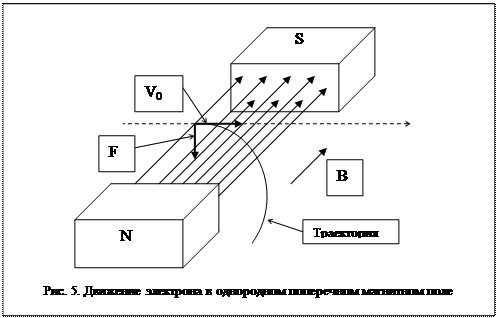
Пусть электрон влетает в однородное магнитное поле с начальной скоростью V0, направленной перпендикулярно магнитным силовым линиям, рис. 5. В этом случае на электрон действует сила Лоренца F, которая перпендикулярна вектору V0 и вектору магнитной индукции В, а численно равна:
.
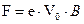
При V0=0 сила F также равна нулю (на неподвижный электрон магнитное поле не действует). Сила F искривляет траекторию электрона в дугу окружности. Так как сила F действует под прямым углом к скорости V0, она не совершает работы. Энергия электрона и его скорость не изменяются. Изменяется лишь направление движения.
Направление движения электрона определяется следующему мнемоническому правилу: поворот электрона совпадает с вращательным движением винта, который ввинчивается в направлении магнитных силовых линий. Это правило часто называют правилом буравчика.
Известно, что движение тела по окружности с постоянной скоростью происходит под действием направленной к центру (центростремительной) силы. В нашем случае в качестве центростремительной выступает сила Лоренца F. Из механики известно, что центростремительная сила может быть рассчитана по формуле:
,
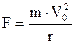
где r – радиус окружности вращения электрона. Приравняв центростремительную силу, получаемую из последнего выражения к выражению для силы Лоренца, получим:
.
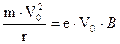
Откуда найдем радиус:
.
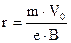
Чем больше скорость электрона, тем больше и радиус окружности, описываемой им в магнитном поле. Выйдя за пределы магнитного поля, электрон летит равномерно и прямолинейно по инерции. Если же радиус окружности мал, то электрон может описывать в магнитном поле замкнутые окружности.
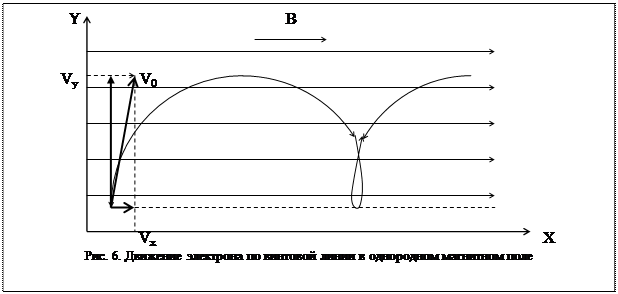
Результирующее движение электрона происходит по винтовой линии (по спирали). В зависимости о значений B, Vx и Vy, эта спираль более или менее растянута. Радиус спирали легко определить по последней формуле, подставив в нее скорость Vy.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Движение электрона в магнитном поле по окружности
В некоторых электронных приборах используется влияние магнитного поля на движущиеся в нем электроны.
В § 3-2, в было получено выражение (3-6) для силы, с которой однородное магнитное поле действует на электрон, движущийся перпендикулярно направлению поля. Величина этой силы пропорциональна произведению магнитной индукции В, заряда электрона 
и скорости его движения v в направлении, перпендикулярпом направлению поля, т. е. 
Там же было установлено, что направление этой силы определяется по правилу левой руки.
Из выражения силы (3-6) следует, что при 
сила 
, т. е. магнитное поле на неподвижный электрон не действует. Так как направление силы F перпендикулярно направлению скорости движения электрона, то работа, совершаемая ею, равна нулю. Таким образом, энергия электрона и величина его скорости остаются неизменными, а изменяется только направление движения электрона.
Если на электрон действует только магнитное поле, то он будет перемещаться по окружности радиуса 
(рис. 13-4), расположенной в плоскости, перпендикулярной направлению ноля.
Сила F является центростремительной и уравновешивается центробежной силой электрона 
.
Так как эти силы равны, то можно написать
откуда определяется радиус, окружности
Отношение массы электрона к его заряду постоянно, следовательно, радиус окружности пропорционален скорости движения электрона и обратно пропорционален магнитной индукции поля.
Рис. 13-4. Движение электрона в магнитном поле при начальной скорости v в плоскости, перпендикулярной вектору магнитной индукции поля.
Рис. 13-5. Движение электрона в магнитном поле при начальной скорости, направленной под острым углом к вектору магнитной индукции поля.
Если начальная скорость электрона не перпендикулярна направлению поля, то ее следует разложить на две составляющие: нормальную, т. е. перпендикулярную к направлению поля 
и продольную, т. е. совпадающую по направлению с полем 
(рис. 13-5).
Первая составляющая скорости 
обусловливает движение электрона по окружности в плоскости, перпендикулярной к направлению поля, вторая составляющая 
обусловливает равномерное и прямолинейное движение электрона в направлении поля, таким образом, движение электрона происходит по винтовой линии (рис. 13-5).
Физика. 10 класс
§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).
Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:
где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑
Физика. 10 класс
§ 30. Сила Лоренца. Движение заряженных частиц в магнитном поле
Поскольку электрический ток представляет собой упорядоченное движение заряженных частиц, то это означает, что магнитное поле, действуя на проводник с током, действует тем самым на каждую из этих частиц. Таким образом, силу Ампера можно рассматривать как результат сложения сил, действующих на отдельные движущиеся заряженные частицы. Как можно определить силу, действующую со стороны магнитного поля на заряженную частицу, движущуюся в этом поле?
Сила Лоренца. Силу, которой магнитное поле действует на заряженную частицу, движущуюся в этом поле, называют силой Лоренца в честь выдающегося нидерландского физика Хендрика Антона Лоренца ( 1853–1928 ).
Поскольку – модуль средней скорости упорядоченного движения заряженной частицы в стационарном * электрическом поле внутри проводника, то формулу для определения модуля силы Лоренца можно записать в виде:
где α — угол между направлениями индукции магнитного поля и скорости упорядоченного движения заряженной частицы.
Из формулы (30.1) следует, что сила Лоренца максимальна в случае, когда заряженная частица движется перпендикулярно направлению индукции магнитного поля (α = 90°). Когда частица движется вдоль линии индукции поля (α = 0° или α = 180°), сила Лоренца на неё не действует. Сила Лоренца зависит от выбора инерциальной системы отсчёта, так как в разных системах отсчёта скорость движения заряженной частицы может отличаться.
Направление силы Лоренца, действующей на заряженную частицу, как и направление силы Ампера, определяют по правилу левой руки (рис. 168): если левую руку расположить так, чтобы составляющая индукции магнитного поля, перпендикулярная скорости движения частицы, входила в ладонь, а четыре пальца были направлены по движению положительно заряженной частицы (против движения отрицательно заряженной частицы), то отогнутый на 90° в плоскости ладони большой палец укажет направление действующей на частицу силы Лоренца.
Сила Лоренца перпендикулярна как направлению скорости движения частицы, так и направлению индукции магнитного поля.
* Электрическое поле, создаваемое и поддерживаемое источником тока в течение длительного промежутка времени и обеспечивающее постоянный электрический ток в проводнике, называют стационарным электрическим полем. ↑