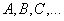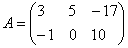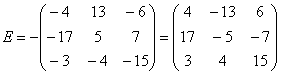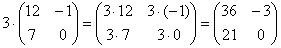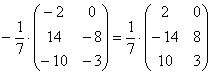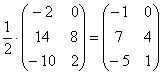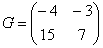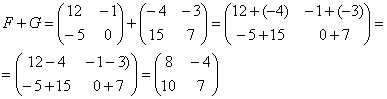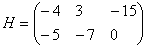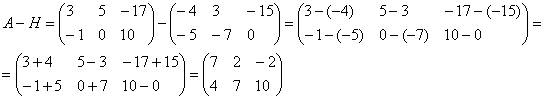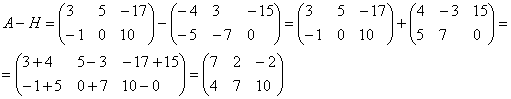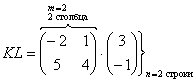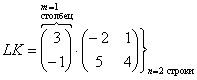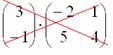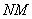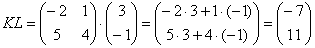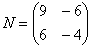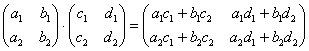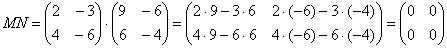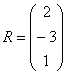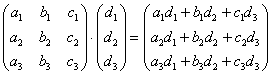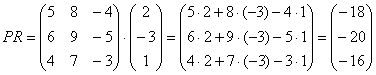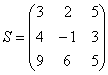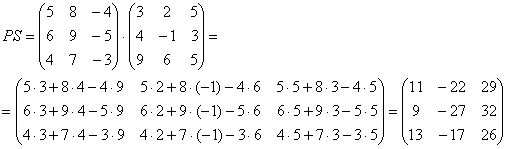Как поделить матрицу на число

Действия с матрицами

Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.

Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.

Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!

Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.

Обозначение: матрицы обычно обозначают прописными латинскими буквами

Пример: рассмотрим матрицу «два на три»:

Данная матрица состоит из шести элементов: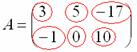

Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: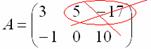

Это просто таблица (набор) чисел!

Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!

Рассматриваемая матрица имеет две строки: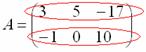

и три столбца:

СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».

Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: 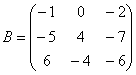– матрица «три на три».

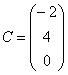
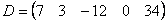
Если в матрице один столбец или одна строка , то такие матрицы также называют векторами.

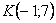
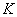
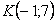
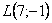
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: . По существу, координаты точки записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: и – это две совершенно разные точки плоскости.

Теперь переходим непосредственно к изучению действий с матрицами:

1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).

Вернемся к нашей матрице 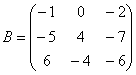. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.

Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: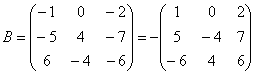

У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.

Обратный пример: 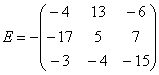. Выглядит безобразно.

Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:

Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.

2) Действие второе. Умножение матрицы на число.

Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.

Еще один полезный пример:

– умножение матрицы на дробь

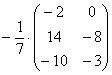
Сначала рассмотрим то, чего делать НЕ НАДО: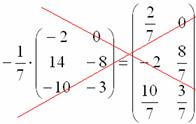

Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если 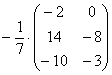– окончательный ответ задания).

И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:

Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.

Единственное, что желательно сделать в этом примере – это внести минус в матрицу:

А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В этом случае можно и НУЖНО умножить все элементы матрицы на 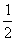, так как все числа матрицы делятся на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

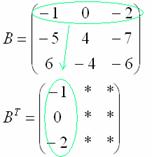
3) Действие третье. Транспонирование матрицы.

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

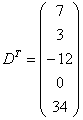
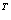
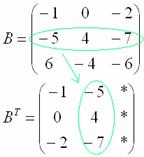
Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Транспонировать матрицу

Сначала переписываем первую строку в первый столбец:

Потом переписываем вторую строку во второй столбец:

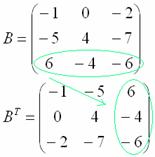
И, наконец, переписываем третью строку в третий столбец:

Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Сложить матрицы 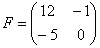и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

Найти разность матриц ,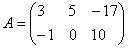

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :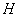

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

5) Действие пятое. Умножение матриц.

Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.

Какие матрицы можно умножать?

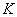
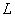
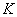
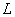
Чтобы матрицу можно было умножить на матрицу нужно, чтобы число столбцов матрицы равнялось числу строк матрицы .

Пример:
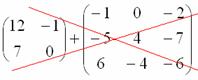
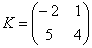
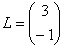
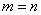
Можно ли умножить матрицу на матрицу ?

, значит, умножать данные матрицы можно.

А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!

, следовательно, выполнить умножение невозможно:

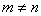
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.

Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
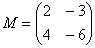
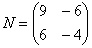
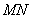
Например, для матриц, и возможно как умножение , так и умножение

Как умножить матрицы?

Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.

Начнем с самого простого:

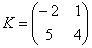
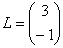
Умножить матрицу на матрицу
Я буду сразу приводить формулу для каждого случая:

– попытайтесь сразу уловить закономерность.

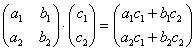
Умножить матрицу 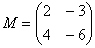на матрицу

Формула:

В результате получена так называемая нулевая матрица.

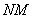
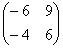
Попробуйте самостоятельно выполнить умножение (правильный ответ ).

Обратите внимание, что 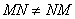! Это почти всегда так!

Таким образом, при умножении переставлять матрицы нельзя!

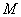
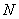
Если в задании предложено умножить матрицу на матрицу , то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.

Переходим к матрицам третьего порядка:

Умножить матрицу 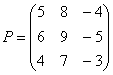на матрицу

Формула очень похожа на предыдущие формулы:

А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:

Умножьте матрицу 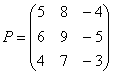на матрицу

Вот готовое решение, но постарайтесь сначала в него не заглядывать!

Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.

А пока спектакль закончен.

После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Операции над матрицами: сложение, вычитание, умножение, деление, возведение в степень.
Вычисление определителя матрицы, обратной матрицы, ранга матрицы.

С помощью данной математической программы вы сможете выполнить основные операции над матрицами.

Программа не только даёт ответ, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ или вузов при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

Сложение и вычитание матриц
При сложении и вычитании матриц их размеры должны быть одинаковыми.
Это значит что при вычислении \( A \pm B \) кол-во строк и столбцов матриц \( A \) и \( B \) должно быть одинаковым.

Умножение матриц
При умножении матриц \( A \cdot B \) кол-во столбцов \(A\) должно быть равно кол-ву строк \(B\)

Для вычисления \( A^n \) показатель степени \(n\) должен быть целым числом.

Если в вычислениях используется только одна матрица, то вторую можно не вводить. RND CFracNum Fill RND int Fill
Сюда ввести строку с GET параметрами :

Немного теории.

Матрицы и операции над ними

Виды матриц

Как правило, их обозначают строчной буквой с двумя индексами, например \(a_\), где \(i\) — номер строки ( \(i=\overline <1,m>\) ), \(j\) — номер столбца ( \(j=\overline <1,n>\) ), в которых расположен этот элемент.

Матрицу записывают так:
$$ \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end $$

Если по тексту ясно, в каких пределах изменяются индексы \(i\) и \(j\), то сокращённо матрицу можно записать так: \( \left(a_ \right) \). Матрицу как единый объект обозначают прописной буквой: \(A\), \(B\) и т.д.

Элементами матриц могут быть не только действительные числа, но и комплексные, и даже другие математические объекты. Например, элементами матриц могут быть многочлены или матрицы.

Матрицу называют матрицей-столбцом, если матрица имеет размер \(m \times 1 \), т.е. если у матрицы один столбец. Число элементов в матрице-столбце называют её высотой.
\(A = \begin a_ <1>\\ \vdots \\ a_ \\ \end \)

Матрицу называют квадратной порядка \(n\), если \( m=n\), т.е. когда матрица имеет столько же столбцов, сколько и строк :
$$ \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end $$ а если \(m \neq n \) — прямоугольной.

Матрицу размера \(m \times n \), все элементы которой равны нулю, называют нулевой матрицей соответствующего размера и обозначают буквой \(\Theta\) или цифрой 0.

Часто используют матрицы и других видов, например верхние треугольные матрицы
$$ \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ 0 & a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & a_ \\ \end $$
у которых элементы, расположенные под главной диагональю, равны нулю, и нижние треугольные матрицы, у которых, наоборот, элементы над главной диагональю равны нулю:
$$ \begin a_ <11>& 0 & \cdots & 0 \\ a_ <21>& a_ <22>& \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end $$

Линейные операции над матрицами

Определение 2.
Две матрицы называют равными, если они имеют один и тот же размер и если у них совпадают соответствующие элементы.

Определение 3.
Суммой матриц \( A=(a_) \) и \( B=(b_) \) размера \(m \times n \) называют матрицу \( C=(c_) \) того же размера с элементами \( c_ = a_ + b_, \; i=\overline <1,m>, \; j=\overline <1,n>\)

В подробной записи:
\( A+B = \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end + \) \( \begin b_ <11>& b_ <12>& \cdots & b_ <1n>\\ b_ <21>& b_ <22>& \cdots & b_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ b_ & b_ & \cdots & b_ \\ \end = \) \( \begin a_<11>+b_ <11>& a_<12>+b_ <12>& \cdots & a_<1n>+b_ <1n>\\ a_<21>+b_ <21>& a_<22>+b_ <22>& \cdots & a_<2n>+b_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_+b_ & a_+b_ & \cdots & a_+b_ \\ \end = C \)

Сумма определена только для матриц одного размера.

Определение 4.
Произведением матрицы \( A=(a_) \) размера \(m \times n \) на число \( k \in \mathbb\) называют матрицу \( C=(c_) \) размера \(m \times n \) с элементами \( c_ = k \cdot a_ \).
Подробно это произведение выглядит так:
\( k \cdot \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end = \) \( \begin k \cdot a_ <11>& k \cdot a_ <12>& \cdots & k \cdot a_ <1n>\\ k \cdot a_ <21>& k \cdot a_ <22>& \cdots & k \cdot a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ k \cdot a_ & k \cdot a_ & \cdots & k \cdot a_ \\ \end \)

Замечание. Операции сложения и умножения на число для матриц аналогичны одноименным операциям над векторами. Эти операции также называют линейными.

Свойства линейных операций над матрицами

1. Сложение матриц коммутативно: \( A+B = B+A \)

2. Сложение матриц ассоциативно: \( (A+B)+C = A+(B+C) \)

3. Умножение матрицы на число ассоциативно: \( (\lambda \mu ) A = \lambda (\mu A) \)

4. Умножение матрицы на число дистрибутивно относительно суммы действительных чисел: \( (\lambda + \mu)A = \lambda A + \mu A \)

5. Умножение матрицы на число дистрибутивно относительно суммы матриц: \( \lambda(A + B) = \lambda A + \lambda B \)

Транспонирование матриц

Определение 5.
Для матрицы \( A=(a_) \) размера \(m \times n \) её транспонированной матрицей называют матрицу \( A^T=(c_) \) размера \(m \times n \) с элементами \( c_ = a_ \).

При транспонировании матрицы её строки становятся столбцами новой матрицы с сохранением их порядка. Точно так же столбцы исходной матрицы превращаются в строки транспонированной. Поэтому транспонирование можно рассматривать как преобразование симметрии матрицы относительно её главной диагонали.
Подробнее:
\( \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end ^T = \) \( \begin a_ <11>& a_ <21>& \cdots & a_ \\ a_ <12>& a_ <22>& \cdots & a_ \\ \vdots & \vdots & \ddots & \vdots \\ a_ <1n>& a_ <2n>& \cdots & a_ \\ \end \)

Свойства операции транспонирования

1. \( \left( A^T \right) ^T = A \)

2. \( \left( A+B \right) ^T = A^T + B^T \)

4. \( (A \cdot B)^T = B^T \cdot A^T \)

5. \( |A| = \left| A^T \right| \) При транспонировании определитель матрицы не меняется.

Умножение матриц

Определение 6.
Пусть даны матрица \( A=(a_) \) размера \(m \times n \) и матрица \( B=(b_) \) размера \(n \times p \). Произведением матриц \(A\) и \(B\) называют матрицу \( C=(c_) \) размера \(m \times p \) с элементами
$$ c_ = \sum_^n a_ b_ $$
которую обозначают \( C = AB\).

Произведение определено лишь в том случае, когда количество столбцов первого сомножителя равно количеству строк второго. В формировании элемента \(c_\) произведения \(AB\) участвуют элементы \(i\)-й строки матрицы \(A\) и \(j\)-го столбца матрицы \(B\). Поэтому правило умножения матриц называют также правилом умножения «строка на столбец»:

Иллюстрации умножения матриц :

Таким образом, произведение любой матрицы-строки и любой матрицы-столбца, имеющих одинаковое количество элементов, есть число, равное сумме произведений их элементов с одинаковыми индексами. Если матрица-строка и матрица-столбец имеют разное количество элементов, то их перемножить нельзя.

Чтобы матрицу \(A\) размера \(m \times n \) можно было умножить на матрицу \(B\) и слева, и справа (т.е. чтобы были определены оба произведения \(BA\) и \(AB\) ), матрица \(B\) должна иметь размер \(n \times m \).

Свойства умножения матриц

1. Умножение матриц ассоциативно: \( (AB)C = A(BC) \)

2. Умножение матриц дистрибутивно относительно сложения матриц: \( (A+B)C = AC+BC \)

3. Для любых матриц \(A\) и \(B\) размеров \(m \times n \) и \(n \times k \) выполнено равенство \( (AB)^T = B^T A^T \), т.е. транспонированное произведение двух матриц равно произведению в обратном порядке транспонированных матриц.

4. В общем случае умножение матриц не коммутативно, т.е. \( AB \neq BA \)

Операция умножения матриц позволяет ввести операцию возведения квадратной матрицы в натуральную степень.
\(A^0 = E \), где \(E\) — единичная матрица того же порядка.
\( A^1 = A, \;\; A^ = AA^n, \;\; n=1,2. \)
Отметим, что две степени \(A^n\) и \(A^m\) одной и той же матрицы являются матрицами одного порядка и перестановочны: \(A^nA^m = A^mA^n = A^\).

Элементарные преобразования матриц

1. Умножение строки матрицы на число не равное нулю.

2. Перестановка двух строк матрицы.

3. Суммирование одной строки с другой строкой, умноженной на число.

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов.

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование, которое преобразованную матрицу превращает в исходную.

Теорема. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду.

Определители

Определители n-го порядка

Транспозицией перестановки называют такое её преобразование, при котором в ней меняются местами какие-либо два элемента, а другие остаются на своих местах.

Теорема. Любая транспозиция меняет четность перестановки.

Подстановку называют четной, если перестановки, из которых она состоит, имеют одинаковую четность, и нечетной в противоположном случае.
Четность подстановки \( (1) \) совпадает с четностью числа \( |\beta|+|\alpha| \) — общего количества инверсий в строках подстановки, которое обозначают \( |\sigma| \).

Транспозицией подстановки называют любую перестановку её столбцов. Поскольку транспозиция подстановки вызывает транспозиции и в образующих её перестановках, то, согласно предыдущей теореме, очевидно, что транспозиция подстановки не меняет её четность.

Соглашение о равенстве подстановок позволяет записать любую подстановку так, чтобы первая строка являлась нормальной перестановкой. Поэтому различных подстановок \(n\)-й степени имеется ровно \(n!\)

Определение. Определителем порядка \(n\), соответствующим квадратной матрице
\( A = \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end \tag <2>\) порядка \(n\) (определителем квадратной матрицы порядка \(n\) ), называют сумму \(n!\) слагаемых
$$ \large |A| = \sum_ <\sigma>(-1)^ <|\sigma|>a_ <1\alpha_1>a_ <2\alpha_2>. a_ \tag <3>$$ которая берется по всевозможным подстановкам вида
\( \sigma = \begin 1 & 2 & \cdots & n \\ \alpha_1 & \alpha_2 & \cdots & \alpha_n \end \)

Определитель матрицы \(A\) часто называют просто определителем, или детерминантом, и обозначают
\( \begin a_ <11>& a_ <12>& \cdots & a_ <1n>\\ a_ <21>& a_ <22>& \cdots & a_ <2n>\\ \vdots & \vdots & \ddots & \vdots \\ a_ & a_ & \cdots & a_ \\ \end \)
или \( \det A\), называя \(A\) матрицей этого определителя.

Свойства определителей

Поскольку определители соответствуют квадратным матрицам, в их теорию легко переносится матричная терминология (порядок, элементы, строки, столбцы, диагональ, диагональные элементы, виды матриц и определителей, транспонирование, элементарные преобразования строк и столбцов, линейные комбинации строк и столбцов и др.).
При изучении определителей используют эту возможность, подразумевая однако, что терминология относится к матрице определителя.

Свойство 1. Определитель не меняется при транспонировании, т.е. \( |A| = \left| A^T \right| \)

Свойство 2. При перестановке двух строк (столбцов) определитель меняет свой знак на противоположный.

Свойство 3. Если все элементы \(j\)-го столбца определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все столбцы, кроме \(j\)-го, такие же, как и в данном определителе, а \(j\)-й столбец первого определителя состоит из первых слагаемых \(j\)-го столбца данного определителя, а второго — из вторых слагаемых :
\( \begin a_ <11>& \cdots & \alpha_ <1j>+ \beta_ <1j>& \cdots & a_ <1n>\\ a_ <21>& \cdots & \alpha_ <2j>+ \beta_ <2j>& \cdots & a_ <2n>\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_ & \cdots & \alpha_ + \beta_ & \cdots & a_ \end = \) \( \begin a_ <11>& \cdots & \alpha_ <1j>& \cdots & a_ <1n>\\ a_ <21>& \cdots & \alpha_ <2j>& \cdots & a_ <2n>\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_ & \cdots & \alpha_ & \cdots & a_ \end + \) \( \begin a_ <11>& \cdots & \beta_ <1j>& \cdots & a_ <1n>\\ a_ <21>& \cdots & \beta_ <2j>& \cdots & a_ <2n>\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ a_ & \cdots & \beta_ & \cdots & a_ \end \) Аналогично для строки.

Свойство 4. Общий множитель элементов строки или столбца может быть вынесен за знак определителя.
Для умножения определителя на число достаточно умножить на это число элементы любой строки или любого столбца.

Свойство 5. Определитель равен нулю, если он имеет :
1) нулевую строку (столбец)
2) хотя бы две одинаковые строки (столбца)
3) хотя бы две строки (столбца), элементы которых пропорциональны
4) хотя бы одну строку (столбец), являющуюся линейной комбинацией других строк (столбцов).

Свойство 6. Определитель не изменится, если к любой его строке (столбцу) прибавить другую строку (столбцец), умноженную на число.

В матрице \(A\) вычеркнем \(i\)-ю строку и \(j\)-й столбец, в которых стоит элемент \(a_\). Из оставшихся элементов можно составить новую квадратную матрицу (n-1)-го порядка, сдвинув строки и столбцы после вычеркивания.
Определитель построенной матрицы обозначают через \( M_ \) и называют минором (матрицы \(A\) и её определителя \(\Delta\) ), соответствующим элементу \(a_\).
Число \( A_= (-1)^ M_ \) называют алгебраическим дополнением, соответствующим этому же элементу \(a_\).

Миноры и алгебраические дополнения позволяют, в частности, вычислять определитель n-го порядка путем сведения его к вычислению n определителей (n-1)-го порядка.

Разложения по строке (4) и столбцу (5) дают правила, в соответствии с которыми определитель n-го порядка сводится к n определителям (n-1)-го порядка, раскладывая которые получим n(n-1) определителей (n-2)-го порядка и т.д.
Эти вычисления получаются громоздкими, однако процесс упрощается, если среди элементов определителя имеется много нулей. Целесообразно раскладывать определитель по тому ряду (строке, столбцу), в котором больше нулей.
Если же в этом смысле некоторые ряды одинаковы, то удобнее выбирать тот из них, в котором элементы имеют большие значения по абсолютной величине, поскольку это упрощает выполнение арифметических вычислений.

С помощью элементарных преобразований строк любая матрица приводится к ступенчатому виду. Квадратная матрица ступенчатого вида является частным случаем верхней треугольной матрицы, у которой диагональные элементы, начиная с некоторого, могут быть равны нулю. Определитель такой матрицы легко найти по свойству 8. В алгоритме приведения к ступенчатому виду используется перестановка строк, при которой определитель матрицы меняет знак. Изменение знака можно учесть, например, дополнительным умножением определителя или одной из строк на —1. Следовательно, квадратную матрицу всегда можно привести элементарными преобразованиями строк к верхнему треугольному виду с сохранением значения её определителя.

Свойство 9. Определитель произведения двух квадратных матриц A, B равен произведению их определителей, т.е. \( |АВ| = |A||B| \).

Свойство 10. Определитель обратной матрицы: \( \left| А^ <-1>\right| = \frac<1> <|A|>\)

Свойство 11. Если матрица \(A\) порядка \(n\), то \( |kA|=k^n|A| \)

Вычисление определителя для частных случаев матриц

Определитель единичной матрицы равен 1 : \( |E| = 1 \)

Определитель матрицы 1-го порядка равен единственному элементу этой матрицы : \( |a_<11>| = a_ <11>\)

Вычисление определителя для матрицы 2-го порядка.
\( \Delta = \begin a & c \\ b & d \end = ad-bc \)

Обратная матрица и её свойства

Определение. Пусть \(A\) — квадратная матрица порядка \(n\). Квадратную матрицу \(B\) того же порядка называют обратной к \(A\), если \( AB= BA =E \), где \(E\) — единичная матрица порядка \(n\).

Обратную матрицу обозначают \(A^<-1>\). Она позволяет определить целую отрицательную степень матрицы \(A\).
А именно, для \(n>0\) полагают \(A^ <-n>= \left( A^ <-1>\right)^n \).

Свойство. Если квадратная матрица \(A\) имеет обратную матрицу, то обратная матрица единственная.

Квадратная матрица не всегда имеет обратную. Установить, имеет ли данная матрица обратную, позволяет следующая теорема.

Свойство. Для того чтобы квадратная матрица \(A\) порядка \(n\) имела обратную, необходимо и достаточно, чтобы \(|A| \neq 0 \).

Следствие. Если квадратная матрица \(A\) имеет обратную, то \( \left| А^ <-1>\right| = \frac<1> <|A|>\)

Квадратную матрицу с ненулевым определителем называют невырожденной или неособой. В противном случае, когда определитель матрицы равен нулю, её называют вырожденной. Итак, для существования обратной матрицы \(A^<-1>\) необходимо и достаточно, чтобы сама матрица \(A\) была невырожденной.

Свойство. Если квадратные матрицы \(A\) и \(B\) порядка \(n\) имеют обратные матрицы, то и их произведение имеет обратную матрицу, причем \( \left( AB \right)^ <-1>= B^<-1>A^ <-1>\)

Свойство. Если матрица \(A\) порядка \(n\) имеет обратную, то и транспонированная матрица \(A^T\) имеет обратную, причем \( \left( A^T \right)^ <-1>= \left( A^ <-1>\right)^T \)

Вычисление обратной матрицы

С помощью матрицы алгебраических дополнений

Таким образом, чтобы для квадратной матрицы порядка n найти обратную матрицу, надо вычислить один определитель порядка n и составить транспонированную матрицу алгебраических дополнений к матрице \(A\), т.е. вычислить \(n^2\) определителей порядка n-1.
Метод присоединенной матрицы эффективен при \(n=2\) или \(n=3\), но при росте n становится слишком трудоемким.

Отметим, что для квадратной матрицы \(A\) 2-го порядка присоединенная матрица \(M^T\) получается перестановкой в \(A\) диагональных элементов и изменением знака двух других.

С помощью метода Жордана-Гаусса

Этот метод состоит в преобразовании исходной матрицы к более простому виду с помощью элементарных преобразований строк.
Чтобы найти матрицу \(A^<-1>\), обратную к \(A\), фактически надо решить матричное уравнение \(AX=E\).
Отметим, что если над матрицей \(A\) выполняется какое-либо элементарное преобразование строк, то это же преобразование осуществляется и над матрицей \(AX\), поскольку любое элементарное преобразование строк матрицы эквивалентно умножению её слева на соответствующую матрицу специального вида. Таким образом, если в уравнении \(AX=E\) над матрицами \(A\) и \(E\) одновременно выполнить какое-либо элементарное преобразование строк, т.е. домножить это равенство слева на некоторую матрицу специального вида, то в результате получится новое матричное уравнение \(A_1X=B_1\). Оба эти матричные уравнения имеют одно и то же решение, так как любое элементарное преобразование строк имеет обратное элементарное преобразование строк.
Последовательность элементарных преобразований строк надо подобрать так, чтобы на s-м шаге матрица \(A\) превратилась в единичную матрицу.
В результате этих s шагов получается уравнение \(A_sX=B_s\), где \(A_s=E\), т.е. \(X=B_s\). Итак, поскольку \(A^<-1>\) является решением уравнения \(AX=E\), которое эквивалентно \(X=B_s\), то \(A^<-1>=B_s\).

Чтобы синхронно выполнять преобразования над матрицами в левой и правой частях матричного уравнения \(AX=E\), записывают блочную матрицу \( (A|E)\) и выполняют такие элементарные преобразования строк этой матрицы, чтобы вместо \(A\) получить единичную матрицу \(E\), тогда на месте \(E\) получится нужная матрица \(A^<-1>\).

Ранг матрицы

Для ранга матрицы \(A\) используют обозначение \(\textA\).

Если квадратная матрица порядка n невырождена, то её ранг равен её порядку n : ненулевым является единственный минор максимального порядка n, совпадающий с определителем матрицы.
В частности, ранг единичной матрицы \(E\) порядка n равен n.

Если квадратная матрица вырождена, то её ранг меньше её порядка : единственный минор максимального порядка, равного порядку матрицы, является нулевым, и в этом случае ненулевые миноры имеют меньший порядок.
Ранг нулевой матрицы полагают равным нулю.

Ранг диагональной матрицы равен количеству её ненулевых диагональных элементов.

Непосредственно из определения ранга матрицы следует, что ранг имеет следующее свойство, полностью его характеризующее.

Свойство. Если ранг матрицы равен \(r\), то матрица имеет хотя бы один минор порядка \(r\), не равный нулю, а все её миноры больших порядков равны нулю.

Теорема. При транспонировании матрицы её ранг не меняется, т.е. \( \text A^T = \text A \)

Теорема. Ранг матрицы не меняется при элементарных преобразованиях её строк и столбцов.

Теорема о базисном миноре

Среди миноров матрицы могут быть как равные нулю, так и отличные от нуля.

Определение.
Минор \(M\) матрицы \(M\) называют базисным, если выполнены два условия:
1) он не равен нулю
2) его порядок равен рангу матрицы А

Матрица \(A\) может иметь несколько базисных миноров. Строки и столбцы матрицы \(A\), в которых расположен выбранный базисный минор, называют базисными.

Теорема о базисном миноре. Базисные строки (столбцы) матрицы \(A\), соответствующие любому её базисному минору \(M\), линейно независимы. Любые строки (столбцы) матрицы \(A\), не входящие в \(M\), являются линейными комбинациями базисных строк (столбцов).

Следствие. Для того чтобы квадратная матрица была невырожденной, необходимо и достаточно, чтобы её строки (столбцы) были линейно независимы.

Теорема. Линейно независимые строки (столбцы) матрицы, количество которых равно рангу матрицы, являются базисными строками (столбцами).

Теорема. Для любой матрицы её ранг равен максимальному количеству её линейно независимых строк (столбцов).

Следствие. Для любой матрицы максимальное число линейно независимых строк равно максимальному числу линейно независимых столбцов.

Вычисление ранга матрицы

Метод окаймляющих миноров

Минор \(M’\) матрицы \(A\) называют окаймляющим для минора \(M\), если он получается из последнего добавлением одной новой строки и одного нового столбца матрицы \(A\).
Ясно, что порядок окаймляющего минора \(M’\) на единицу больше, чем порядок минора \(M\).

Метод окаймляющих миноров позволяет найти один из базисных миноров матрицы и состоит в следующем.
Выбирается ненулевой минор первого порядка (ненулевой элемент матрицы). К очередному ненулевому минору последовательно добавляются такие строка и столбец, чтобы новый окаймляющий минор оказался ненулевым. Если этого сделать нельзя, то последний ненулевой минор является базисным (что утверждает следующая ниже теорема). Этот процесс рано или поздно закончится из-за ограниченных размеров матрицы.

Теорема. Если для некоторого минора матрицы все окаймляющие его миноры равны нулю, то он является базисным.

Метод элементарных преобразований

При элементарных преобразованиях строк (столбцов) матрицы её ранг не меняется. С помощью этих преобразований можно так упростить матрицу, чтобы ранг новой матрицы легко вычислялся.

Например с помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду. Ранг же ступенчатой матрицы равен количеству ненулевых строк. Базисным в ней является минор, расположенный на пересечении ненулевых строк со столбцами, соответствующими первым слева ненулевым элементам в каждой из строк. Действительно, этот минор ненулевой, так как соответствующая матрица является верхней треугольной, а любое его окаймление содержит нулевую строку. Поэтому приведение матрицы к ступенчатому виду с помощью элементарных преобразований строк позволяет вычислить ранг матрицы.

Приведенные два метода существенно отличаются друг от друга.
При нахождении ранга конкретной матрицы методом окаймляющих миноров может потребоваться большое количество вычислений. Это связано с тем, что метод требует вычисления определителей, порядок которых может возрасти до минимального из размеров матрицы. Однако в результате будет найден не только ранг матрицы, но и один из её базисных миноров.

При нахождении ранга матрицы методом элементарных преобразований требуется гораздо меньше вычислений. Причем разница в объемах вычислений возрастает с ростом размеров матрицы и усложнением её вида. Но этот метод позволяет найти базисный минор лишь для матрицы ступенчатого вида, полученной в результате элементарных преобразований. Чтобы найти базисный минор исходной матрицы, нужны дополнительные вычисления с учетом уже известного ранга матрицы.

Источник