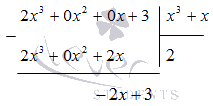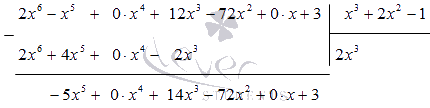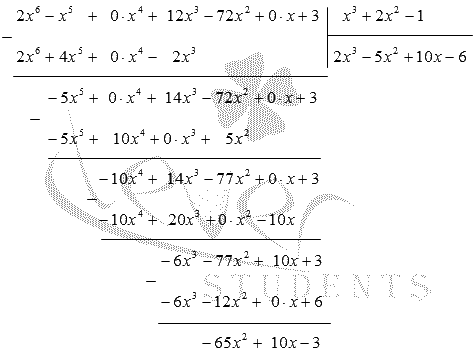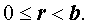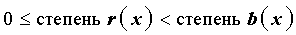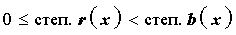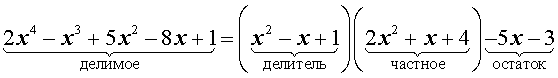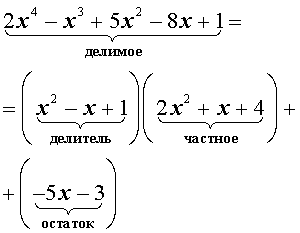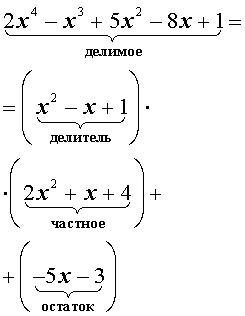Как поделить многочлен на многочлен уголком
Деление многочлена на многочлен «уголком»
Пример:
\(6x^2+6+x^3+11x\) записываем как \(x^3+6x^2+11x+6\)
1) Подбором найдите один из корней многочлена.
Для этого вместо \(x\) подставьте по очереди числа: \(±1,±2,±3,±4,±5\) и т.д. Число, которое сделает многочлен нулем и будет его корнем.
Матхак! Пробуйте сначала числа, на которые свободный член делиться нацело. В данном случае свободный член \(6\), поэтому в первую очередь нужно пробовать числа: \(±1,±2,±3\) и \(±6\).
а) Запишите многочлены как числа при делении столбиком:
б) Подберите такой одночлен, чтобы при умножении его на \(x\), получалось первое слагаемое исходного многочлена, то есть в нашем случае \(x^3\). Очевидно, что таким одночленом будет \(x^2\).
в) Умножьте этот одночлен на делитель и запишите результат под исходным многочленом. Таким образом, мы умножаем \(x^2\) на \(x+1\) и получаем \(x^3+x^2\).
г) Теперь точно так же, как в случае деления натуральных чисел, поставьте знак минус, проведите горизонтальную черту и сделайте вычитание.
д) Повторите шаги б) – г) только уже с новым многочленом:
— подберите такой одночлен, чтобы при умножении на \(x\) первое слагаемое было таким же, как в новом многочлене: в нашем примере этим одночленом будет \(5x\).
— умножьте этот одночлен на делитель: умножив \(5x\) на \(x+1\) получим \(5x^2+5x\).
— вычтите получившиеся многочлены:
е) И вновь повторяем шаги б) – г) до тех пор, пока после вычитания не останется ноль.
3) Запишите новый вид многочлена, представив его как произведение делителя и частного.
\(x^3+6x^2+11x+6=(x+1)(x^2+5x+6)\)
Матхак! Если есть сомнения в правильности разложения, можно проверить его раскрытием скобок – в результате должен получиться исходный многочлен.
Проверим наш случай: \((x+1)(x^2+5x+6)=x^3+5x^2+6x+x^2+5x+6=x^3+6x^2+11x+6\).
Получен исходный многочлен, значит, поделили правильно.
Матхак! Если в результате деления у вас в остатке получился не ноль, значит, скорее всего, в решении есть ошибка.
Давайте теперь решим пример с применением изученного материала.
Пример: Решите неравенство \(x^4-3x^3+6x-4≥0\).
Найдем один из корней многочлена слева. Проверим \(1\).
Поделим многочлен \(x^4-3x^3+6x-4\) на \((x-1)\) уголком. Однако замечаем, что у нас нет слагаемого с квадратом. Чтоб нам было удобнее решать, запишем вместо него выражение \(0·x^2\) (ведь его значение равно нулю, а значит оно ничего не меняет в исходном многочлене).
Запишем новый вид нашего неравенства.
Теперь выносим общую скобку \((x-2)\) за скобку.
Деление многочленов
В данной статье будут рассмотрены рациональные дроби, ее выделения целых частей. Дроби бывают правильными и неправильными. Когда в дроби числитель меньше знаменателя – это правильная дробь, а неправильная наоборот.
При выделении целой части производится процесс деления числителя на знаменатель. Тогда такая дробь может быть представлена как сумма целой и дробной части, где дробная считается отношением остатка от деления и знаменателя.
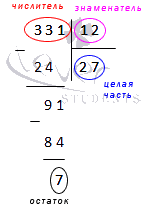
Необходимо произвести деление столбиком, тогда получим, что
Значит, 27 4 = ц е л а я ч а с т ь + о с т а т о к з н а м е н а т е л ь = 6 + 3 4
Производим деление знаменателя на числитель при помощи уголка:
Производим деление далее и получаем, что
Вторая дробь является правильной, значит, целая часть равняется нулю.
Рассмотрим классификацию многочленов, иначе говоря, дробно-рациональную функцию. Ее считают правильной, когда степень числителя меньше степени знаменателя, иначе ее считают неправильной.
Деление многочлена на многочлен происходит по принципу деления углом, а представление функции как сумма целой и дробной частей.
Чтобы разделить многочлен на линейный двучлен, используется схема Горнера.
Воспользовавшись свойством деления, запишем, что
Зачастую такого вида преобразования выполняются при взятии интегралов.
Степень числителя больше, чем у знаменателя, значит, что у нас имеется неправильная дробь. При помощи деления столбиком выдели целую часть. Получаем, что
Произведем деление еще раз и получим:
Существуют случаи, где необходимо дополнительно выполнять преобразование дроби для того, чтобы можно было выявить остаток при делении. Это выглядит следующим образом:
8 x 3 + 36 x 2 + 54 x + 27 2 x + 3 = ( 2 x + 3 ) 3 2 x + 3 = ( 2 x + 3 ) 2 = 4 x 2 + 12 x + 9
Заданный многочлен делится без остатка.
Для решения используется более удобный метод решения, причем деление многочлена на многочлен считается максимально универсальным, поэтому часто используемым при выделении целой части. Итоговая запись должна содержать полученный многочлен от деления.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
С помощью данной математической программы вы можете поделить многочлены столбиком.
Программа деления многочлена на многочлен не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вам нужно или упростить многочлен или умножить многочлены, то для этого у нас есть отдельная программа Упрощение (умножение) многочлена
Немного теории.
Деление многочлена на многочлен (двучлен) столбиком (уголком)
В алгебре деление многочленов столбиком (уголком) — алгоритм деления многочлена f(x) на многочлен (двучлен) g(x), степень которого меньше или равна степени многочлена f(x).
Алгоритм деления многочлена на многочлен представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Для любых многочленов \( f(x) \) и \( g(x) \), \( g(x) \neq 0 \), существуют единственные полиномы \( q(x) \) и \( r(x) \), такие что
$$ \frac
причем \( r(x) \) имеет более низкую степень, чем \( g(x) \).
Целью алгоритма деления многочленов в столбик (уголком) является нахождение частного \( q(x) \) и остатка \( r(x) \) для заданных делимого \( f(x) \) и ненулевого делителя \( g(x) \)
Пример
Разделим один многочлен на другой многочлен (двучлен) столбиком (уголком):
$$ \frac
6. Конец алгоритма.
Таким образом, многочлен \( q(x)=x^2-9x-27 \) — частное деления многочленов, а \( r(x)=-123 \) — остаток от деления многочленов.
Результат деления многочленов можно записать в виде двух равенств:
\( x^3-12x^2-42 = (x-3)(x^2-9x-27)-123 \)
или
$$ \frac
Алгоритм деления «уголком» многочленов от одной переменной
Напомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:
где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:
Если друг на друга делить многочлены, то возникает похожая ситуация.
Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.
Однако в результате деления многочленов многочлен получается далеко не всегда.
Очень важно отметить, что формула
При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.
К описанию этого способа деления многочленов мы сейчас и переходим.
Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.
Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.
пишем под вторым остатком.
Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен.
Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:
Деление многочленов.
Вспомним для начала о рациональных дробях и о выделении целой части из неправильных дробей.
Рациональная дробь называется правильной, если числитель меньше знаменателя, в противном случае – неправильной.
Будем работать только с несократимыми дробями, то есть 



Как происходит процесс выделения целой части из неправильной дроби: мы делим числитель на знаменатель столбиком (уголком) и дробь представляется в виде суммы целой части и дробной части. Дробная часть – это отношение остатка от деления и знаменателя.
Покажем это на примере.
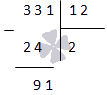
Найти остаток от деления 27 на 4.
Разделим натуральные числа столбиком:
Следовательно,
Выделить целые части из дробей 

Разделим числитель первой дроби на знаменатель уголком:
Делим дальше:
Поэтому, 
Вторая дробь – правильная, следовательно, ее целая часть равна нулю.
Теперь перейдем к отношению многочленов, то есть к дробно рациональной функции (смотрите классификацию элементарных функций).
Дробно рациональная функция называется правильной, если степень числителя меньше степени знаменателя, в противном случае – неправильной.
Деление многочлена на многочлен производится по тому же принципу – столбиком (уголком) и функция представляется в виде суммы «целой части» и дробной части.
Для деления многочлена на линейный двучлен очень удобно использовать схему Горнера.
Рассмотрим примеры деления многочленов.
Разделить многочлен 

Запишем в виде дроби и воспользуемся свойством деления:
Очень часть такие преобразования приходится делать при взятии интегралов.
Выполнить деление многочлена 

Отношение многочленов можно записать в виде дроби 
Следовательно, целая часть равна двум, остаток от деления многочленов есть двучлен 

Найти остаток от деления многочлена 
Запишем дробь
Степень числителя больше степени знаменателя, то есть, дробь неправильная. Выделим «целую часть» дробно рациональной функции, выполнив деление столбиком (уголком).
Продолжаем деление.
Таким образом, остаток от деления многочленов равен 
Иногда бывает достаточно выполнить преобразование дроби, чтобы выявить остаток от деления числителя на знаменатель:
Следовательно, остаток от деления многочлена 


Иногда очень быстро прийти к результату позволяет использование формул сокращенного умножения.
Выполнить деление многочлена 

Запишем отношение в виде дроби:
В числителе находится выражение, представляющее собой куб суммы, поэтому
Вывод: исходный многочлен делится на двучлен без остатка.
Так что выбирайте для себя наиболее удобный вариант решения, но помните – деление многочлена на многочлен столбиком является универсальным способом.