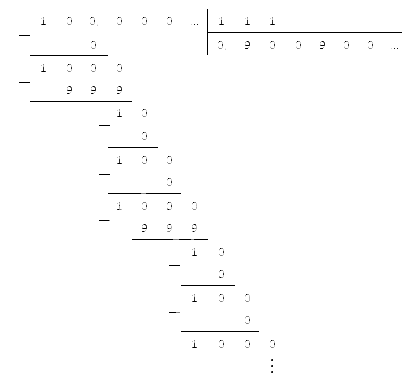
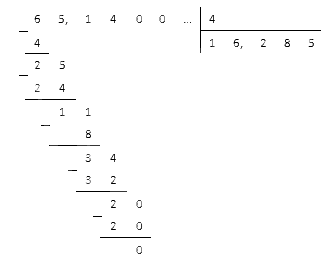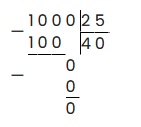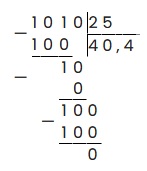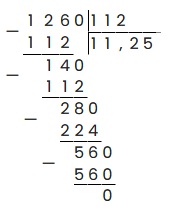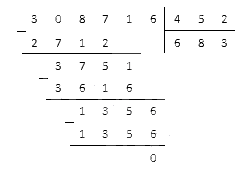Как поделить на нецелое число
Деление десятичных дробей: правила, примеры, решения
Здесь мы возьмем только случаи с положительными дробями. Если же перед дробью стоит минус, то для действия с ней нужно изучить материал о делении рациональных и действительных чисел.
Основы деления десятичных дробей
Все десятичные дроби, как конечные, так и периодические, представляют из себя всего лишь особую форму записи обыкновенных дробей. Следовательно, на них распространяются те же принципы, что и на соответствующие им обыкновенные дроби. Таким образом, весь процесс деления десятичных дробей мы сводим к замене их на обыкновенные с последующим вычислением уже известными нам способами. Возьмем конкретный пример.
Решение
Запишем десятичные дроби в виде обыкновенных. У нас получится:
Решение
Для начала нам нужно перевести периодическую десятичную дробь в обыкновенную.
У нас получился результат, который мы также можем перевести в десятичный вид. Для этого разделим числитель на знаменатель, используя метод столбика:
Если же в примере на деление нам встретились непериодические десятичные дроби, то мы будем действовать немного иначе. Мы не можем их привести к привычным обыкновенным дробям, поэтому при делении приходится предварительно округлять их до определенного разряда. Это действие должно быть выполнено как с делимым, так и с делителем: имеющуюся конечную или периодическую дробь в интересах точности мы тоже будем округлять.
Решение
Первым делом мы округляем обе дроби до сотых. Так мы переходим от бесконечных непериодических дробей к конечным десятичным:
Точность результата будет зависеть от степени округления.
Как разделить натуральное число на десятичную дробь и наоборот
Подход к делению в этом случае практически аналогичен: конечные и периодические дроби заменяем обыкновенными, а бесконечные непериодические округляем. Возьмем для начала пример деления с натуральным числом и десятичной дробью.
Решение
Как разделить десятичную дробь на натуральное число столбиком
Метод деления столбиком хорош не только для натуральных чисел. По аналогии мы можем использовать его и для дробей. Ниже мы укажем последовательность действий, которую нужно для этого осуществить.
Для деления столбиком десятичных дробей на натуральные числа необходимо:
1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).
2. Разделить столбиком десятичную дробь на натуральное число, используя алгоритм. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.
Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться, то ответом будет периодическая дробь.
Возьмем для примера несколько задач и попробуем выполнить эти шаги уже с конкретными числами.
Решение
Полученное число и будет нужным нам результатом деления целой части. Ставим запятую, отделяя ее, и продолжаем:
Мы добрались до нулевого остатка, следовательно, процесс деления завершен.
Деление десятичных чисел
Перед тем как перейти к вопросу, о том, как делить десятичные дроби, вспомним теоретические основы. Итак:
Десятичная дробь — это представление обыкновенной дроби в десятичной форме, где знаменатель равен 10, 100, 1000 и т.д. Другими словами, десятичная дробь — это результат деления числителя на знаменатель. К примеру, ½ = 0,5.
Как делить десятичные дроби?
Деление десятичных дробей сводится к делению обыкновенных дробей. Рассмотрим подробнее основные правила деления десятичных дробей.
Деление десятичной дроби на натуральное число
Напомним, что натуральные числа — это числа, которые мы используем в повседневной жизни, для подсчета (1, 2, 3, 4 и т.д). Алгоритм деления натурального числа на десятичную дробь в столбик, выглядит так:
Чтобы разделить десятичную дробь на натуральное числа используем стандартный алгоритм деления в столбик.
Пример 1: Разделить 100 на 2,5.
Согласно вышеприведенному алгоритму, избавимся от запятой. Таким образом добавим к 100 один 0 и получим 1000 : 25. Решение будет выглядеть так:
Пример 2: Разделить 101 на 2,5.
Аналогично предыдущему примеру, избавимся от запятой. Таким образом получим 1010 : 25, где решение:
Ответ: 101 : 2.5 = 40.4
Пример 3: Разделить 7.5 на 3.
В этом примере, деление осуществляется по стандартному алгоритму деления столбиком. Таким образом:
Как делить десятичную дробь на целое число?
Производим вычисления, по алгоритму деления натурального числа на десятичную дробь, не обращая внимания на знаки (чтобы не запутаться знаки можно не писать):
Из правила следует, что плюс разделить на минус будет минус, таким образом:
Деление двух десятичных дробей
Деление двух десятичных чисел сводится к предыдущему алгоритму, т.е. необходимо избавиться от запятых. В случае, если в делителе, цифр после запятой больше чем в делимом, необходимо в делимое добавить соответствующее количество нулей.
Пример 5: Разделить 12,6 на 1,12.
Т.к. в делителе (1,12) две цифры после запятой, то для избавления от запятых, необходимо в делимом (12,6), добавить ноль, таким образом:
Ответ: 12.6 : 1.12 = 11.25
Деление десятичных дробей на 10, 100, 1000
Правило деления десятичной дроби на 10, 100, 1000 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую влево на столько цифр, сколько нулей в делителе после единицы.
Деление десятичных дробей на 0,001, 0,01, 0,1
Правило деления десятичной дроби на 0,001, 0,01, 0,1 и т.д. состоит в том, что для получения ответа, необходимо в этой дроби перенести запятую вправо на столько цифр, сколько нулей в делителе перед единицей.
Деление десятичных дробей
При делении десятичных дробей вам могут встретиться несколько случаев.
Деление десятичной дроби на натуральное число
Для деления десятичной дроби на натуральное число пользуемся следующими правилами.
Если целая часть делимого меньше делителя, то в частном ставим 0 целых.
Обратите внимание, что целая часть десятичной дроби (у нас это 0) меньше, чем делитель (31). Поэтому в частном сразу ставим 0 в целой части.
Не забываем записывать ответ в пример:
Чтобы разделить десятичную дробь на 10, 100, 1000 и т.д., надо перенести запятую в этой дроби на столько цифр влево, сколько нулей стоит после единицы в делителе.
Деление натурального числа на десятичную дробь
Деление десятичных дробей друг на друга
Делить десятичные дроби друг на друга можно разными способами. Мы опишем один из возможных. По традиции, небольшой план действий:
Наибольшее количество знаков (цифр) после запятой у первой десятичной дроби, поэтому ориентируемся на неё. Чтобы превратить 7,44 в целое число нужно умножить его на 100 (cм. умножение десятичных дробей).
Умножаем каждую из десятичных дробей на 100.
Делим обыкновенные числа в столбик и записываем ответ. Помним, что изначально мы делили десятичные дроби.
Разделить десятичную дробь на 0,1; 0,01; 0,001 и т.д. — то же самое, что умножить её на 10, 100, 1000 и т.д. соответсвенно.
Деление десятичных дробей: правила, примеры
В данной публикации мы рассмотрим, как десятичную дробь можно разделить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления изложенного материала.
Деление десятичной дроби на натуральное число
Делитель – 10, 100, 1000, 10000 и т.д.
Чтобы разделить десятичную дробь на натуральное число 10, 100, 1000, 10000 и т.д., выполняем перенос десятичного разделителя (запятой) влево на столько позиций, сколько нулей содержит делитель.
Пример 1
Объяснение: В числе 10 всего один ноль, значит запятую сдвигаем на одну позицию влево.
Пример 2
Объяснение: В числе 100 два нуля, значит запятую сдвигаем на две позиции.
Примечание: если количество нулей в делителе больше количества цифр в целой части делимого, значит отсчитываем столько позиций, сколько позволяет дробь, затем дописываем оставшееся количество нулей слева, ставим запятую и добавляем ноль в целой части новой десятичной дроби.
Пример 3
62,75 : 1000 = 0,06275
Объяснение: Т.к. в числе 1000 три нуля, отсчитываем две позиции влево, добавляем оставшийся ноль с левой стороны, пишем запятую и затем – ноль в целой части полученной дроби.
Делитель – любое число
Чтобы разделить десятичную дробь на любое натуральное целое число:
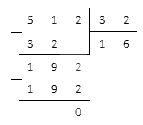
Пример 4: разделим дробь 12,516 на 3.
Пример 5: разделим дробь 3,726 на 15.
Т.к. целая часть исходной дроби меньше делителя, значит целая часть частного равняется 0 (т.е. пишем ноль, ставим запятую и продолжаем выполнять деление).
Деление десятичной дроби на другую десятичную дробь
Чтобы разделить одну десятичную дробь на другую, умножаем обе дроби на такое число (10, 100, 1000 и т.д.), чтобы они стали целыми числами (количество нулей у множителя зависит от наибольшего количества цифр после запятой у той или иной дроби). Затем находим частное.
Примечание: этот же прием можно применять, чтобы разделить десятичную дробь на целое число.
Пример 6: найдем, сколько будет 5,468 делить на 3,2.
У дроби 5,468 три цифры после запятой, а у 3,2 – всего одна. Значит их обе умножаем на 1000, затем находим требуемый результат.
Деление целых чисел: правила, примеры
Данная статья рассказывает о том, как делить без остатка целые числа, то есть нацело. Будут введены термины и обозначения для дальнейшего описания чисел, деление положительных и отрицательных чисел. В итоге произведем проверку вычислений.
Термины и обозначения
При делении целых чисел используются те же термины, что и при описании натуральных чисел.
Делимое – это число, над которым совершают деление.
Делитель – число, на которое делят.
Частное – результат деления.
Деление целых чисел
Между умножением и делением натуральных чисел существует связь. Это связано с тем, что при делении можно найти частное, которое при обратном действии будет считаться множителем. Иначе можно записать, что деление целых чисел служит нахождением одного из целых множителей.
Частное от деления считается целым тогда, когда получается результат без остатка, то есть целое число a должно делиться на число b с целым частным в результате.
Правила деления целых чисел
Можно сделать вывод, что необходимо использовать правила, которые позволяют производить деление целых чисел. Они позволят делить целые и натуральные числа.
Деление целых положительных чисел
Целыми положительными числами называют натуральные числа, поэтому деление целых положительных чисел производится, исходя из правил деления натуральных чисел. Рассмотрим несколько примеров для детального просмотра деления целых положительных чисел.
Решение
Когда имеем большое число, деление лучше всего производить в столбик:
Правило деления целых отрицательных чисел, примеры
Для определения знака числа с необходимо выяснить, какие знаки находятся перед делимым и делителем.
Исходя из смысла деления целых чисел, равенство b · c = a справедливо. Правило умножения целых чисел говорит о том, что частное должно быть положительным. Иначе, b · c будет производиться по правилам целых отрицательных чисел. Частное с от деления целых отрицательных целых чисел является положительным числом.
Рассмотрим несколько примеров деления отрицательных чисел.
Решение
Для решения необходимо разделить числа по модулю. Деление производится столбиком.
Правило деления целых чисел с разными знаками, примеры
Выделим правило деления целых чисел, содержащих разные знаки.
Детально разберем примеры, где необходимо применить правило деления целых чисел с разными знаками.
Решение
Данный пример показывает правильное деление целых чисел с разными знаками. Для этого необходимо применить правило
Деление нуля на целое число
Для углубления в правило рассмотрим некоторые пояснения.
Не делить на нуль
Проверка результата деления целых чисел
Проверку осуществляют умножением. Чтобы произвести проверку деления, нужно полученное частное умножить на делитель, если в результате получается число, равное делимому, тогда результат считается правильным.
Рассмотрим на примере решение с проверкой результата.
Решение