Как поделить положительное число на отрицательное
Урок 37 Бесплатно Деление
В прошлом уроке мы познакомились с умножением.
Сейчас перейдем к делению, узнаем правила деления для чисел с разными знаками, деления отрицательных чисел, проведем параллели между умножением и делением, а также определим, какой может быть знак результата деления в зависимости от знаков делимого и делителя.
Деление отрицательных чисел
Правило: для того, чтобы разделить одно отрицательное число на другое отрицательное число, необходимо разделить модуль первого числа на модуль второго числа.
Это правило очень похоже на правило для умножения. Откуда такая схожесть мы узнаем чуть позже, а пока посмотрим на примеры.
Пример:
Допустим надо разделить -15 на -5
1) Найдем модули от этих чисел:
2) Посчитаем частное этих двух чисел:
Пример:
Разделим -132 на -3
1) Находим модули этих чисел:
2) Посчитаем частное модулей:
Это правило работает для нецелых чисел:
2) Выполняем деление:
И еще несколько примеров уже менее подробно:
Пройти тест и получить оценку можно после входа или регистрации
Деление чисел с разными знаками
Допустим, мы знаем, что на заводе 250 работников, получающих одинаковую зарплату, также мы знаем, что вся сумма денег на выплату зарплат изменилась на -100000 рублей.
На сколько изменилась зарплата каждого конкретного работника?
Необходимо разделить общее изменение на количество работников. Иными словами, необходимо разделить отрицательное число на положительное.
Правило: чтобы разделить отрицательное число на число положительное, нужно поделить модуль первого числа на модуль второго числа и к результату деления приписать минус.
Воспользуемся им для решения задачи:
1) Берем модули чисел:
3) И приписываем к результату минус:
Получаем, что зарплата каждого работника изменилась на -400 рублей, иными словами, уменьшилась на 400 рублей.
Теперь посмотрим, как разделить положительное число на отрицательное.
Правило: чтобы разделить положительное число на число отрицательное, нужно поделить модуль первого числа на модуль второго числа и к результату приписать минус.
Допустим, необходимо разделить 161 на -7:
1) Посчитаем модули:
2) Посчитаем частное:
3) И приписываем к нему минус:
Это и будет ответом.
Заметим, что оба правила достаточно похожи, поэтому можно их обобщить и запомнить общее правило.
Правило: чтобы посчитать частное чисел с разными знаками, необходимо посчитать частное их модулей и приписать к нему минус.
Пройти тест и получить оценку можно после входа или регистрации
Сведение деления к умножению
Вы уже могли заметить, что правила для умножения и деления весьма похожи. Это вполне закономерно.
Как мы уже говорили в уроке про деление дробей, деление можно заменить умножением делимого на число, обратное делителю.
И это верно для отрицательных чисел тоже.
Посмотрим, как это происходит на примерах.
1-й способ: воспользоваться правилом для деления отрицательных чисел:
2-й способ: представить деление как умножение на число, обратное делителю, и воспользоваться правилом для умножения отрицательных чисел:
Как вы можете заметить, результаты вычислений разными подходами совпадают. Более того, совпадают даже последние действия, поэтому можете выбирать любой удобный для вас способ.
Такой же подход работает и для деления чисел с разными знаками.
Пример:
1-й способ: воспользуемся правилом для деления чисел с разными знаками:
2-й способ: заменим деление на умножение и воспользуемся правилом для умножения чисел с разными знаками:
Можно заметить, что результаты совпадают.
Так что можно выбирать любой способ для выполнения деления чисел с разными знаками.
Пройти тест и получить оценку можно после входа или регистрации
Определение знака частного
Если мы хотим определить, какой знак будет у частного, не считая его, тогда нам помогут следующие правила:
Правило: частное двух отрицательных чисел всегда число положительное
Пример:
Частное \(\mathbf<-32>\) и \(\mathbf<-4>\) будет больше нуля.
Правило: частное положительного числа и отрицательного равно нулю
Пример 1:
Частное 45 и \(\mathbf<-5>\) будет меньше нуля.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Мы уже говорили о площади круга и площади квадрата.
Эти знания нам сейчас пригодятся, потому что так мы можем найти математическую ошибку в одном литературном произведении, а именно, в романе Джека Лондона «Маленькая хозяйка большого дома».
«Посреди поля возвышался стальной шест, врытый глубоко в землю. С верхушки шеста к краю поля тянулся трос, прикреплённый к трактору. Механики нажали рычаг, и мотор заработал.
Машина сама двинулась вперёд, описывая окружность вокруг шеста, служившего его центром.
– Чтобы окончательно усовершенствовать машину, Грэхем, вам остаётся превратить окружность, которую она описывает, в квадрат.
– Да, на квадратном поле пропадает при такой системе очень много земли.
Грэхем произвёл некоторые вычисления, затем заметил:
– Теряем примерно три акра из каждых десяти.
И сейчас мы проверим, прав ли был Грэхем.
Посчитаем площадь квадрата: возводим длину сторон х в квадрат.
Так что площадь квадрата- \(\mathbf
Теперь посчитаем площадь круга: \(\mathbf<\pi(\frac
Теперь мы можем вычесть из площади квадрата площадь круга и понять, какая часть площади не используется.
Как мы видим, не используется 0.22 земли, что явно меньше 0.3, о которых говорится в тексте.
Возможно, так автор хотел изобразить математическое невежество героев, или же он просто не уделил внимание таким подробностям.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если « a » и « b » положительные числа, то разделить число « a » на число « b », значит найти такое число « с », которое при умножении на « b » даёт число « a ».
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число « −15 » на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число « −15 ». Таким числом будет « −3 », так как
Примеры деления рациональных чисел.
Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками— число отрицательное (примеры 3, 4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
Примеры деления чисел с одинаковыми знаками:
Чтобы разделить два числа с разными знаками, надо:
Примеры деления чисел с разными знаками:
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби
Можно обратить внимание, что в числителе два знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
Частное от деления нуля на число, отличное от нуля, равно нулю.
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.
Пример нахождения неизвестного.
Знак «минус» в дробях
Разделим число « −5 » на « 6 » и число « 5 » на « −6 ».
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
Деление чисел с разными знаками: правило и примеры
В этой статье мы рассмотрим деление положительных чисел на отрицательные и наоборот. Дадим подробный разбор правила деления чисел с разными знаками, а также приведем примеры.
Правило деления чисел с разными знаками
Правило для целых чисел с разными знаками, полученное в статье о делении целых чисел, справедливо также для рациональных и действительных чисел. Приведем более общую формулировку этого правила.
Правило деления чисел с разными знаками
При делении положительного числа на отрицательное и наоборот нужно модуль делимого разделить на модуль делителя, а результат записать со знаком минус.
В буквенном виде это выглядит так:
Результатом деления чисел с разными знаками всегда является отрицательное число. Рассмотренное правило, по сути, сводит деление чисел с разными знаками к делению положительных чисел, так как модули делимого и делителя являются положительными.
Еще одна эквивалентная математическая формулировка данного правила имеет вид:
Рассмотрим теперь, как применять описанную выше теорию на практике.
Как делить числа с разными знаками? Примеры
Ниже мы рассмотрим несколько характерных примеров.
Пример 1. Как делить числа с разными знаками?
Сначала запишем модули делимого и делителя:
Теперь разделим модули:
Допишем перед результатом знак минус и получим ответ:
Теперь проведем умножение:
Это и есть окончательный ответ.
Если мы делим дробные числа с рациональными знаками, делимое и делитель нужно представить в виде обыкновенных дробей.
Пример 3. Как делить числа с разными знаками?
Делитель также представим в виде обыкновенной дроби:
Теперь делим обыкновенные дроби, выполняем сокращения и получаем результат:
В заключение рассмотрим случай, когда делимое и делитель являются иррациональными числами и записываются в виде корней, логарифмов, степеней и т.д.
В такой ситуации частное записывается в виде числового выражения, которое по возможности упрощается. При необходимости вычисляется его приближенное значение с необходимой точностью.
Пример 4. Как делить числа с разными знаками?
По правилу деления чисел с разными знаками, запишем равенство:
Избавимся от иррациональности в знаменателе и получим окончательный ответ:
Деление чисел с разными знаками, правило, примеры.
В данной статье дается подробный обзор деления чисел с разными знаками. Сначала приведено правило деления чисел с разными знаками. Ниже разобраны примеры деления положительных чисел на отрицательные и отрицательных чисел на положительные.
Навигация по странице.
Правило деления чисел с разными знаками
В статье деление целых чисел было получено правило деления целых чисел с разными знаками. Его можно распространить и на рациональные числа, и на действительные числа, повторив все рассуждения из указанной статьи.
Итак, правило деления чисел с разными знаками имеет следующую формулировку: чтобы разделить положительное число на отрицательное или отрицательное число на положительное, надо модуль делимого разделить на модуль делителя, и перед полученным числом поставить знак минус.
Из озвученного правила понятно, что результатом деления чисел с разными знаками является отрицательное число. Действительно, так как модуль делимого и модуль делителя есть положительнее числа, то их частное есть положительное число, а знак минус делает это число отрицательным.
Отметим, что рассмотренное правило сводит деление чисел с разными знаками к делению положительных чисел.
Это правило можно использовать, когда есть возможность выходить за пределы множества целых чисел (так как далеко не каждое целое число имеет обратное). Иными словами, оно применимо на множестве рациональных, а также на множестве действительных чисел.
Понятно, это правило деления чисел с разными знаками позволяет от деления перейти к умножению.
Это же правило используется при делении отрицательных чисел.
Осталось рассмотреть, как данное правило деления чисел с разными знаками применяется при решении примеров.
Примеры деления чисел с разными знаками
Рассмотрим решения нескольких характерных примеров деления чисел с разными знаками, чтобы усвоить принцип применения правил из предыдущего пункта.

При делении дробных рациональных чисел с разными знаками их обычно делимое и делитель представляют в виде обыкновенных дробей. Это связано с тем, что с числами в другой записи (например, в десятичной) не всегда удобно выполнять деление.

В заключение стоит отметить, что если делимое и (или) делитель является иррациональным числом, записанным как корень, степень, логарифм и т.п., то частное часто записывается в виде числового выражения. Выражение по возможности упрощается, а его значение вычисляется приближенно с требуемой точностью только при необходимости.
Разделите положительное число 5/7 на отрицательное число 

Смотрите также материал статьи деление действительных чисел.
Остаток от деления отрицательных чисел
В этой статье я расскажу о том, как правильно находить остаток от деления отрицательных чисел. Этой теме, к сожалению, уделяется очень мало внимания в школе, хотя для понимания учеником базовых основ математики она чрезвычайно важна. Именно поэтому, как репетитор по математике, на своих занятиях я разбираю это материал с учениками во всех подробностях. Это значительно упрощает дальнейшую подготовку к ЕГЭ, ОГЭ, вступительным экзаменам и олимпиадам по математике.
Итак, приступим. Чтобы разделить друг на друга два целых числа с остатком, нужно воспользоваться следующей теоремой:
Для любых целых чисел 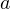 и и 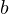 , причём , причём 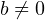 , найдётся единственная пара целых чисел , найдётся единственная пара целых чисел 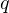 и и  , таких что , таких что 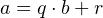 , где , где 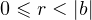 . . |
Здесь 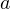
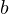
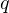


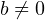
Звучит довольно сложно, но на самом деле в этой теореме нет ничего сложного. Чтобы во всём разобраться, перейдём к примерам.
Примеры нахождения остатка от деления отрицательных чисел
Пример 1. Деление с остатком положительного целого числа на положительное целое число.
Допустим, что требуется разделить с остатком 27 на 4. Вопрос состоит в том, сколько раз число 4 содержится в числе 27? Но мы знаем, что нет такого целого числа, на которое можно умножить 4, чтобы получить 27. Поэтому вопрос нужно переформулировать. На какое число нужно умножить 4, чтобы получить число, максимально близкое к 27, но не превзойти его? Очевидно, что это число 6. Если 4 умножить на 6, то получится 24. До исходного делимого 27 не хватает 3. Следовательно, остаток от деления 27 на 4 составляет 3:
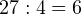
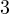
Пример 2. Деление с остатком отрицательного целого числа на положительное целое число.
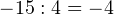
Пример 3. Деление положительного целого числа на отрицательное целое число.
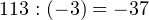
Пример 4. Деление с остатком отрицательного целого числа на отрицательное целое число.
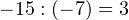
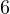
Проверьте, насколько хорошо вы поняли этот урок. Найдите самостоятельно остаток от деления отрицательных чисел:
Свои ответы пишите в комментариях, я их проверю.









