Как подготовиться к зно по математике

ЗНО по математике: особенности теста 2022 года

Тест внешнего независимого оценивания по математике в 2022 году состоит из заданий четырех форм: заданий с выбором одного правильного ответа, заданий на установление соответствия, заданий открытой формы с кратким ответом (структурированное и неструктурированное), а также заданий открытой формы с развернутым ответом.

Общее количество заданий теста по математике – 32, на выполнение которых участникам будет отведено 180 минут.

Результат выполнения заданий №1–26 будет засчитан как государственная итоговая аттестация по математике для тех учеников, студентов учебных заведений, которые в 2022 году завершают получение полного общего среднего образования, и изучали математику на уровне стандарта.

Результат выполнения заданий всего теста будет засчитан как государственная итоговая аттестация по математике для тех учеников, студентов учебных заведений, которые в 2022 году завершают получение полного общего среднего образования, и изучали математику на профильном уровне, а также будет использоваться во время приема в учреждения высшего образования Украины.

Максимальное количество тестовых баллов, которое может получить участник ЗНО, правильно выполнив все задания №1-26, которые будут засчитываться как государственная итоговая аттестация на уровне стандарта, равняется 40 баллам.

Максимальное количество тестовых баллов, которое можно набрать, правильно выполнив все задания теста – 62 балла.

ФОРМЫ ТЕСТОВЫХ ЗАДАНИЙ

Задание с выбором одного правильного ответа (№1–16) — задание состоит из основы и пяти вариантов ответа, из которых только один правильный. Задание считается выполненным, если участник внешнего независимого оценивания выбрал и обозначил ответ в бланке ответов А.

Задание с выбором одного правильного ответа оценивается в 0 или 1 балл: 1 балл, если указан правильный ответ; 0 баллов, если указан неправильный ответ, или указано более одного ответа, или ответ на задание не предоставлен.

Задание на установление соответствия («логические пары») (№17–20) — задание состоит из основы и двух колонок информации, обозначенных цифрами (слева) и буквами (справа). Выполнение задания предполагает установление соответствия (образования «логических пар») между информацией, обозначенной цифрами и буквами. Задание считается выполненным, если участник внешнего независимого оценивания сделал отметки на пересечениях строк (цифры от 1 до 3) и колонок (буквы от А до Д) в таблице бланка ответов А.

Задание на установление соответствия (логические пары) оценивается в 0, 1, 2 или 3 балла: 1 балл – за каждое правильно установленное соответствие (логическую пару); 0 баллов за любую «логическую пару», если сделано более одной отметки в строке и/или колонке; 0 баллов за задание, если не указано ни одного правильного соответствия (логической пары), или ответ на задание не предоставлен.

Структурированное задание открытой формы с кратким ответом (№21–24) — задание состоит из основы и двух частей и предусматривает решение задачи. Задача считается выполненной, если участник внешнего независимого оценивания, осуществив соответствующие числовые расчеты, записал, соблюдая требования и правила, ответы на каждую из частей задания в бланке ответов А.

Структурированное задание оценивается в 0, 1 или 2 балла: 1 балл за каждый правильно указанный ответ; 0 баллов, если указаны оба неправильных ответа, или ответ на задание не предоставлен;

Неструктурированное задание открытой формы с кратким ответом (№25–29) — задание состоит из основы и предусматривает решение задачи. Задача считается выполненной, если участник внешнего независимого оценивания, совершив соответствующие числовые расчеты, записал, соблюдая требования и правила, конечный ответ в бланке ответов А.

Неструктурированное задание оценивается в 0 или 2 балла: 2 балла, если указан правильный ответ; 0 баллов, если указан неправильный ответ, или ответ на задание не предоставлен.

Задание открытой формы с развернутым ответом (№30–32) — задание состоит из основы и предусматривает решение задачи. Задача считается выполненной, если участник внешнего независимого оценивания в бланке ответов Б привел все этапы решения и обосновал их, сделал ссылку на математические факты, из которых следует то или иное утверждение, проиллюстрировал решение задачи рисунками, графиками и т. д.

Задания открытой формы с развернутым ответом № 30, 32 оцениваются в 0, 1, 2, 3, 4, 5 или 6 баллов; Задание №31 оценивается в 0, 1, 2, 3 или 4 балла.

Задания с развернутым ответом оцениваются в соответствии с утвержденными критериями оценивания.

Решения заданий в черновике не проверяются и не учитываются.

Советуем участникам тестирования по математике ознакомиться со следующими материалами:

Источник

Как подготовиться к ЗНО по математике

Сдаем математику без страха: как подготовиться к ЗНО комплексно.

Точные науки считаются наиболее сложными, так как требуют полного погружения в предмет и строгого знания формул и основных постулатов. Поэтому подготовку к ЗНО по математике следует начинать заблаговременно: желательно, чтобы будущий выпускник приступил к ней еще в начале учебного года. Тогда на оценивании его непременно ждет успех.

Советы подготовки к ЗНО по математике.

Для того, чтобы подготовка прошла максимально эффективно, ученику следуют составить список шагов и следовать ему.

1. Посещение ВУЗов.

Если школьник хочет узнать как подготовиться к ЗНО по математике, то ему в первую очередь стоить посетить те заведения, куда он хочет поступать. Везде требуются разные баллы по этой дисциплине. Также ему следует выяснить, будет ли этот предмет на курсе и какие в основном разделы проходят студенты, чтобы подтянуть именно эти области.

2. Практика.

Для тех, кто не знает, как лучше самостоятельно подготовиться к ЗНО по математике опытные педагоги рекомендуют как можно больше практиковаться:

3. Наглядный материал.

Учителя или студенты знают, как быстро подготовиться к ЗНО по математике – скачивать и распечатывать готовые учебники. Желательно, чтобы в них были не только теоретические разделы, но и практика в виде контрольных срезов или тестирования. Не обязательно покупать эту литературу – обратитесь к педагогу или поищите книги в интернете в свободном доступе.

4. Репетитор.

Если ученик имеет большие пробелы в математике и не в состоянии самостоятельно нагнать программу за несколько лет, лучше не экономить средства и потратить их на хорошего специалиста. Индивидуальное обучение поможет очень быстро и эффективно восстановить материал:

5. Видео-уроки.

Сегодня в интернете можно найти практически любые уроки по математике. Существует масса групп и сообществ, посвященных именно подготовке к ЗНО по данной дисциплине, где дети могут не только получать материал, но и задавать интересующие их вопросы.

Не стоит забывать и о обучающих фильмах – зачастую они длятся намного дольше, чем видео-уроки, но зато и информации в них в разы больше.

6. Курсы подготовки к ЗНО по математике онлайн.

Курсы помогут наверстать знания даже тогда, когда ученик совсем не разбирается в математике и рискует «завалить» экзамены:

Еще один неоспоримый плюс интерактивных курсов – даже самые застенчивые дети не будут испытывать стресс, а спокойно сосредоточатся на предмете.

7. Четкий график.

Информацию нужно получать дозированно в определенное время, чтобы не перенапрячься. Поэтому ученику следует составить расписание, отводя время не только на занятия, но и на отдых.

Источник

Как подготовиться к зно по математике

Но это дорого и занятия
проходят в группах,
что весело,
но не супер эффективно.

Найти репетитора?

Но это очень дорого,
если качественно
и некачественно, если дешево.

Пройти онлайн курсы на уважаемом ресурсе?

Но, где найти этот ресурс?
И что делать, если там только
пару десятков видео-уроков
на избранные темы и совсем немного заданий для самоподготовки?

К счастью, Вы попали на сайт
math.ua

и я расскажу Вам о том,
как он устроен и что нужно делать.

Но, для начала я расскажу, как раньше работали репетиторы, когда между школой и вступительными экзаменами в ВУЗы была бездонная пропасть.

На полке в шкафу стояли все учебники с 5 по 11й класс, вечный Сканави и еще парочка сборников задач для абитуриентов. Преподаватель на первом занятии определял уровень подготовки школьника, его способность учиться, смотрел на календарь и составлял у себя в голове план по которому будет двигаться со своим учеником.

Каждое занятие проходило так: тема урока, краткий теоретический материал с ключевыми формулами, несколько примеров разобранных учителем и десяток примеров такого же типа, которые делал ученик. И каждый раз приходилось открывать шкаф, брать определенную книгу и выбирать из нее задачи: 5, 12, 34, 56, 78. И на домашнее задание: 7, 18, 39, 72… Так происходило, потому что Сканави предназначен не для учебы, а для оттачивания навыков приобретенных в школе и задачи разных типов в нем перемешаны. В школьных учебниках они идеально упорядочены, но нет возможности пройти все 11 книг за один год.

Какой должна быть подготовка к ЗНО по математике?

Одни говорят, что последние годы уровень ЗНО по математике упал до нуля, другие говорят, что задачи наоборот стали гораздо сложнее, чем раньше.
Я не хочу вступать в полемику по этому вопросу и навязывать личное мнение о сложности задач, а лишь приведу немного статистики:
Каждый год 1-го сентября в КПИ проводится контрольный срез знаний по школьной математике. Тест этот составлен задолго до появления ЗНО и содержит 8 задач средней сложности ( на 1,5 часа). Каждая задача имеет свой вес, а итоговая оценка выставляется в баллах от 0 до 5.
На специальности (инженерной), где я преподавал с 2009 по 2018й не было студентов у которых ЗНО математика была ниже 165 баллов. Однако, средний балл теста по группе в разное время был таким: 1,6; 1,42; 0,84; 0,96; 1,21 и т.д. Обратите внимание, что это даже не оценка «неудовлетворительно».
Во время учебы четко прослеживалась корреляция между результатом входного контроля и успехами в семестре. А также выяснилось, что при баллах ниже 180, невозможно нормально учиться в ВУЗе.
Вот и ответ на вопрос о том, какой должна быть подготовка: если вы будете готовиться ровно к тем задачам, которые будут на ЗНО, то не сможете нормально учиться в университете.
Поэтому на сайте math.ua предлагается полноценный курс школьной алгебры, геометрии, комбинаторики, который позволит успешно учиться в ВУЗе, а высокие баллы будут лишь следствием правильной подготовки к ЗНО по математике.

Даже у хорошего учителя есть существенное ограничение: он не может одновременно обучить большое количество людей.

Тогда я решил создать сайт, который бы работал, как репетитор. Я продумал последовательность из 282 мини-уроков, которые покрывают все темы от сложения в столбик до задач с параметрами. Взял 20 задачников со своей книжной полки и стал снимать видео к каждому уроку и подбирать соответствующие задачи.

Конечно же, преподаватель следит за текущими успехами своего ученика и корректирует программу в зависимости от способностей конкретного человека.

Этому мы научим со временем наш math.ua.

Сегодня с материалом сайта можно работать так:

Если вы готовитесь поступать на специальность, которая требует высокого уровня знаний по математике, то для подготовки нужно проработать последовательно все уроки из разделов Алгебра, геометрия, начала анализа и комбинаторика с вероятностью (сверху вниз и слева направо). По сути, это та программа подготовки, которая была до появления ЗНО.

Если вам нужно просто сдать благополучно ЗНО и не более того, вот вам список обязательных уроков (в скобках номера уроков, нумерация слева направо сверху вниз):

Если вы перерешали все тесты в интернете и хотите еще. То есть раздел математический марафон, который проводится с 2018 года. Там в каждом шаге есть условия задач, которые никого не оставят равнодушным, и видео с разбором каждого Шага.

Источник

Шлях до математики: кроки успіху

Пошук матеріалів

Select language

Оновлення

Підготовка до ЗНО

Збірка завдань ЗНО за темами

Зміст

Алгебра і початки аналізу

I. Числа і вирази

II. Рівняння, нерівності та їхні системи

III. Функції

IV. Елементи комбінаторики, початки теорії ймовірностей та елементи статистики

Геометрія

V. Планіметрія

VI. Стереометрія

37 коментарів:

Величезне дякую за збірку ЗНО по темах! Ви виконали величезну роботу. Не знаю, щоб я без не її робила) Я правда дуже вдячна)

Суперовий матеріал для підготовки до ЗНО! Вдячний за корисну публікацію і вільний доступ.

Отличный материал! Большое спасибо.

Дуже дякую за матеріали, на це все так часу не вистачало. Ви дуже допомогли.

Велике Вам дякую за вашу величезну роботу! Успіхів Вам та натхнення для нових звершень!

Велике вам дякую! Дуже допомагають ваші роботи, усього вам найкращого!

Спасибо вам огромное) Да поможет Бог нам сдать эти экзамены)

Спасибо большое, очень полезный сайт))

Дуже, дуже дякую за таку грунтовну систематизацію!

Дуже круто!Бажаю автору успіху, наснаги та реалізації подальших, не менш чудових, проєктів. Чекаємо!

Дякую Вам за таку величезну роботу.

просто найкращий сайт для підготовки до ЗНО!) все чітко і зрозуміло) ДЯКУЮ!!))

Велика подяка за Вашу роботу. 🙂

Вау, нереальна робота

Величезне дякую за так чудово систематизовані завдання ЗНО та ще й зрозумілий розв’язок до кожного з них!

Источник

Краткий конспект подготовки к ЗНО по математике №1 «Основы арифметических знаний.»

Подготовка к ВНО. Математика.

Конспект 1. Основы арифметических знаний.

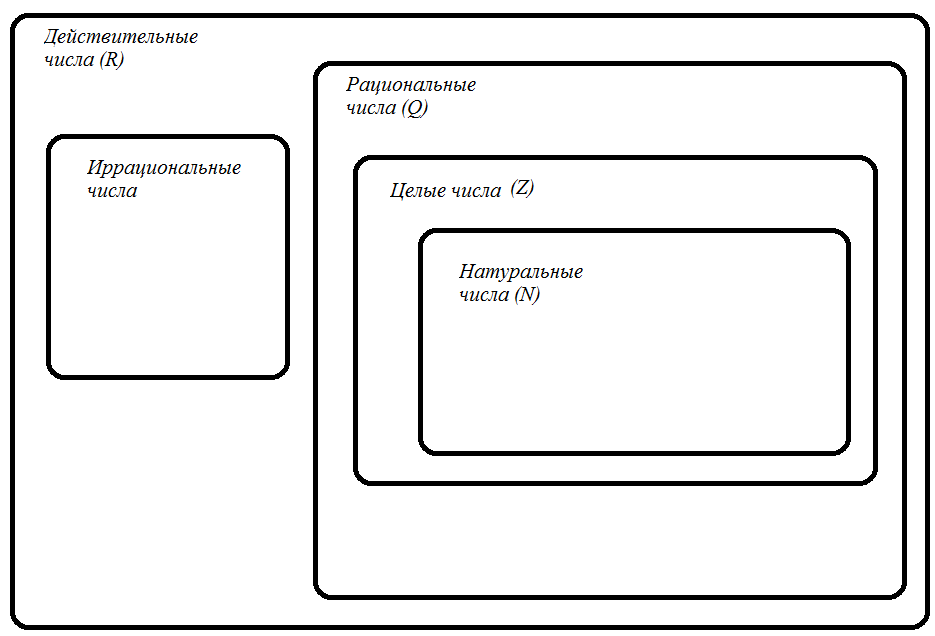
Числовые множества

Все числа, которые используются в математике, принадлежат определённым числовым множествам.

Натуральные числа (N) – это числа, используемые при счёте. Наименьшим числом является 1. Пример: 1, 2, 3, 100 и т. д.

Иррациональные числа – числа, в записи которых присутствует бесконечная непериодическая дробь. Пример: .

Действительные числа (R) – множество, образованное двумя подмножествами – рациональных и иррациональных чисел.

Для того, чтобы сразу определить, на какие числа делится заданное число, в математике используют признаки делимости. Самыми популярными являются следующие признаки делимости.

Число делится на 3, если сумма цифр числа делится на 3. Пример : 22143 делится на 3, так как сумма его цифр равна 2+2+1+4+3 = 12, что делится на 3.

Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Пример: 61348 делится на 4, так как число 48 делится на 4.

Число делится на 9, если сумма цифр числа делится на 9. Пример : 72243 делится на 3, так как сумма его цифр равна 7+2+2+4+3 = 18, что делится на 9.

Работа с дробями

.
Сложение и вычитание дробей выполняется по такому правилу: в случае сложения/вычитания дробей с одинаковыми знаменателями, выполнить сложение/вычитание числителей, а знаменатель оставить прежним. Если складываются две дроби с разными знаменателями, необходимо привести их к общему знаменателю, а потом выполнить действие дробей с одинаковыми знаменателями.
Пример : .
Умножение дробей выполняется по такому правилу: числители и знаменатели дробей попарно перемножаются.
Пример : .
Деление дробей выполняется по такому правилу: дробь-делитель необходимо «перевернуть», затем выполнить умножение.
Пример : .

Online-тест подготовки к ЗНО по математике №1 «Основы арифметических знаний»

Источник