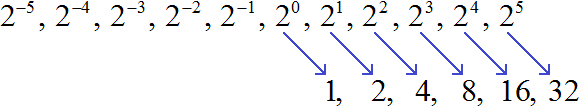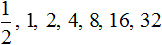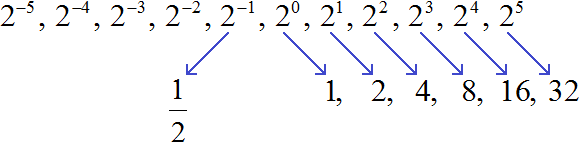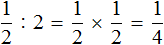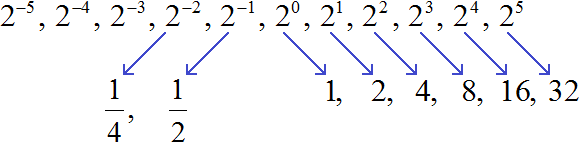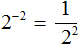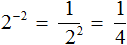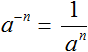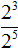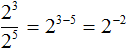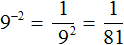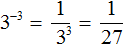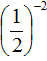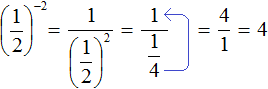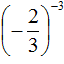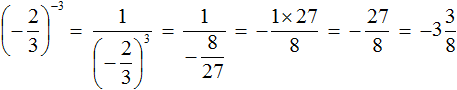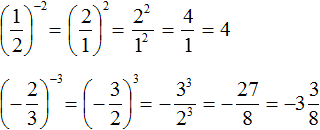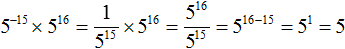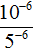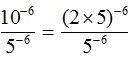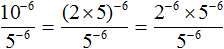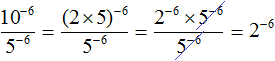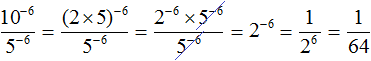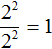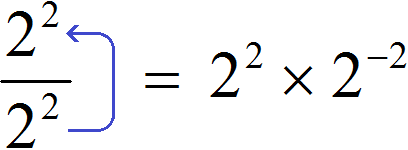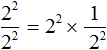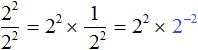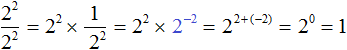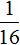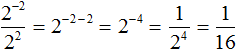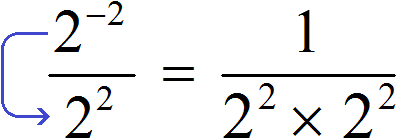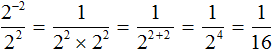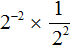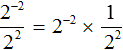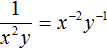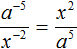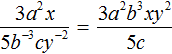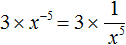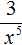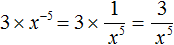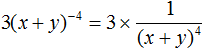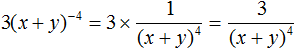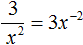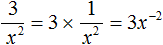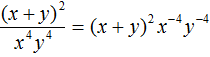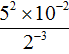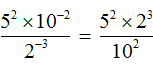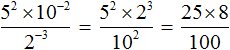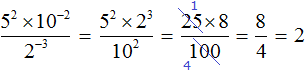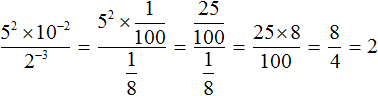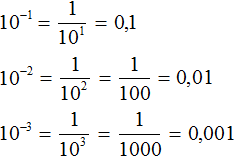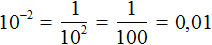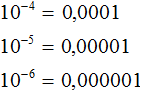Как поднять знаменатель в числитель

Степень с целым показателем

Степень с целым показателем — это степень, показателем которой является любое целое число.

В прошлом уроке мы изучили степень с натуральным показателем. Этот вид степени тоже является степенью с целым показателем, поскольку натуральные числа относятся к целым числам.

Также, мы рассмотрели степень, показателем которой является 0. Этот вид степени тоже является степенью с целым показателем, поскольку 0 относится к целым числам.

Рассмотрим ещё один вид степени с целым показателем, а именно показателем которой является целое отрицательное число. Выглядят эти степени так:

В дальнейшем любую степень с натуральным, нулевым или целым отрицательным показателем, мы будем называть степенью с целым показателем.

Правило вычисления

Рассмотрим следующую последовательность степеней:

Продолжим эту последовательность в сторону степеней с целыми отрицательными показателями:

Теперь попробуем вычислить эти степени. Степени с натуральными показателями и степень, показателем которой является 0, вычисляются легко:

А как вычислить степени с отрицательными показателями? Для начала немного отойдём от темы и затронем несколько закономерностей.

В отрицательную степень число возводится немного иначе. Следует понимать, что если при возведении в положительную степень число увеличивается, то при возведении в отрицательную степень это число наоборот уменьшается.

Например, возьмём число 2. Начиная с нуля будем последовательно увеличивать его показатель:

Вычислим эти степени:

Получили последовательность чисел, в которой каждое число меньше следующего числа в 2 раза. Тогда логично предположить, что число, располагающееся до единицы, будет в два раза меньше единицы. Его можно получить, если 1 разделить на 2

Вернёмся к нашей исходной последовательности, где мы вычисляли степени. Получается, что степень 2 −1 мы вычислили. Она равна рациональному числу

Предыдущее за числом должно быть в два раза меньше, чем . Чтобы его получить разделим на 2

Получили . Это значение степени 2 −2

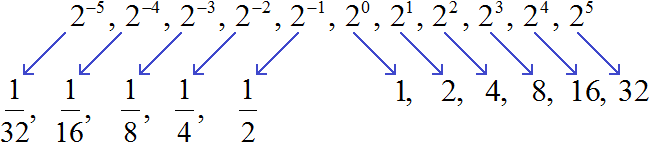
Продолжая деление на 2 можно получить значения остальных степеней с целыми отрицательными показателями:

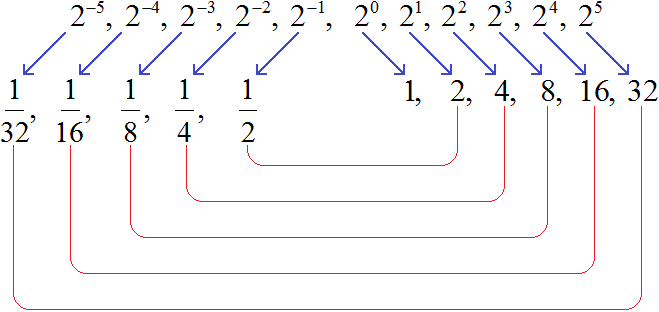
Заметим, что в данной последовательности значения степеней с отрицательными показателями являются обратными числами к значениям степеней с натуральными показателями:

Можно сделать вывод, что для вычисления степени с отрицательным показателем, нужно записать дробь, в числителе которой единица, а в знаменателе та же самая степень, но с противоположным показателем. Покажем это на примере степени 2 −2

Вычислим степень, находящуюся в знаменателе:

Таким образом, чтобы вычислить степень вида a −n можно воспользоваться следующим правилом:

Воспользуемся правилом деления степеней с одинаковыми основаниями:

Получили рациональное число 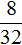. Сократим его на 8. Тогда получим

Пример 2. Найти значение выражения 9 −2

Воспользуемся правилом вычисления степени с целым отрицательным показателем:

Пример 3. Найти значение выражения 3 −3

Действительно, если a будет равным нулю, то в знаменателе получим 0, а на нуль делить нельзя.

Пример 4. Найти значение выражения

Пример 5. Найти значение выражения

При возведении обыкновенных дробей в отрицательную степень, можно пользоваться формулой 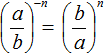. Решим предыдущие два примера с помощью этой формулы:

Желательно уметь возводить обыкновенную дробь в отрицательную степень как с помощью формулы, так и без неё.

Тождественные преобразования

Все тождественные преобразования, которые мы рассматривали при изучении степени с натуральным показателем, сохраняются и для степеней с целыми отрицательными показателями.

Например, чтобы представить выражение 2 −1 × 2 −3 в виде степени, можно воспользоваться основным свойством степени:

2 −1 × 2 −3 = 2 −1 + (−3) = 2 −4

Пример 2. Найти значение выражения 5 −15 × 5 16

Воспользуемся основным свойством степени:

5 −15 × 5 16 = 5 −15 + 16 = 5 1 = 5

Видим, что первый вариант решения намного проще и удобнее.

Пример 3. Найти значение выражения (10 −4 ) −1

Воспользуемся правилом возведения степени в степень:

(10 −4 ) −1 = 10 −4 × (−1) = 10 4 = 10000

Пример 4. Найти значение выражения

В числителе применим правило возведения в степень произведения:

Сократим получившуюся дробь на 5 −6

Вычислим степень 2 −6

Поднятие степени из знаменателя в числитель и наоборот

Если знаменатель дробного выражения содержит степень, то данную степень можно поднять в числитель, изменив знак показателя этой степени на противоположный. Значение выражения при этом не меняется. Данное преобразование иногда используется при упрощении выражений.

Рассмотрим следующее равенство:

Попробуем поднять степень 2 2 из знаменателя в числитель, изменив знак показателя этой степени на противоположный. При этом, поднятую степень и ту степень, которая располагалась в числителе, соединим знаком умножения:

2 2 × 2 −2 = 2 2 + (−2) = 2 0 = 1

Получился тот же результат, что и раньше. Значит значение выражения не изменилось. Как это работает?

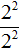
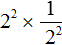
Теперь представим выражение в виде произведения . То есть заменим деление умножением. Напомним, что при замене деления умножением, делимое умножают на число, обратное делителю. А обратное делителю число в данном случае это дробь

Теперь воспользуемся правилом . В произведении заменим дробь на тождественно равное ей выражение 2 −2

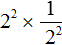
Далее, как и раньше применяем основное свойство степени:

Получился тот же результат 1.

Таким же образом можно опустить степень из числителя в знаменатель, изменив знак показателя этой степени на противоположный.

Рассмотрим выражение 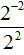. Чтобы найти его значение, воспользуемся правилом деления степеней с одинаковыми основаниями. В результате получим

Теперь попробуем решить этот пример, опустив степень 2 −2 из числителя в знаменатель, изменив знак показателя этой степени на противоположный. При этом, опущенную степень 2 −2 и ту степень, которая располагалась в знаменателе, соединим знаком умножения. А в числителе останется единица:

Дальнейшее вычисление не составит особого труда:

Как и в прошлом примере выражение 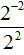представимо в виде произведения

Этим и объясняется появление единицы в числителе, после того как степень 2 −2 была опущена в знаменатель.

Пример 2. Поднять степени из знаменателя дроби 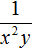в числитель

Пример 3. Поднять степени из знаменателя дроби 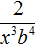в числитель

Пример 4. Поднять степень из знаменателя дроби 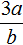в числитель

Пример 5. Опустить степень из числителя дроби 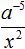в знаменатель

Пример 6. Степень из числителя дроби опустить в знаменатель, а степень из знаменателя поднять в числитель

Представлять дробь в виде произведения вовсе не обязательно. Если пропустить эту запись, то данный пример можно решить короче:

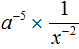
Пример 7. В дроби 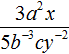перенести из знаменателя в числитель только те степени, которые имеют отрицательные показатели:

Пример 8. Представить произведение 3x −5 в виде дроби, не содержащей степени с отрицательным показателем.

Перепишем произведение 3x −5 с помощью знака умножения:

Сомножитель 3 оставим без изменений, а сомножитель x −5 заменим на тождественно равную ему дробь

Теперь согласно правилу умножения целого числа на дробь, умножим множитель 3 на числитель дроби 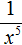. В результате образуется дробь

Пример 9. Представить произведение 3(x + y) −4 в виде дроби, не содержащей степени с отрицательным показателем.

Теперь умножим множитель 3 на числитель дроби 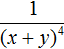. В результате образуется дробь

Пример 10. Представить дробь 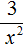в виде произведения.

Чтобы решить этот пример, достаточно поднять степень x 2 в числитель, изменив знак показателя этой степени на противоположный:

Пример 11. Представить дробь 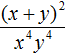в виде произведения.

Пример 12. Найти значение выражения

Поднимем степень 2 −3 из знаменателя в числитель, а степень 10 −2 из числителя опустим в знаменатель:

Вычислим значения степеней, содержащихся в числителе и в знаменателе:

А если бы мы не подняли степень 2 −3 в числитель, и степень 10 −2 не опустили в знаменатель, а стали вычислять каждую степень по отдельности, то получили бы не очень компактное решение:

Возведение числа 10 в целую отрицательную степень

Число 10 в отрицательную степень возводится таким же образом, как и другие числа. Например:

Чтобы возвести число 10 в отрицательную степень, нужно перед единицей записать количество нулей, равное модулю показателя исходной степени.

При этом после первого нуля следует поставить запятую. Примеры:

Представление чисел 0,1, 0,01, 0,001 в виде степени с основанием 10

Чтобы представить числа 0,1, 0,01, 0,001 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать отрицательный показатель, модуль которого равен количеству нулей исходного числа.

Пример 2. Представить число 0,01 в виде степени с основанием 10.

Пример 3. Представить число 0,001 в виде степени с основанием 10.

Пример 4. Представить число 0,0001 в виде степени с основанием 10.

Пример 5. Представить число 0,00001 в виде степени с основанием 10.

Стандартный вид числа

Запишем число 2 000 000 в виде произведения числа 2 и 1 000 000

Сомножитель 1 000 000 можно заменить на степень 10 6

Такой вид записи называют стандартным видом числа. Стандартный вид числа позволяет записывать в компактном виде как большие, так и маленькие числа.

Десятичную дробь 0,001 можно заменить на степень с 10 −3

Значит, число 0,005 в стандартном виде будет выглядеть как 5 × 10 −3

2 × 10 6 = 2 × 1 000 000 = 2 000 000

То есть записывая число в стандартном виде нужно записывать его так, чтобы сохранить его изначальное значение.

Например, представим число 12 в стандартном виде. Для начала проверим становится ли верным неравенство 1 ≤ a при подстановке числа 12 вместо а

Неравенство верным не становится. Чтобы сделать неравенство верным, приведём число 12 к виду, при котором оно удовлетворяло бы данному неравенству. Для этого передвинем в числе 12 запятую влево на одну цифру:

Число 12 обратилось в число 1,2. Это число будет удовлетворять неравенству 1 ≤ a

Значит, чтобы записать число 12 в стандартном виде, нужно представить его в виде произведения 1,2 × 10¹

Пример 2. Записать число 0,5 в стандартном виде.

Пример 3. Записать число 652 000 в стандартном виде.

652 000 = 6,52000 × 10 5

Нули в конце десятичной дроби 6,52000 можно отбросить. Тогда получим более компактную запись:

652 000 = 6,52 × 10 5

Пример 5. Записать число 1 024 000 в стандартном виде.

1 024 000 = 1,024000 × 10 6

Нули в конце десятичной дроби 1,024000 можно отбросить:

1 024 000 = 1,024 × 10 6

Отбрасывать можно только те нули, которые располагаются в конце, и после которых нет других цифр, бóльших нуля. В приведённом примере были отброшены только три нуля, а нуль располагавшийся между запятой и цифрой 2 был сохранен, несмотря на то, что он тоже располагался после запятой.

Пример 6. Записать число 0,000325 в стандартном виде.

Источник

Общий взгляд на преобразование дробей

Данный обобщенный материал известен из школьного курса математики. Тут рассматриваем дроби общего вида с числами, степенями, корнями, логарифмами, тригонометрическими функция ми или другими объектами. Будут рассмотрены основные преобразования дробей вне зависимости от их вида.

Что такое дробь?

Существует еще несколько определений.

Выражение, которое находится над чертой дроби, называют числителем, а под – знаменателем.

От обыкновенных дробей к дробям общего вида

Знакомство с дробью происходит еще в 5 классе, когда проходят обыкновенные дроби. Из определения видно, что числителем и знаменателем являются натуральные числа.

После изучения действий с обыкновенными дробями имеем дело с дробями, которые имеют в знаменателе не одно натуральное число, а выражения с натуральными числами.

Когда имеем дело с дробями, где есть буквы или буквенные выражения, то записывается таким образом:

Черта дроби расценивается как знак деления. Поэтому запись можно преобразовать по-другому:

Вычисления с рациональными дробями занимают особое место в математике, так как в числителе и знаменателе могут быть не просто числовые значения, а многочлены.

Рациональные выражения рассматриваются как дроби общего вида.

Изучение корней, степеней с рациональными показателями, логарифмов, тригонометрических функций говорит о том, что их применение появляется в заданных дробях вида:

Виды преобразований дробей

Для ряда тождественных преобразований рассматривают несколько видов:

Преобразование выражений в числителе и знаменателе

При тождественно равных выражениях имеем, что полученная дробь является тождественно равной исходной.

Имеем, что A и A 1 и B и B 1 тождественно равны, тогда их значения тоже равны. Отсюда следует, что при любом их значении A / B и A 1 / B 1 данные дроби будут равны.

Такое преобразование упрощает работу с дробями, если необходимо преобразовывать отдельно числитель и отдельно знаменатель.

Изменение знака перед дробью, в ее числителе, знаменателе

Преобразования дробей – это также и замена знаков перед дробью. Рассмотрим некоторые правила:

После доказательства первого утверждения, обосновываем оставшиеся. Получим:

Преобразования выполняются следующим образом:

Приведение дроби к новому знаменателю

Отсюда видно, что преобразования основываются на 2 преобразованиях: приведении к общему знаменателю, сокращении.

При приведении к общему знаменателю производится умножение на одно и то же число или выражение числитель и знаменатель. То есть мы переходим к решению тождественной равной преобразованной дроби.

Такое преобразование как избавление от иррациональности в знаменателе также применимо. Оно избавляет от наличия корня в знаменателе, что упрощает процесс решения.

Сокращение дробей

Основное свойство – это преобразование, то есть ее непосредственное сокращение. При сокращении мы получаем упрощенную дробь. Рассмотрим на примере:

Сокращение дроби является простым, когда общие множители сразу явно видны. Практически это встречается не часто, поэтому предварительно необходимо проводить некоторые преобразования выражений такого вида. Бывают случаи, когда необходимо находить общий множитель.

Представление дроби в виде суммы

Данное преобразование в корне отличается от сложения дробей с одинаковыми показателями. Рассмотрим пример.

Разложение дроби на простейшие является частным случаем для преобразования дроби в сумму. Чаще всего его применяют при сложных вычислениях для интегрирования.

Источник