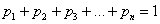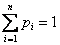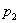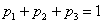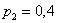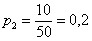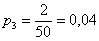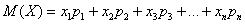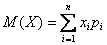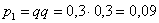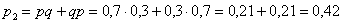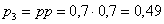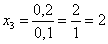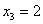Математическое ожидание и дисперсия что это

Числовые характеристики распределения вероятностей. Математическое ожидание, дисперсия и стандартное отклонение

п.1. Закон распределения дискретной случайной величины

п.2. Математическое ожидание

Свойства математического ожидания
1) Размерность математического ожидания равна размерности случайной величины.
2) Математическое ожидание может быть любым действительным числом: положительным, равным 0, отрицательным.
3) Математическое ожидание постоянной величины равно этой постоянной:

4) Математическое ожидание суммы независимых случайных величин равно сумме математических ожиданий:

5) Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий:

6) Постоянный множитель можно вынести за знак математического ожидания:

Например:
Пусть в результате экспериментов получено следующее распределение случайной величины X – числа появления белых шаров (см. пример 1, §40 данного справочника):

Найдём математическое ожидание для данного распределения:

п.3. Дисперсия

Свойства дисперсии
1) Размерность дисперсии равна квадрату размерности случайной величины.
2) Дисперсия может быть любым неотрицательным действительным числом.
3) Дисперсия постоянной величины равна нулю:

4) Дисперсия суммы независимых случайных величин равна сумме дисперсий:

5) Постоянный множитель можно вынести за знак дисперсии:

Например:
Продолжим исследование и найдём дисперсию для распределения случайной величины X – числа появления белых шаров. Составим расчётную таблицу:

Получаем: D(X) = 10,9375 – 3,125 2 ≈ 1,1719.

п.4. Среднее квадратичное отклонение

Свойства СКО
1) Размерность СКО равна размерности случайной величины.
2) СКО может быть любым неотрицательным действительным числом.
3) СКО постоянной величины равно нулю:

4) Постоянный множитель можно вынести за знак СКО:

п.5. Правило трёх сигм

Большое количество случайных величин, измеряемых в экспериментах (например, в школьных лабораторных работах), имеет так называемое нормальное распределение.
В частности, при больших n, биномиальное распределение можно с хорошей точностью описывать как нормальное с M(X) = np и \(\mathrm<\sigma(X)=\sqrt>\).
График плотности нормального распределения p(x) похож на колокол, с максимумом, соответствующим M(X) = X_cp – среднему значению измеряемой величины.

Величина СКО σ(X) характеризует степень отклонения X от среднего значения M(X).

п.6. Примеры

Пример 1. Найдите математическое ожидание, дисперсию и СКО при бросании кубика.

Закон распределения величины X – очки на верхней грани при бросании кубика и расчётная таблица:

Пример 2*. Найти математическое ожидание, дисперсию и СКО суммы очков при бросании двух кубиков.

Пример 3*. Докажите, что в опытах по схеме Бернулли математическое ожидание M(X)=np, а дисперсия D(X)=npq.

Проведем один опыт. В нём может быть только два исхода: «успех» и «неудача».
Составим расчётную таблицу:

Мат.ожидание первого опыта \(\mathrm\).
Общее число успехов при n опытах складывается из числа успехов при каждом опыте, т.е. \(\mathrm\). Все опыты между собой независимы.
По свойству мат.ожидания суммы независимых событий: \begin \mathrm< M(X)=M(X_1+X_2+. +X_n)=M(X_1)+M(X_2)+. +M(X_n)= >\\ \mathrm<=\underbrace_>=np > \end Дисперсия первого опыта \(\mathrm\)
По свойству дисперсии суммы независимых событий: \begin \mathrm< D(X)=D(X_1+X_2+. +X_n)=D(X_1)+D(X_2)+. +D(X_n)= >\\ \mathrm<=\underbrace_>=npq > \end Что и требовалось доказать.

Пример 4. 100 канцелярских кнопок высыпали на стул. Вероятность, что кнопка упала острием вверх, равна 0,4. Найдите среднее количество, дисперсию и СКО для числа кнопок, упавших острием вверх. Найдите интервал оценки для количества этих кнопок по правилу «трёх сигм».

По условию n = 100, p = 0,4.
Для каждой кнопки может быть два исхода: упасть острием вверх или вниз.
Таким образом, это испытание Бернулли с биномиальным распределением случайной величины. \begin \mathrm< M(X)=np=100\cdot 0,4=40 >\\ \mathrm\\ \mathrm<\sigma(X)=\sqrt=\sqrt<24>\approx 4,9> \end Интервал оценки «три сигмы»: \begin \mathrm< M(X)-3\sigma(X)\lt X\lt M(X)+3\sigma(X) >\\ \mathrm<40-3\cdot 4,9\lt X\lt 40+3\cdot 4,9 >\\ \mathrm<25,3\lt X\lt 54,7>\\ \mathrm <26\leq X\leq 54>\end Скорее всего (99,7%), от 26 до 54 кнопок будут острием вверх.
Ответ: \(\mathrm\)

Пример 5*. В тесте 10 задач с 4 вариантами ответов. Ответы выбираются наугад. Постройте распределение величины X = «количество угаданных ответов», найдите числовые характеристики этого распределения.
Найдите интервал оценки для количества угаданных ответов по правилу «трёх сигм».
Какова вероятность угадать хотя бы 1 ответ? Хотя бы 5 ответов? Угадать все 10 ответов?

Вероятность угадать хотя бы один ответ: \begin \mathrm< P(X\geq 1)=1-p_0\approx 1-0,0563=0,9437 >\end Очень хорошие шансы – 94,37%.
Вероятность угадать хотя бы 5 ответов: \begin \mathrm< P(X\geq 5)=1-\left(\sum_^<4> \right)\approx 1-(0,0563+0,1877+. +0,1460)=0,0781 >\end Шансов мало – 7,81%. Т.е. «средний балл» при сдаче тестов мало достижим методом научного тыка.
Вероятность угадать все 10 ответов: p₁₀≈ 0,000001. Шанс – один из миллиона.

Источник

Случайные величины. Дискретная случайная величина.
Математическое ожидание

Второй раздел по теории вероятностей посвящён случайным величинам, которые незримо сопровождали нас буквально в каждой статье по теме. И настал момент чётко сформулировать, что же это такое:

Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.

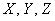
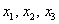
Случайные величины, как правило, обозначают через *, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .

* Иногда используют 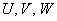, а также греческие буквы

Пример встретился нам на первом же уроке по теории вероятностей, где мы фактически рассмотрели следующую случайную величину:

– количество очков, которое выпадет после броска игрального кубика.

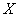
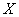
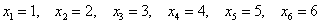
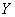
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина может принять одно из следующий значений:

.

– количество мальчиков среди 10 новорождённых.

Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться:

, либо мальчиков – один и только один из перечисленных вариантов.

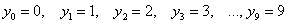
И, дабы соблюсти форму, немного физкультуры:

– дальность прыжка в длину (в некоторых единицах).

Её не в состоянии предугадать даже мастер спорта 🙂

Тем не менее, ваши гипотезы?

Коль скоро речь идёт о множестве действительных чисел, то случайная величина 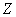может принять несчётно много значений из некоторого числового промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.

Таким образом, случайные величины целесообразно разделить на 2 большие группы:

1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.

…нарисовались непонятные термины? Срочно повторяем основы алгебры!

2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.

Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ

Сначала разберём дискретную случайную величину, затем – непрерывную.

Закон распределения дискретной случайной величины

– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:

Довольно часто встречается термин ряд распределения, но в некоторых ситуациях он звучит двусмысленно, и поэтому я буду придерживаться «закона».

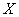
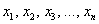
А теперь очень важный момент: поскольку случайная величина обязательно примет одно из значений , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:

или, если записать свёрнуто:

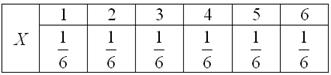
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:

Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:

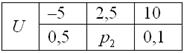
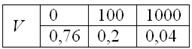
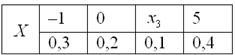
Некоторая игра имеет следующий закон распределения выигрыша:

Найти

…наверное, вы давно мечтали о таких задачах 🙂 Открою секрет – я тоже. В особенности после того, как завершил работу над теорией поля.

Решение: так как случайная величина 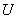может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:

Разоблачаем «партизана»: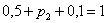

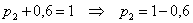
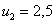
– таким образом, вероятность выигрыша условных единиц составляет 0,4.

Контроль: 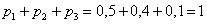, в чём и требовалось убедиться.

Ответ:

Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий и другие фишки тервера:

В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины 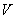– размера выигрыша, если из коробки наугад извлекается один билет.

Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно 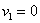рублей.

Всего таковых билетов 50 – 12 = 38, и по классическому определению:
– вероятность того, что наудачу извлечённый билет окажется безвыигрышным.

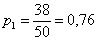
С остальными случаями всё просто. Вероятность выигрыша 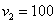рублей составляет:

И для :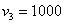

Проверка: 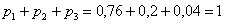– и это особенно приятный момент таких заданий!

Ответ: искомый закон распределения выигрыша:

Следующее задание для самостоятельного решения:

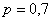
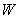
Вероятность того, что стрелок поразит мишень, равна . Составить закон распределения случайной величины – количества попаданий после 2 выстрелов.

…я знал, что вы по нему соскучились 🙂 Вспоминаем теоремы умножения и сложения. Решение и ответ в конце урока.

Закон распределения полностью описывает случайную величину, однако на практике бывает полезно (а иногда и полезнее) знать лишь некоторые её числовые характеристики.

Математическое ожидание дискретной случайной величины

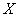
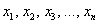
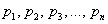
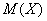
Говоря простым языком, это среднеожидаемое значение при многократном повторении испытаний. Пусть случайная величина принимает значения с вероятностями соответственно. Тогда математическое ожидание данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:

или в свёрнутом виде:

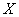
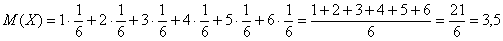
Вычислим, например, математическое ожидание случайной величины – количества выпавших на игральном кубике очков:

очка

В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близкО к 3,5 – и чем больше провести испытаний, тем ближе. Собственно, об этом эффекте я уже подробно рассказывал на уроке о статистической вероятности.

Теперь вспомним нашу гипотетическую игру:

Возникает вопрос: а выгодно ли вообще играть в эту игру? …у кого какие впечатления? Так ведь «навскидку» и не скажешь! Но на этот вопрос можно легко ответить, вычислив математическое ожидание, по сути – средневзвешенный по вероятностям выигрыш:

, таким образом, математическое ожидание данной игры проигрышно.

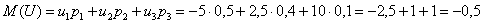
Не верь впечатлениям – верь цифрам!

Да, здесь можно выиграть 10 и даже 20-30 раз подряд, но на длинной дистанции нас ждёт неминуемое разорение. И я бы не советовал вам играть в такие игры 🙂 Ну, может, только ради развлечения.

Из всего вышесказанного следует, что математическое ожидание – это уже НЕ СЛУЧАЙНАЯ величина.

Творческое задание для самостоятельного исследования:

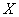
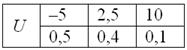
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?

Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино

Существует много других систем игры в рулетку, для которых можно составить свои таблицы вероятностей. Но это тот случай, когда нам не нужны никакие законы распределения и таблицы, ибо доподлинно установлено, что математическое ожидание игрока будет точно таким же. От системы к системе меняется лишь дисперсия, о которой мы узнаем во 2-й части урока.

Но прежде будет полезно размять пальцы на клавишах калькулятора:

Случайная величина 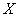задана своим законом распределения вероятностей:

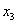
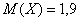
Найти , если известно, что . Выполнить проверку.

Тогда переходим к изучению дисперсии дискретной случайной величины, и по возможности, ПРЯМО СЕЙЧАС!! – чтобы не потерять нить темы.

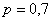
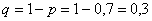
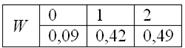
Пример 3. Решение: по условию – вероятность попадания в мишень. Тогда:
– вероятность промаха.

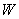
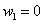
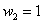
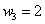
Составим – закон распределения попаданий при двух выстрелах:

– ни одного попадания. По теореме умножения вероятностей независимых событий:

– одно попадание. По теоремам сложения вероятностей несовместных и умножения независимых событий:

– два попадания. По теореме умножения вероятностей независимых событий:

Проверка: 0,09 + 0,42 + 0,49 = 1

Ответ:

Примечание: можно было использовать обозначения 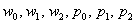– это не принципиально.

Пример 4. Решение: игрок выигрывает 100 рублей в 18 случаях из 37, и поэтому закон распределения его выигрыша имеет следующий вид: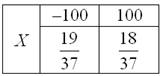

Вычислим математическое ожидание: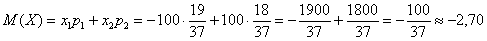

Таким образом, с каждой поставленной сотни игрок в среднем проигрывает 2,7 рубля.

Пример 5. Решение: по определению математического ожидания: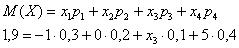

поменяем части местами и проведём упрощения: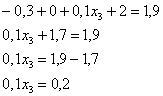

таким образом:

Выполним проверку: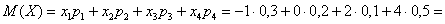

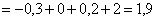
, что и требовалось проверить.

Ответ:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник