Математика и высшая математика в чем разница

Прикладная или фундаментальная: какой считают в мире математику

Можно ли считать математику фундаментальной наукой или это всего лишь инструмент, как писал советский математик Колмогоров, на службе у естественных наук — этот вопрос остается открытым. Даже сами математики отказываются однозначно отвечать на него. Методист по математике Университета Иннополис Дмитрий Бебчук рассказал на фестивале науки и технологии «ПРОСТО», организованном российским ИТ-вузом, о том, какие изобретения человечества были бы невозможны без математики и почему математизирование — это процесс творческий, не требующий никаких практических целей.

Читайте «Хайтек» в

Наука о структурах или просто расчеты?

« Британника» говорит, что математика — это наука о структурах, порядках и отношениях, возникшая из элементарных практик подсчета, измерения и описания форм объектов. Она строится на логических рассуждениях и количественных расчетах. Группа французских математиков, которые взяли себе в 1935 году коллективный псевдоним Никола Бурбаки, предложила такое определение: математика — это наука об отношениях между объектами, о которых ничего не известно, кроме их свойств. именно ими объекты и описываются. Может возникнуть двоякое впечатление. С одной стороны, у нас есть конструктивное определение математики, а с другой, математика — это когда «взяли что-то и посчитали». Этот своеобразный конфликт выразился в том числе в установлении теории множеств. Есть аксиоматика Сернела Френкеля, которая являет собой конструктивный подход к теории множеств, но существуют и альтернативы. Это всё возникло из-за парадокса Рассела.

Парадокс Рассела — открытый в 1901 году Бертраном Расселом теоретико-множественный парадокс (антиномия), демонстрирующий противоречивость логической системы Фреге, являвшейся ранней попыткой формализации наивной теории множеств Георга Кантора.

Парадокс можно описать следующим образом. Условимся называть множество «обычным», если оно не является своим собственным элементом. Например, множество всех людей является «обычным», так как само множество — не человек. Примером «необычного» множества является множество всех множеств, так как оно само является множеством, а, следовательно, само является собственным элементом.

Система аксиом Цермело — Френкеля (ZF) — наиболее широко используемый вариант аксиоматической теории множеств. Сформулирована Эрнстом Цермело в 1908 году для преодоления парадоксов теории множеств, а затем была уточнена Абрахамом Френкелем в 1921 году. Система аксиом записана на языке логики первого порядка.

Я попытаюсь вам доказать, что математика — это фундаментальная наука. Фундаментальная наука должна обладать следующими свойствами: ее результаты должны быть универсальны; в ее задачи не должна входить изначально практическая реализация полученных результатов; и она позволяет нам получать новые знания о природе, то есть иметь предсказательную силу.

В универсальности результатов математики сомнений нет. Это самый легкий пункт, поэтому он стоит первым. Действительно, даже на уровне «дважды два — четыре»: в любое время и на любом континенте это будет, конечно же, четыре.

Как из чистых идей родились практические инструменты

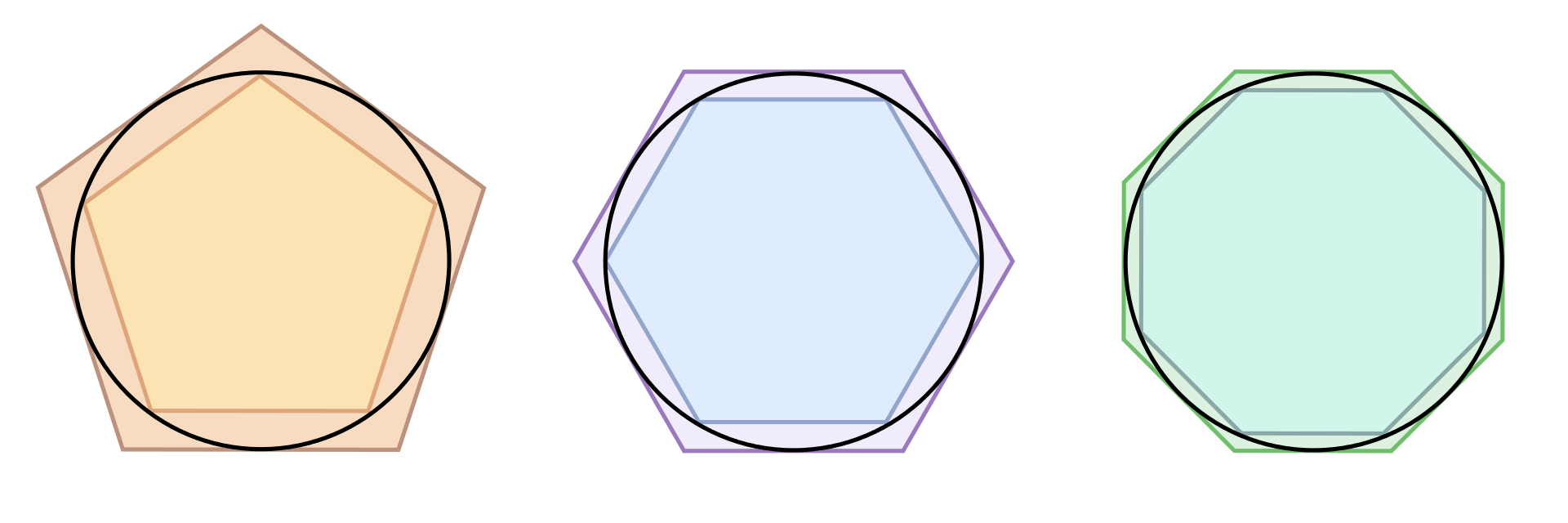
Существуют четыре области математики, которые развились из совершенно абстрактной идеи. Во-первых, анализ бесконечно малых, то, что сейчас называют математическим анализом. Началось всё с того, что предположительно Антифон в V веке до нашей эры предложил метод исчерпывания. Он и сейчас так называется. С помощью этого метода можно находить площадь фигур, границы которых — не отрезки. Например, площадь круга. Если есть круг, то его можно заключить, например, в пятиугольник, а также вписать в него пятиугольник. Площадь круга получится чем-то средним между ними. Если заменить пятиугольник на шести-, семи- и восьмиугольник, то точность приближения возрастет. Чем больше количество сторон у нашего вот многоугольника, который вписан и описан около круга, тем лучше оказывается наше приближение.

Но площадь круга пропорциональна квадрату радиуса, а коэффициент пропорциональности — это какое-то число. Были предложены оценки этого числа: например, Архимед предположил, что это примерно 22/7, эта оценка позволяет нам получить точность до двух знаков после десятичной запятой. А пресловутый Цзу Чунжи уже предложил оценку намного лучше: 355/113, уже шесть знаков после запятой. В конце концов, было доказано, что пи — это число иррациональное и даже трансцендентное, то есть не является алгебраическим числом.

Цзу Чунжи — китайский математик и астроном. Как астроном определил сидерические периоды обращения планет Солнечной системы с высокой точностью. Разработал новый календарь с учетом явления прецессии. Как математик первым в мире рассчитал число пи с точностью до седьмого знака после запятой, дав его значение между 3,1415926 и 3,1415927; более точное значение было вычислено лишь тысячу лет спустя.

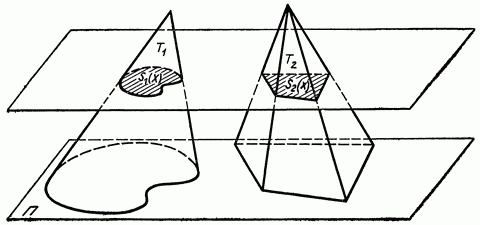
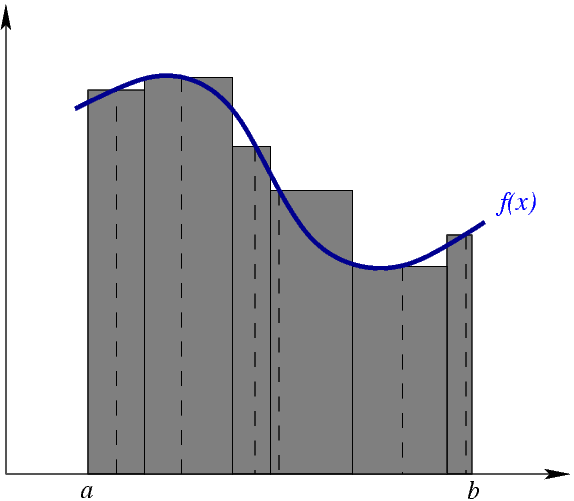
Принцип Кавальери очень прост: если у вас есть два объемных тела одинаковой высоты и на каждом уровне площади иссечений одинаковы, то и объемы этих тел одинаковы. Такой принцип подходит для нахождения объемов тел, у которых грани необязательно плоские. Например, конус. Из таких совершенно теоретических подходов к XVII веку уже развивается дифференциальное и интегральное исчисление, у истоков которого стоят двое ученых — Ньютон и Лейбниц, которые примерно одновременно развивали эту область. Практическое применение их работ сегодня: поиск длины кривой и касательной к сфере, дивергенции, роторы и даже двумерное нормальное распределение, благодаря которому можно искать вероятности сложноконструируемых событий.

Бонавентура Кавальери — итальянский математик, предтеча математического анализа, наиболее яркий и влиятельный представитель «геометрии неделимых». Выдвинутые им принципы и методы позволили еще до открытия математического анализа успешно решить множество задач аналитического характера.

В XVI веке Джероламо Кардано ввел понятие комплексного числа. В его трудах комплексные числа описаны как совершенно утонченные и бесполезные структуры, утонченные — это позитивная характеристика, а бесполезные — ну мы понимаем. Он не видел им совершенно никакого применения, но, тем не менее, пытался развивать эту теорию. Уже потом стало ясно, что это полезный инструмент для многих областей. Альберт Эйнштейн согласился бы. В качестве примеров — расчёт электрических цепей переменного тока, который делается гораздо проще с применением комплексно-значимых функций. Всяческие теоремы о распределении простых чисел — небезызвестная дзета-функция Римана и теорема, связанная с ней, гипотеза, на самом деле, потому что она еще не доказана — это одна из семи проблем тысячелетия. Гиперкомплексные числа, так называемые кватернионы, нашли свое применение в позиционировании. Тут меня поймут робототехники. Когда мы определяем или задаем положение трехмерного объекта в пространстве, то кватернионы исключительно полезны. А обойтись без выхода в это гиперкомплексное пространство нам уже тяжелее.

Джероламо Кардано — итальянский математик, инженер, философ, врач и астролог. В его честь названы открытые Сципионом дель Ферро формулы решения кубического уравнения (Кардано был их первым публикатором), карданов подвес, карданный вал и решетка Кардано.

Кватернионы — система гиперкомплексных чисел, образующая векторное пространство размерностью четыре над полем вещественных чисел. Предложены Уильямом Гамильтоном в 1843 году.

Некоторые алгоритмы шифрования основаны на свойствах эллиптических кривых, а, точнее, на их алгебраических свойствах. Но всё началось с того, что Диофант Александрийский в III веке нашей эры пытался найти решение этого уравнения: y*(6-y)=x3-x. В конце XVII — начале XVIII века Ньютон тоже пытался его решить. Все вылилось в целую теорию, которая позволяет нам достаточно быстро зашифровать данные, с тем, чтобы их расшифровка требовала существенно больше времени. То есть мы получаем криптографически такой механизм — алгоритм.

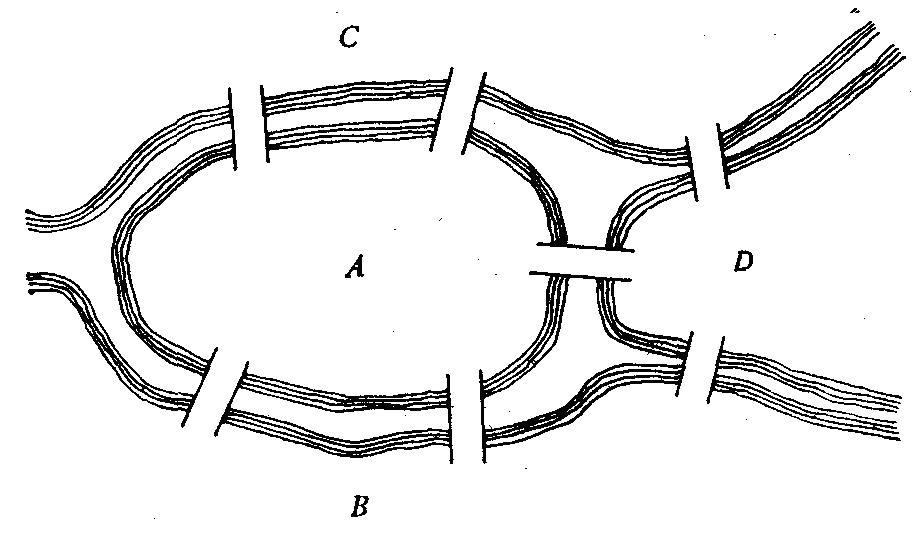
Задачу мостов Эйлера: существует ли маршрут, чтобы обойти каждый мост Кенигсберга только по одному разу, — сегодня может решить почти любой олимпиадник. Этот вопрос XVIII века, тогда еще практически неприменимый, породил целую область математики — топологию. Сегодня она применяется, например, в робототехнике. У манипулятора есть конфигурационное пространство. Например, у двухзвенного манипулятора — это тор. Но тор — это определенный топологический объект: если мы возьмем две точки на торе, то сможем сказать про траекторию передвижения между этими двумя точками, про минимальность и так далее. То есть появляется целая область для анализа. А если манипулятор трехзвенный, то и поверхность становится значительно сложнее, а задача по нахождению какого-то оптимального пути или даже просто нахождению пути — на порядки. Тут без топологии уже не обойтись.

Анализ бесконечно малых, топология, эллиптические кривые — все это доказывает то, что в развитие этих областей было вовлечено много людей. А после XVIII века математика уже становится профессиональный наукой, то есть человек со стороны практически не имеет шансов добиться в ней значимых на мировом уровне успехов. Второй тезис, получается, доказан. Эти люди занимались математикой всю жизнь, не надеясь на то, что их конкретные результаты будут практически применимыми.

Как способ описать природу

Пресловутый Бозон Хиггса, который, конечно, прежде чем был обнаружен и зафиксирован, сначала был рассчитан. То есть была целая теория, основанная на расчетах. Теория, согласно которой такая частица должна существовать и должна обладать определенными свойствами. Это доказывает, что математика позволяет получать новые знания о природе. Вернемся к самому началу: что математика — это наука о неких структурах, у которых мы знаем только свойства, а потом уже смотрим, а что же из этого получается. Бозон Хиггса, который тогда еще не знали, но уже по предположениям ученых должен был обладать определенными свойствами.

Второй пример — девятая планета. Российский ученый Батыгин, который сейчас преподает в США, сначала вычислил орбиту девятой планеты, прежде чем ее обнаружили. То есть, согласно каким-то расчетам, эта планета должна была существовать, а потом она уже была обнаружена в расчетной точке.

Получается, что математика — фундаментальная наука. Но многие скажут, что математика — это просто дисциплина на службе естественных наук, и отчасти они будут правы. И с ними согласился бы даже Колмогоров, который в предисловии к книге Куранта и Роббинса так и сказал, что математика неотделима от ее практических применений.

Андрей Колмогоров — советский математик, один из основоположников современной теории вероятностей, им получены фундаментальные результаты в топологии, геометрии, математической логике, классической механике, теории турбулентности, теории сложности алгоритмов, теории информации, теории функций и в ряде других областей математики и ее приложений.

Рихард Курант — немецкий и американский математик, педагог и научный организатор. Известен как автор классической популярной книги по математике «Что такое математика?», а также как один из авторов критерия Куранта — Фридрихса — Леви.

Герберт Роббинс — американский математик и статистик. Его именем названы лемма Роббинса, алгебра Роббинса, теорема Роббинса и другие термины.

Вейль говорит о том, что вопрос об основаниях математики и о том, что в конечном счете она собой представляет, остается открытым. И неизвестно такого направления, которое позволит в конце концов найти окончательный ответ на этот вопрос. Можно ли ожидать, что он когда-нибудь будет получен и признан всеми математиками? Вейль указывает на то, что сам процесс изучения математики, математизирование — это творческий процесс, когда люди, не надеясь на практическое применение их результатов, результатов их работы, просто занимаются этим процессом. Но а то, что он описывает мир, надеюсь, я вас убедил, тут сомнений уже нет. Математика действительно описывает мир, и нет естественной науки, которая не пользовалась бы математическим аппаратом. В современном мире и общественные науки, в том числе социология, пользуются математическими методами как методами для исследования.

Андре Вейль — французский математик, внесший значительный вклад в алгебраическую геометрию и топологию, член группы Бурбаки. Важнейшие труды в области алгебраической геометрии, которую сумел обосновать с нужным уровнем строгости, получил важные результаты в функциональном анализе, в частности в теории меры и интегрирования в топологических группах и теории чисел, к которой применил аппарат гомологической алгебры и функционального анализа.

Источник

Математика – это фундаментальная наука, которая занимается изучением разных структур, их отношений и порядков. Математика, как наука, появилась очень давно, наверное, с возникновением человечества. Уже в раннем палеолите люди были знакомы с основами счета. У людей всегда была необходимость что-то подсчитать или пересчитать. Известно, что для счета люди пользовались и пальцами, и камнями, и палками и различными метками. Историю развития математики отсчитывают именно с того момента, как люди научились считать.

Для того чтобы понять, чем отличается прикладная математика от математики, нужно рассмотреть основные понятия, которыми оперирует одна и вторая наука.

Математика

Если посмотреть определение математики в различных словарях и энциклопедиях, то можно заметить, что единого точного определения математики не существует. Однако мы все интуитивно понимаем, что такое математика. Наилучшее определение было дано, наверное, Бурбаки.

Бурбаки – это псевдоним группы математиков, которые написали серию книг по математике. По определению Бурбаки, математика изучает отношения между какими-то объектами. Каждый объект описывается с точки зрения его количественных характеристик. Сущностью математики является описание некоторого набора абстрактных структур.

Из этого определения становится понятно, чем занимается теоретическая математика. Она должна описать отношения различных структур данных.

Математика делится на элементарную и высшую части. Элементарную математику изучают в школе.

Элементарная математика включает в себя такие разделы, как:

Геометрия

Высшая математика состоит из:

В теоретической математике разработан математический аппарат, основу которого составляют обозначения, аксиомы, утверждения. А на базе уже этого аппарата развивается дальнейшая теория, доказываются теоремы и выводятся определенные правила.

Наука математика

Например, в математическом анализе используются такие понятия, как бесконечно малая величина, дифференциал, функция. Алгебра оперирует понятиями множество, группа, кольцо и т.д. Дифференциальные уравнения работают с производной и интегралом. Таким образом, видно, что теоретическая математика разрабатывает некий понятийный аппарат. Английский математик Годфри Харди говорил, что чистая математика не приносит никакой практической пользы.

Прикладная математика

Прикладная математика является частью математики. Если говорить обычным языком, прикладная математика – это математика, которая используется на практике. Прикладная математика изучает и разрабатывает способы применения теоретической математики в других дисциплинах. Если вернуться к словам математика Харди, то в отличие от чистой математики, прикладная математика приносит практическую польз

Разделы прикладной математики

Предметом исследования прикладной математики является применение теоретических математических методов чистой математики в других науках. Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.

Использование прикладной математики

В физике или химии для проведения каких-либо экспериментов или опытов, не всегда представляется возможным провести испытания на реальном объекте. Поэтому строится его модель. Модель – это уменьшенная или увеличенная копия реального объекта, которая имеет точно такие же свойства.

Модели бывают математическими. Модель может быть создана и на компьютере с помощью графических редакторов. Моделирование разных физических или химических процессов заканчивается решением с использованием численных методов.

Криптография – это наука, которая занимается шифрованием. В шифровании используются различные математические методы и алгоритмы.

Таким образом, из вышеприведенного понятно, что и чистая математика, и прикладная математика использует одни и те же методы. Но чистая математика использует эти методы для дальнейшего развития теории, а прикладная математика использует математические методы и теорию чистой математики для того, чтобы можно было решать реальные задачи в физике, химии, биологии, статистике, экономике и в других науках.

Источник

Чем отличается математика от прикладной математики

Математика – это фундаментальная наука, которая занимается изучением разных структур, их отношений и порядков. Математика, как наука, появилась очень давно, наверное, с возникновением человечества. Уже в раннем палеолите люди были знакомы с основами счета. У людей всегда была необходимость что-то подсчитать или пересчитать. Известно, что для счета люди пользовались и пальцами, и камнями, и палками и различными метками. Историю развития математики отсчитывают именно с того момента, как люди научились считать.

Для того чтобы понять, чем отличается прикладная математика от математики, нужно рассмотреть основные понятия, которыми оперирует одна и вторая наука.

Математика

Если посмотреть определение математики в различных словарях и энциклопедиях, то можно заметить, что единого точного определения математики не существует. Однако мы все интуитивно понимаем, что такое математика. Наилучшее определение было дано, наверное, Бурбаки.

Бурбаки – это псевдоним группы математиков, которые написали серию книг по математике. По определению Бурбаки, математика изучает отношения между какими-то объектами. Каждый объект описывается с точки зрения его количественных характеристик. Сущностью математики является описание некоторого набора абстрактных структур.

Из этого определения становится понятно, чем занимается теоретическая математика. Она должна описать отношения различных структур данных.

Математика делится на элементарную и высшую части. Элементарную математику изучают в школе.

Она включает в себя такие разделы, как:

Высшая математика состоит из:

В теоретической математике разработан математический аппарат, основу которого составляют обозначения, аксиомы, утверждения. А на базе уже этого аппарата развивается дальнейшая теория, доказываются теоремы и выводятся определенные правила.

Прикладная математика

Прикладная математика является частью математики. Если говорить обычным языком, прикладная математика – это математика, которая используется на практике. Прикладная математика изучает и разрабатывает способы применения теоретической математики в других дисциплинах. Если вернуться к словам математика Харди, то в отличие от чистой математики, прикладная математика приносит практическую пользу.

Разделы прикладной математики

Предметом исследования прикладной математики является применение теоретических математических методов чистой математики в других науках. Например, строятся экономические модели и с помощью методов теории оптимального управления вырабатываются наилучшие управленческие решения.

В физике или химии для проведения каких-либо экспериментов или опытов, не всегда представляется возможным провести испытания на реальном объекте. Поэтому строится его модель. Модель – это уменьшенная или увеличенная копия реального объекта, которая имеет точно такие же свойства.

Криптография – это наука, которая занимается шифрованием. В шифровании используются различные математические методы и алгоритмы.

Таким образом, из вышеприведенного понятно, что и чистая математика, и прикладная математика использует одни и те же методы. Но чистая математика использует эти методы для дальнейшего развития теории, а прикладная математика использует математические методы и теорию чистой математики для того, чтобы можно было решать реальные задачи в физике, химии, биологии, статистике, экономике и в других науках.

Источник

Математика и высшая математика в чем разница

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

Доцент

Группа: Преподаватели
Сообщений: 3 615
Регистрация: 27.2.2007
Город: Екатеринбург
Вы: преподаватель

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

А можно ли обойтись без понятия «предела»?

А почему нельзя определить их, например, через суммирование атомов, других квантов пространства?
Древние греки как SIN и COS определяли?

Доцент

Группа: Преподаватели
Сообщений: 3 615
Регистрация: 27.2.2007
Город: Екатеринбург
Вы: преподаватель

определение предела является трехуровневым, так как содержит три квантора: для любого, существует, для любого.

Поэтому оно считается сложным для восприятия. В школьной математике в основном одноуровневые определения.

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

определение предела является трехуровневым, так как содержит три квантора: для любого, существует, для любого.

Поэтому оно считается сложным для восприятия. В школьной математике в основном одноуровневые определения.

Можно ли обойтись без понятия «предела»?

Есть ли альтернативы Теории Множеств с ее «кванторами»? Почему о них умалчивают?

Доцент

Группа: Преподаватели
Сообщений: 3 840
Регистрация: 27.9.2007
Из: Старый Оскол
Город: Москва
Учебное заведение: МФТИ/МАИ
Вы: другое

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

А что с дискретным анализом?

Доцент

Группа: Преподаватели
Сообщений: 3 840
Регистрация: 27.9.2007
Из: Старый Оскол
Город: Москва
Учебное заведение: МФТИ/МАИ
Вы: другое

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

Вы видели на практике «непрерывные» платонические объекты?

Даже сам основатель высшей математики, Кантор, был шизофреником:

Должны ли мы ему уподобляться?

Доцент

Группа: Преподаватели
Сообщений: 3 840
Регистрация: 27.9.2007
Из: Старый Оскол
Город: Москва
Учебное заведение: МФТИ/МАИ
Вы: другое

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

Теория расходящаяся с реальностью лженаучна.

В каком коллайдере Вы выявилили бесконечно малые имматериальные точки?

Доцент

Группа: Преподаватели
Сообщений: 3 840
Регистрация: 27.9.2007
Из: Старый Оскол
Город: Москва
Учебное заведение: МФТИ/МАИ
Вы: другое

Новичок

Группа: Продвинутые
Сообщений: 8
Регистрация: 17.6.2011
Город: Бирабиджан

Электромагнитные волны видны с помощью приборов. А какой прибор позволяет увидеть «бесконечное множество»?

Разве теорию нельзя заменить практикой?

Источник