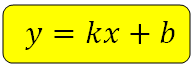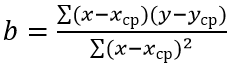Можно ли сказать что тангенс угла наклона

§ 4. Равномерное прямолинейное движение. Скорость. Уравнение движения (окончание)

Выберем оси координат так, чтобы точка двигалась по какой-либо оси, например по оси ОХ. Тогда векторы ₀ и будут составлять с осями OY и OZ прямой угол. Поэтому их проекции на эти оси равны нулю. А значит, равны нулю в любой момент времени и проекции радиус-вектора ₀ на оси OY и OZ. Так как проекции радиус- вектора на координатные оси равны координатам его конца, то r_х = х и r_0х = х₀. Поэтому в проекциях на ось ОХ уравнение (1.4) можно записать в виде

Запомни
Уравнение (1.5) есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме.

Оно позволяет найти координату х точки при этом движении в любой момент времени, если известны проекция её скорости на ось ОХ и её начальная координата х₀.

Если ₀ и не совпадают по направлению, а ось ОХ направлена вдоль скорости, то уравнение движения запишем в виде

x = x₀ + _xt
y = y₀
z = z₀,

где х₀, у₀, z₀ — проекции радиус-вектора ₀ на оси координат (рис. 1.10, а).

Какое из наблюдаемых вами движений можно приблизительно считать равномерным?

Отметим, что, строго говоря, равномерного прямолинейного движения не существует. Автомобиль на шоссе никогда не едет абсолютно прямо, небольшие отклонения в ту или иную сторону от прямой всегда имеются. И значение скорости слегка изменяется. Но приближённо на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.

Графическое представление равномерного прямолинейного движения. Полученные результаты можно изобразить наглядно с помощью графиков. Особенно прост график зависимости проекции скорости от времени (рис. 1.11). Это прямая, параллельная оси времени. Площадь прямоугольника ОАВС, заштрихованная на рисунке, равна изменению координаты точки за время t. Ведь сторона ОА есть υ_x, а сторона ОС — время движения t, поэтому Δ_x = υ_xt.

На рисунке 1.12 приведены примеры графиков зависимости координаты от времени для трёх различных случаев равномерного прямолинейного движения. Прямая 1 соответствует случаю х₀ = 0, υ_x1 > 0; прямая 2 — случаю х₀ 0, а прямая 3 — случаю х₀ > 0, υ_x3 Образцы заданий ЕГЭ

A1. Зависимость координаты точки от времени при равномерном прямолинейном движении выражается

1) линейной функцией 3) тригонометрической функцией
2) квадратичной функцией 4) показательной функцией

A3. В таблице приведены координаты корабля, плывущего по прямому каналу.

Согласно данным таблицы, движение корабля является

Источник

Алгебра

Лучшие условия по продуктам Тинькофф по этой ссылке

Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера

. 500 руб. на счет при заказе сим-карты по этой ссылке

Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке

План урока:

Физический смысл производной

Вводя понятие производной, мы предварительно решали задачи на поиск мгновенной скорости некоторого тела (автомобиля, пешехода, самолета). Во всех них в качестве исходных данных задавался некоторый закон, который описывал зависимость пути, пройденного телом, от времени. Обычно этот закон представлял собой функцию s(t). Для нахождения мгновенной скорости мы сначала записывали выражение для вычисления средней скорости, которое содержало переменную величину ∆t. На следующем шаге мы составляли выражение ∆s/∆t, после чего величину ∆t мы устремляли к нулю и смотрели, чему в таком случае будет равняться предел отношения ∆s/∆t. Этот предел и принимался за мгновенную скорость тела.

Можно заметить, что последовательность наших действий совпадает с теми действиями, которые выполняются для вычисления производной. Разница лишь в обозначениях. В случае с производной мы рассматриваем функцию у(х), а в случае с поиском скорости тела – функцию s(t). Но если поменять букву t на х, а s на t, то окажется, что поиск мгновенной скорости в момент времени t₀ – это тоже самое, что и поиск производной функции s(t) в точке t₀. Таким образом, можно сформулировать физический смысл производной (иногда его называют механическим смыслом, так как в физике производная используется не только в механике):

Функцию s(t) обычно называют законом движения. Рассмотрим простейший случай, когда тело движется с постоянной скоростью, равной, например, 3 м/с. Из физики известно, что в таком случае путь s, пройденный телом за время t, можно вычислить по формуле

Значит, закон движения тела будет выглядеть так:

Найдем производную в произвольный момент времени t₀. Так как производная должна совпадать со скоростью, то независимо от значения t₀ производная должная оказаться равной 3. Действительно, в точке t₀ значение функции равно

Дадим приращение аргумента ∆t. В точке t₀ + ∆t функция будет равна

Найдем приращение функции ∆s:

Обратите внимание – величина ∆s уже не зависит от t₀. Далее найдем отношение ∆s/∆t:

Величины ∆t сократились, и получилось, что отношение ∆s/∆t от величины ∆t не зависит. Ясно, что предел этого отношения при ∆t→0 (а это и есть производная) будет равен 3:

Действительно, получилось, что производная s′(t) в любой точке равна 3, то есть она совпадает со скоростью.

Геометрический смысл производной

Возьмем график произвольной функции у(х) и выберем на ней точку х₀ (обозначим ее как А). Дадим ей приращение ∆х. Тогда мы получим новую точку с абсциссой х₀ + ∆х, которую обозначим буквой В. Соединим исходную и новую точку прямой линией АВ. Эта линия пересекает график как минимум в двух точках (А и B), поэтому мы можем назвать её секущей. Проведем также касательную к графику функции в точке А:

Если из точки B провести вертикальную линию, а из точки А – горизонтальную, то они пересекутся в некоторой точке О. Рассмотрим треугольник АОВ. Очевидно, что он прямоугольный (∠ АОВ = 90°). При этом АО = ∆х, а ОВ = ∆у. Так как АО и ОВ – это катеты прямоугольного треугольника, то их отношение (ОВ/АО) равно тангенсу угла ВАО, который на рисунке обозначен как α:

Ещё раз отметим, что угол α – это угол между секущей и горизонтальной линией. Этот угол определяется именно отношением величин ∆у и ∆х.

Производная – это предел отношения ∆у/∆х при ∆х→0. Попробуем устремить в данном случае величину ∆х к нулю. Тогда точка В начнет перемещаться по графику всё ближе к точке А, а треугольник АОВ будет сокращаться в размерах. Однако АВ всё ещё будет оставаться секущей:

Мы видим что при уменьшении ∆х секущая АВ приближается к касательной. В конце концов, при «максимальном» уменьшении ∆х, Точка В почти сольется с точкой А, а секущая АВ почти сольется с касательной. Тогда и угол α, являющийся углом наклона секущей, будет почти не отличаться (или отличаться на бесконечно малую величину) от угла наклона касательной. Поэтому можно принять, что угол α – это и есть угол наклона касательной:

Но мы уже определили ранее, что тангенс угла α – это отношение ∆у/∆х:

Получается, что в предельном случае, когда ∆х стремится к нулю, секущая, по сути, становится касательной к графику, а отношение ∆у/∆х – производной (по ее определению):

Отсюда следует, что значение производной в точке х₀ совпадает с тангенсом угла наклона касательной к графику функции в этой же точке. В этом заключается геометрический смысл производной.

Здесь следует уточнить понятие касательной. Из геометрии известно понятие касательной к окружности. Так называют прямую, имеющую с окружностью ровно одну общую точку. Однако для касательной к графику функции такое определение не подходит. Действительно, любая строго вертикальная прямая пересечет график функции только в одной точке, однако назвать ее касательной нельзя, ведь она проходит «сквозь график»:

С другой стороны, прямая, касающаяся графика в одной точке, может потом пересечь его в другой точке:

Поэтому касательную к графику в точке х₀ определяют именно как предельное положение секущей, которое получается, когда промежуток ∆х устремляют к нулю.

Задание. Найдите угол наклона касательной, проведенной к графику

в точке х₀ = 2.

Решение. Тангенс искомого угла можно найти, вычислив производную. Для этого сначала вычислим значение функции в точке х₀:

Теперь даем приращение ∆х и вычисляем функцию в точке (х₀ + ∆х):

Далее находим величину ∆у, то есть приращение функции в точке х₀:

Отношение ∆у/∆х можно определить так:

Если устремить величину ∆х к нулю, то отношение ∆у/∆х устремится к единице:

Значит, и производная в точке х₀ = 2 будет равна 1:

Производная – это тангенс угла наклона касательной, то есть

Так как тангенс 45° равен единице, то α = 45°. Убедимся в этом, проведя через точку (2; 1) прямую с таким наклоном. Она действительно оказывается касательной:

Связь производной с возрастанием и убыванием функций

Заметим, что если провести касательную к графику в той точке, где функция возрастает, то сама эта касательная окажется также возрастающей линейной функцией. При этом угол ее наклона будет острым:

Напомним что тангенс любого острого угла – это всегда положительная величина, то есть tgα > 0.

Однако это тангенс равен значению производной. Значит, она также положительна, если функция возрастает.

Ситуация меняется в случае убывающей функции. Тогда и касательная к графику оказывает убывающей линейной функцией. Из-за этого она образует с горизонтальной осью Ох не острый, а тупой угол:

Напомним, что тангенс тупого угла является отрицательным числом. Но тогда и производная должна быть отрицательная. Получается, что по знаку производной можно определить, убывает или возрастает функция в данной точке.

Задание. Определите знак производной функции у = sinx в точке х₀ = 3π/4, не вычисляя её.

Решение. График у = sinx выглядит так:

Точка х₀ = 3π/4 находится между π/2 и π. Видно, что в этой точке функция убывает. Следовательно, производная в этой точке отрицательна.

Ответ: Производная отрицательна.

Производная как функция

До этого мы вычисляли значение производной в отдельных точках графика. Она представляет некоторое число у′(х₀). Однако чаще всего производную можно вычислить в каждой точке графика у(х). То есть каждой точке х₀ соответствует какое-то число у′(х₀). Но если есть соответствие между числами х₀ или у′(х₀), то можно говорить о функции. Её обозначают как у′(х), или просто как у′.

Возникает вопрос – а как находить функцию у′(х)? Для этого можно использовать определение производной, как и в случае су′(х₀). Только вместо значения х₀ не требуется подставлять какое-то число. Продемонстрируем эту процедуру на примере.

Далее находим величину ∆ у:

Следующий шаг – вычисляем отношение ∆ у/ ∆ х:

Осталось найти предел отношения ∆ у/ ∆ х при ∆ х → 0, который и будет являться производной у′:тут что-то не поняла решение, верное?

Получили, что у′ = 2х. Ещё раз обратите внимание, что у′– это функция, а не число. Поиск производной называют операцией дифференцирования. Для краткости иногда используют такую запись:

Здесь в левой части в скобках записана исходная функция. Над скобкой стоит штрих, который и означает дифференцирование. Справа записана производная. Когда надо вычислить производную, используют такие фразы, как «продифференцируем функцию» или «возьмем производную».

Задание. Найдите производную функции у = х 2 в точке х₀ = 100.

Подставим значение х₀ = 100 в производную:

Задание. К графику у = х 2 в точках х₁ = 0,5 и х₂ = – 0,5 проведены касательные. Под каким углом пересекаются эти касательные?

Решение. Сначала приведем рисунок для этой задачи, причем выберем крупный масштаб, когда длина двух клеток равна всего 0,1:

Чтобы найти угол между двумя касательными, сначала найдем, какие углы они образуют с горизонтальной линией Ох. Для этого вычислим производную от у = х 2 в точках 0,5 и (– 0,5). Так как у′ = 2х, то

Получается, что тангенс наклона 1-ой касательной равен единице, это значит, что сам угол равен 45°. Тангенс наклона второй касательной равен (– 1). Чтобы найти угол ее наклона, составим тригонометрическое уравнение:

Естественно, уравнение имеет бесконечно большое количество решений: – π/4; 3π/4; 7π4 и т.д. Среди них нас интересует то, которое соответствует углу от 0 до 180°. Это угол 3π/4, который равен 135°.

Итак, касательные имеют углы наклона, равные 45° и 135°. Далее поиск угла их пересечения становится простой и чисто геометрической задачей. Добавим точки на рисунок:

Мы нашли, что ∠ ВСЕ = 45° и ∠ А DC = 135°. Тогда

В итоге получаем, что прямые пересекаются под прямым углом.

Ответ: 4, 6, 8 и 10 м/с.

Рассмотренный пример показывает, что зная закон движения s ( t ), можно не просто вычислить скорость тела в отдельные моменты времени, но и получить зависимость, то есть общую формулу, позволяющую вычислять скорость. Другими словами, график производной s ′( t ) совпадает с графиком скорости v ( t )

Вторая производная функции и ее физический смысл

Итак, мы узнали, что при дифференцировании функции мы получаем какую-то новую функцию. Встает логичный вопрос – а можно ли продифференцировать и эту новую функцию? Естественно можно, и в результате получат ещё одну функцию, которую называют второй производной. Для ее обозначения используют уже не один штрих, а сразу два: у′′. При необходимости можно взять и третью производную (у′′′), и четвертую (у′′′′), и даже сотую или тысячную. Однако при рассмотрении большинства практических задач достаточно первых двух производных.

Есть ли у второй производной функции физический смысл? Да. Дело в том, что в физике различают равномерное и ускоренное движение тела. В первом случае оно двигается с постоянной скоростью, а во втором скорость тела может изменяться. В связи с этим вводится и такая физическая величина, как ускорение. Она характеризует то, как быстро изменяется скорость тела. То есть ускорение – это скорость изменения скорости. Для обозначения ускорения обычно используют букву а. И для определения ускорения как раз и может потребоваться вторая производная.

Действительно, если ускорение – это скорость изменения скорости, то ее можно найти, взяв производную от функции v ( t ), то есть а( t ) = v ′( t ). Однако сама скорость получается при дифференцировании закона движения s ( t ), то есть v ( t ) = s ′( t ). Тогда получается, что

То есть физический смысл второй производной заключается в том, что вторая производная закона движения s ′′( t ) в момент t ₀ равна ускорению тела в этот самый момент.

Далее находим отношение ∆ v / ∆ t :

Получили, что это отношение является постоянной величиной и равно 2. Естественно, что предел постоянной величины равен этой величине:

Напомним, что важнейший закон механики, известный как второй закон Ньютона, выглядит так:

где F – это сила, действующая на тело;

Однако теперь мы знаем, что ускорение является второй производной от закона движения. В связи с этим его можно переписать в виде

И на самом деле в физике значительно чаще используется именно такая его формулировка. Это лишний раз подтверждает значимость понятия производной.

Источник

Как найти тангенс угла наклона прямой

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

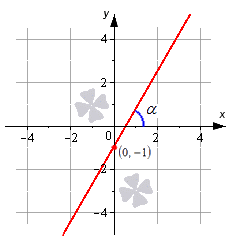
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

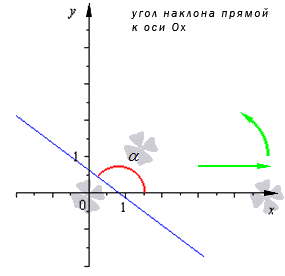
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Уравнение с угловым коэффициентом

Ответ: М 1 принадлежит прямой, а М 2 нет.

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Решение

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Решим задачу обратную данной.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:

— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.

Что такое абсцисса и ордината точки было описано в прошлой статье данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.

Уравнение прямой на координатной плоскости имеет вид:

где k – это и есть угловой коэффициент прямой.

Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.

Он лежит в пределах от 0 до 180 градусов.

То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).

Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.

Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:

Рассмотрим задачи (аналогичные задачам из открытого банка заданий):

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).

В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:

Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

*Оба катета равны шести (это их длины).

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки имеют координаты (5;0) и (0;5). Значит,

Получили, что угловой коэффициент k = – 1.

Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

В данной задаче можно найти уравнение прямой a, определить угловой коэффициент для неё. У прямой b угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b. А затем, подставив в него значение y = 0, найти абсциссу. НО!

В данном случае, проще использовать свойство подобия треугольников.

Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.

Искомая абсцисса равна 40/3.

Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью оx.

Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.

Нам известны точки, через которые проходит прямая а. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:

По условию точки имеют координаты (0;8) и (–12;0). Значит,

Получили, что угловой k = 2/3.

*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.

Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:

Найти величину b мы можем подставив абсциссу и ординату в уравнение:

Таким образом, прямая имеет вид:

Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).

Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).

Формула уравнения прямой походящей через две данные точки имеет вид:

Наши точки имеют координаты (0;0) и (10;24). Значит,

Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:

Значение b найдём подставив в это уравнение координаты точки В(10;12):

Получили уравнение прямой:

Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:

*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).

Искомая ордината равна –12.

Найдите ординату точки пересечения прямой, заданной уравнением

Координата точки пересечения заданной прямой с осью оу имеет вид (0;у). Подставим в уравнение абсциссу х = 0, и найдём ординату:

Ордината точки пересечения прямой с осью оу равна 3.

Найдите ординату точки пересечения прямых, заданных уравнениями

Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:

В первом уравнении подставляем – х вместо у:

Ордината равна минус шести.

Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).

Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).

Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Прямая a проходит через точки с координатами (0;4) и (–6;0). Прямая b проходит через точку с координатами (0; –6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).

Найдите абсциссу точки пересечения прямой, заданной уравнением 2х + 2у = 6, с осью ох.

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3х + 2у = 6 и у = х.

Конечно, некоторые задачи, которые мы рассмотрели можно было решить более рациональными способами. Но ставилась цель показать разные подходы к решению. Надеюсь, это удалось.

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.

2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.

3. Помните о том, что угловые коэффициенты параллельных прямых равны.

4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.

5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.

6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:

>> Угол наклона прямой от 0 до 90 градусов

>> Угол наклона прямой от 90 до 180 градусов

В данных двух случаях, по свойству тангенса :

То есть, чтобы найти уголвой коэффициент прямой, необходимо вычислить тангенс бетта в полученном прямоугольном треугольнике и записать результат с отрицательным знаком.

В данной рубрике продолжим рассматривать задачи, не пропустите!

Функция НАКЛОН в Excel предназначена для определения угла наклона прямой, используемой для аппроксимации данных методом линейной регрессии, и возвращает значение коэффициента a из уравнения y=ax+b. Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).

Фактически, функция НАКЛОН вычисляет значение, которое характеризует скорость изменения данных вдоль линии регрессии. Зная наклон (коэффициент a) и значение коэффициента b можно рассчитать приближенные будущие значения какого-либо свойства y, которое меняется при изменении характеристики x.

Примеры использования функции НАКЛОН в Excel

Для расчета наклона линии регрессии используется уравнение:

Функция НАКЛОН не может быть использована для анализа коллинеарных данных и будет возвращать код ошибки #ДЕЛ/0! в отличие от функции ЛИНЕЙН, которая использует иной алгоритм расчета и возвращает как минимум одно полученное значение.

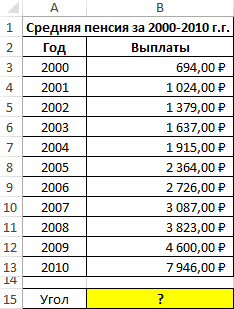
Пример 1. Определить наклон аппроксимирующей прямой для показателей средней пенсии на протяжении нескольких лет.

Вид исходной таблицы данных:

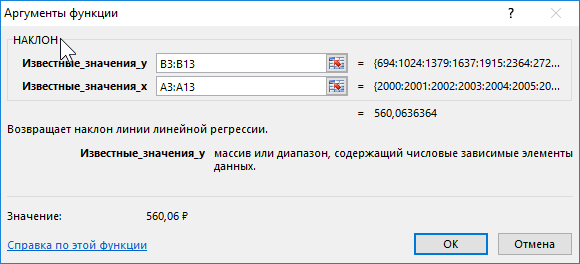
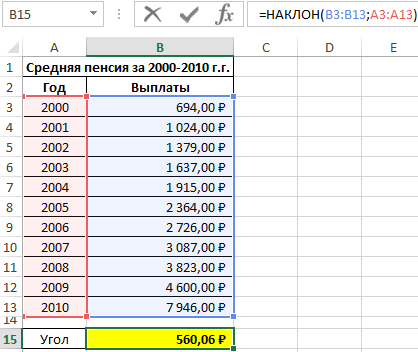
Для нахождения наклона используем следующую формулу:

В результате вычислений получим:

Полученное значение свидетельствует о том, что на протяжении обозначенного периода размер пенсионных выплат в среднем увеличивался примерно на 560 рублей.

Прогноз объема продаж по линейно регрессии в Excel

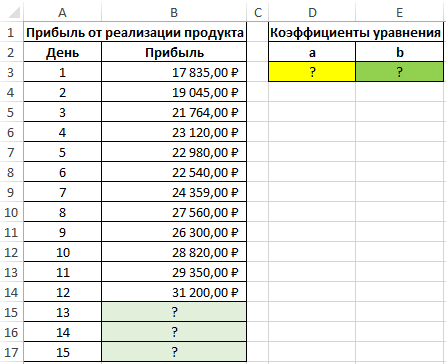
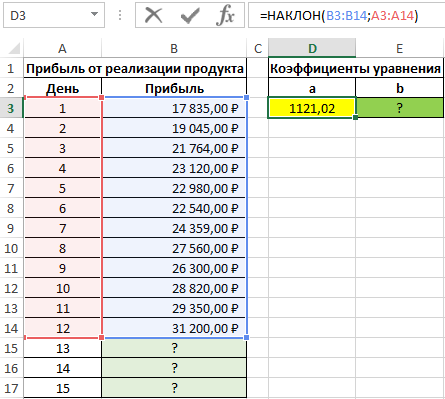
Пример 2. В таблице Excel содержатся данные о прибыли за продажи некоторого продукта компании на протяжении последних нескольких дней. Рассчитать коэффициенты a и b уравнения прямой y=ax+b, аппроксимирующей данные. На основе полученного уравнения спрогнозировать данные о продажах для трех последующих дней.

Вид таблицы с данными:

Для нахождения коэффициента a используем следующую формулу:

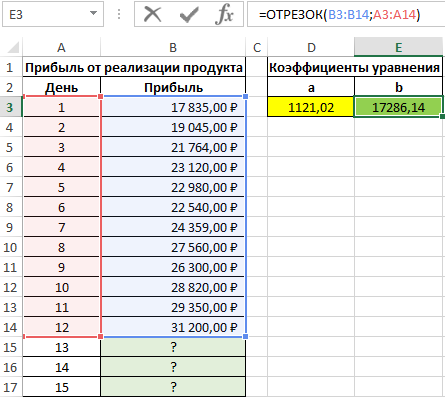
Коэффициент b рассчитывается с помощью следующей функции:

Искомое уравнение имеет вид:

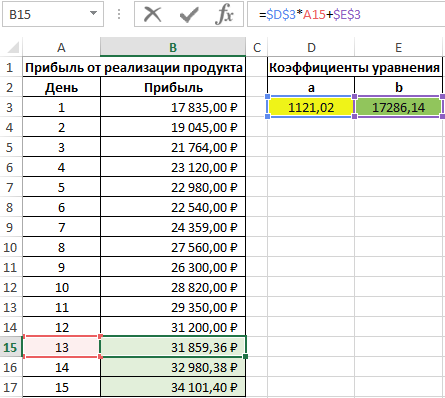
Для определения последующих значений y достаточно лишь подставить требуемое значение x. Выполним расчет предполагаемой прибыли для 13-го дня:

Используем функцию автозаполнения чтобы получить значения для остальных дней:

Анализ корреляции спроса и объема производства в Excel

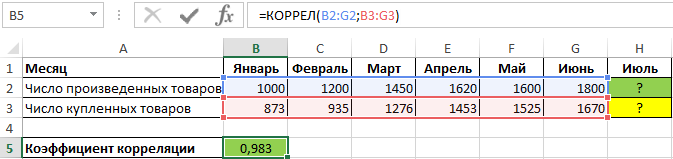
Пример 3. В таблице содержатся данные о количестве произведенной продукции за месяц, а также о числе приобретенных товаров данной марки покупателями. Отобразить взаимосвязь между данными графически, определить, целесообразно ли использовать уравнение линейно регрессии для описания корреляции между спросом и числом произведенных товаров.

Вид таблицы данных:

Для определения зависимости между двумя рядами числовых данных рассчитаем коэффициент корреляции по формуле:

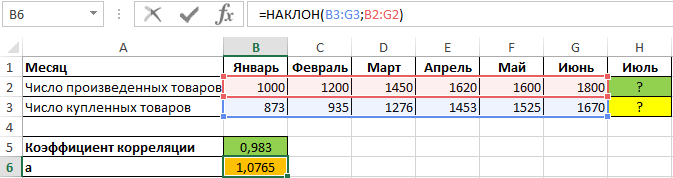
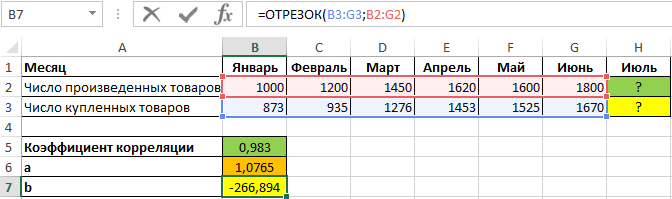
Полученное значение (0,983) свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Поэтому целесообразно использовать аппроксимирующую прямую, для нахождения коэффициентов уравнения которой используем формулы:

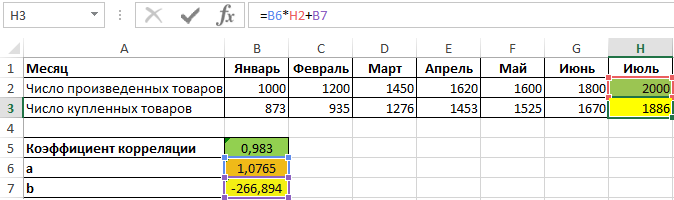
Для нахождения спроса на товары за июль при условии, что будет произведено, например, 2000 единиц продукции, используем полученное уравнение:

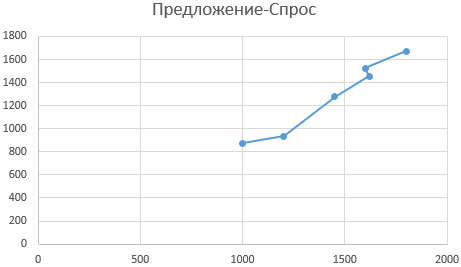
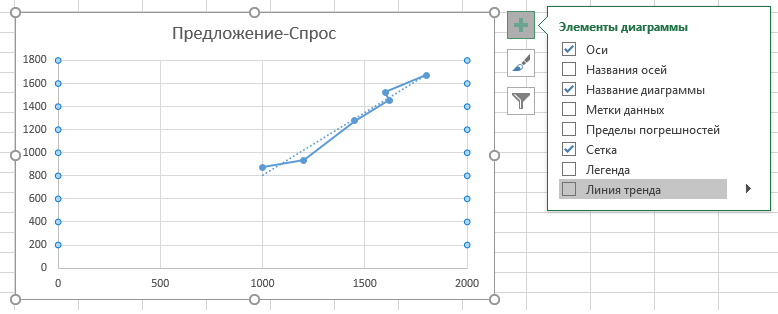
Альтернативным использованию функции НАКЛОН вариантом нахождения наклона в Excel является графический метод. Построим график на основе имеющихся данных, при этом для значений X выберем диапазон ячеек со значениями числа произведенных товаров, а для Y – с числом купленных товаров:

Отобразим на графике линию тренда:

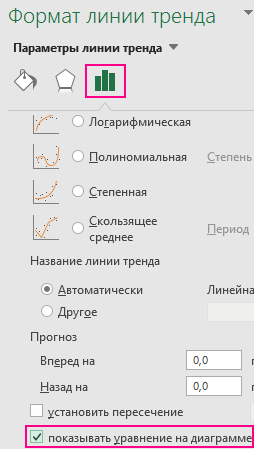
В меню «Формат линии тренда» установим флажок напротив пункта «показывать уравнение на диаграмме»:

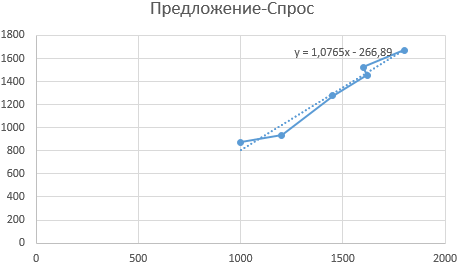
График примет следующий вид:

Как видно, найденные коэффициенты a и b соответствуют отображаемым на графике.

Особенности использования функции НАКЛОН в Excel

Функция имеет следующий синтаксис:

Описание аргументов (все являются обязательными для заполнения):

Источник