Сделать выборку что это значит
Значение слова «выборка»
1. Действие по глаг. выбрать—выбирать (в 4 знач.). Выборка грунта. Выборка сети. □ Клава Гусева работала в этот день вблизи шлюза на выборке земли. Паустовский, Героический юго-восток.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Качественная характеристика выборки — что именно мы выбираем и какие способы построения выборки мы для этого используем.
Количественная характеристика выборки — сколько случаев выбираем, другими словами объём выборки.
Объект исследования очень обширный. Например, потребители продукции глобальной компании — огромное количество территориально разбросанных рынков.
Существует необходимость в сборе первичной информации.
ВЫ’БОРКА, и, ж. 1. только ед. Действие по глаг. выбирать в 4 и 5 знач. — выбрать. Произвести выборку. Сделать выборку. Проверить документы на выборку (т. е. не все подряд, а только нек-рые, отобранные). 2. чаще мн. Выписка, выбранное место из книги (разг. устар.). Рукопись заключала в себе выборки из писателей. 3. только ед. Действие по глаг. выбирать в 7 знач. — выбрать (стол.). В. рубанком. 4. Углубление, выбранное столярным инструментом (стол.). Глубокие выборки.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
вы́борка
1. действие по значению гл. выбирать, выбрать ◆ При глубокой выборке или при гравировании закруглений применяют болштихель или аналогичной формы зубило. Александр Навроцкий, «Ковка и художественная отделка кованых изделий», 2016 г.
2. результат такого действия; группа однородных предметов, отобранных из серии (обычно для проверки их качества)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова мириада (существительное):
Выборка
Выборка или выборочная совокупность — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.
Содержание
Объём выборки
Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.
Зависимые и независимые выборки
При сравнении двух (и более) выборок важным параметром является их зависимость. Если можно установить гомоморфную пару (то есть, когда одному случаю из выборки X соответствует один и только один случай из выборки Y и наоборот) для каждого случая в двух выборках (и это основание взаимосвязи является важным для измеряемого на выборках признака), такие выборки называются зависимыми. Примеры зависимых выборок:
В случае, если такая взаимосвязь между выборками отсутствует, то эти выборки считаются независимыми, например:
Соответственно, зависимые выборки всегда имеют одинаковый объём, а объём независимых может отличаться.
Сравнение выборок производится с помощью различных статистических критериев:
Репрезентативность
Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.
Пример нерепрезентативной выборки
На действительных же выборах, как известно, победил Рузвельт, набрав более 60 % голосов. Ошибка «Литрери Дайджест» заключалась в следующем: желая увеличить репрезентативность выборки, — так как им было известно, что большинство их подписчиков считают себя республиканцами, — они расширили выборку за счёт людей, выбранных из телефонных книг и регистрационных списков. Однако они не учли современных им реалий и в действительности набрали ещё больше республиканцев: во время Великой депрессии обладать телефонами и автомобилями могли себе позволить в основном представители среднего и высшего класса (то есть большинство республиканцев, а не демократов).
Виды плана построения групп из выборок
Выделяют несколько основных видов плана построения групп [2] :
Типы выборки
Выборки делятся на два типа:
Вероятностные выборки
Процедура построения простой случайной выборки включает в себя следующие шаги:
1. необходимо получить полный список членов генеральной совокупности и пронумеровать этот список. Такой список, напомним, называется основой выборки;
2. определить предполагаемый объем выборки, то есть ожидаемое число опрошенных;
3. извлечь из таблицы случайных чисел столько чисел, сколько нам требуется выборочных единиц. Если в выборке должно оказаться 100 человек, из таблицы берут 100 случайных чисел. Эти случайные числа могут генерироваться компьютерной программой.
4. выбрать из списка-основы те наблюдения, номера которых соответствуют выписанным случайным числам
1. зачастую сложно создать основу выборочногo наблюдения, которая позволила бы провести простую случайную выборку.
2. результатом применения простой случайной выборки может стать большая совокупность, либо совокупность, распределенная по большой географической территории, что значительно увеличивает время и стоимость сбора данных.
3. результаты применения простой случайной выборки часто характеризуются низкой точностью и большей стандартной ошибкой, чем результаты применения других вероятностных методов.
4. в результате применения SRS может сформироваться нерепрезентативная выборка. Хотя выборки, полученные простым случайным отбором, в среднем адекватно представляют генеральную совокупность, некоторые из них крайне некорректно представляют изучаемую совокупность. Вероятность этого особенно велика при небольшом объеме выборки.
Невероятностные выборки
Отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям – доступности, типичности, равного представительства и т.д.
6.Модальная выборка. 7.экспертная выборка. 8.Гетерогенная выборка.
Стратегии построения групп
Рандомизация
Рандомизация, или случайный отбор, используется для создания простых случайных выборок. Использование такой выборки основывается на предположении, что каждый член популяции с равной вероятностью может попасть в выборку. Например, чтобы сделать случайную выборку из 100 студентов вуза, можно сложить бумажки с именами всех студентов вуза в шляпу, а затем достать из неё 100 бумажек — это будет случайным отбором (Гудвин Дж., с. 147).
Попарный отбор
Попарный отбор — стратегия построения групп выборки, при котором группы испытуемых составляются из субъектов, эквивалентных по значимым для эксперимента побочным параметрам. Данная стратегия эффективна для экспериментов с использованием экспериментальных и контрольных групп с лучшим вариантом — привлечением близнецовых пар (моно- и дизиготных), так как позволяет создать.
Стратометрический отбор
Стратометрический отбор — рандомизация с выделением страт (или кластеров). При данном способе формирования выборки генеральная совокупность делится на группы (страты), обладающие определёнными характеристиками (пол, возраст, политические предпочтения, образование, уровень доходов и др.), и отбираются испытуемые с соответствующими характеристиками.
Приближённое моделирование
Приближённое моделирование — составление ограниченных выборок и обобщение выводов об этой выборке на более широкую популяцию. Например, при участии в исследовании студентов 2-го курса университета, данные этого исследования распространяются на «людей в возрасте от 17 до 21 года». Допустимость подобных обобщений крайне ограничена.
Приближенное моделирование – формирование модели, которая для четко оговоренного класса систем (процессов) описывает его поведение (или нужные явления) с приемлемой точностью.
Примечания
Литература
Наследов А. Д. Математические методы психологического исследования. — СПб.: Речь, 2004.
Часто бывает так, что необходимо проанализировать какое-либо конкретное социальное явление и получить информацию о нем. Такие задания часто возникают в статистике и при статистических исследованиях. Проверить полностью определенное социальное явление чаще всего бывает невозможным. Например, как узнать мнение населения или всех жителей определенного города по какому-либо вопросу? Спрашивать абсолютно всех – дело практически невозможное и очень трудоемкое. В таких случаях нам и необходима выборка. Это именно то понятие, на котором основаны практически все исследования и анализы.
Что такое выборка
При анализе конкретного социального явления необходимо получить информацию о нем. Если взять любое исследование, то можно заметить, что исследованию и анализу подлежит не каждая единица совокупности объекта исследования. Во внимание берется только определенная часть всей этой совокупности. Вот этот процесс и является выборкой: когда исследуются только определенные единицы из множества.
Конечно же, многое зависит от вида выборки. Но есть и основные правила. Главное из них гласит, что отбор из совокупности должен быть абсолютно случайным. Единицы совокупности, которые будут использованы, не должны быть выбраны из-за какого-либо критерия. Грубо говоря, если необходимо набрать совокупность из населения определенного города и отобрать только мужчин, то в исследовании будет ошибка, потому что отбор был проведен не случайно, а отобран по гендерному признаку. Практически все методы выборки основаны на этом правиле.
Правила выборки
Для того чтобы отобранная совокупность отражала основные качества всего явления, она должна быть построена по конкретным законам, где основное внимание необходимо уделять следующим категориям:
Особенности выборочного наблюдения и составления выборки заключаются в следующем:
Выборочное наблюдение
Но выборочное наблюдение может использоваться только в тех случаях, когда необходимо исследовать лишь малую группу единиц. Например, при исследовании соотношения мужчин к женщинам в мире, будет использоваться выборочное наблюдение. По понятным причинам – взять во внимание каждого жителя нашей планеты невозможно.
Выборочная и генеральная совокупность
На самом деле все не так сложно, как звучит. В любом объекте изучения есть две системы: генеральная и выборочная совокупность. Что же это такое? Все единицы относятся к генеральной. А к выборочной – те единицы общей совокупности, которые были взяты для выборки. Если все правильно сделано, то отобранная часть будет составлять уменьшенный макет всей (генеральной) совокупности.
Если говорить о генеральной совокупности, то можно выделить всего две ее разновидности: определенная и неопределенная генеральная совокупность. Зависит от того, известно ли общее количество единиц данной системы или нет. Если это определенная генеральная совокупность, то выборку будет делать легче из-за того, что известно, какой процент от общего количества единиц будет составлять выборка.
Этот момент очень необходим в исследованиях. Например, если необходимо исследовать процент недоброкачественной продукции кондитерских изделий на конкретном заводе. Допустим, что генеральная совокупность уже определена. Точно известно, что в год это предприятие производит 1000 кондитерских изделий. Если сделать выборку 100 случайных кондитерских изделий из этой тысячи и отправить их на экспертизу, то погрешность будет минимальной. Грубо говоря, исследованию подлежало 10 % всей продукции, и по результатам можем, приняв во внимание ошибку репрезентативности, говорить о недоброкачественности всей продукции.
А если провести выборку 100 кондитерских изделий из неопределенной генеральной совокупности, где их на самом деле было, допустим, 1 млн единиц, то результат выборки и самого исследования будет критически неправдоподобным и неточным. Чувствуете разницу? Поэтому определенность генеральной совокупности в большинстве случаев крайне важна и очень сильно влияет на результат исследования.
Репрезентативность совокупности
Иными словами, если после отбора часть сохраняет те же самые тенденции и особенности что и все количество исследуемого, то такая совокупность называется репрезентативной. Но не каждая определенная выборка может быть отобрана из репрезентативной совокупности. Бывают и такие объекты исследования, выборка которых просто не может быть репрезентативной. Отсюда и возникает понятие ошибки репрезентативности. Но об этом поговорим подробнее чуть больше.
Как сделать выборку
Итак, чтобы репрезентативность была максимальной, выделяют три основные правила выборки:
Погрешность (ошибка) репрезентативности
Главной характеристикой качества выбранной выборки является понятие «погрешности репрезентативности». Что же это такое? Это определенные расхождения между показателями выборочного и сплошного наблюдения. По показателям погрешности репрезентативность делят на надежную, обычную и приближенную. Иначе говоря, допустимыми являются отклонения в размере до 3 %, от 3 до 10 % и от 10 до 20 % соответственно. Хотя в статистике желательно, чтобы погрешность не превышал 5-6 %. В противном случае есть повод говорить о недостаточной репрезентативности выборки. Для вычисления погрешности репрезентативности и того, как она влияет на выборочную или генеральную совокупность, во внимание берутся многие факторы:
В конкретно заданных исследованиях процент погрешности среднего значения обычно задается самим исследователем на основании программы наблюдения и согласно данным ранее проведенных исследований. Как правило, считается допустимой предельная ошибка выборки (ошибка репрезентативности) в пределах 3-5 %.
Больше – не всегда лучше
В то же время нельзя и чрезмерно увеличивать размер погрешности репрезентативности. Ведь в этом случае, хотя и произойдет уменьшение объема выборочной совокупности, это приведет к ухудшению достоверности полученных результатов.
Какие вопросы обычно ставится перед исследователем
Любое исследование если и проводится, то для какой-то цели и для получения каких-то результатов. При проведении выборочного исследования, как правило, ставятся начальные вопросы:
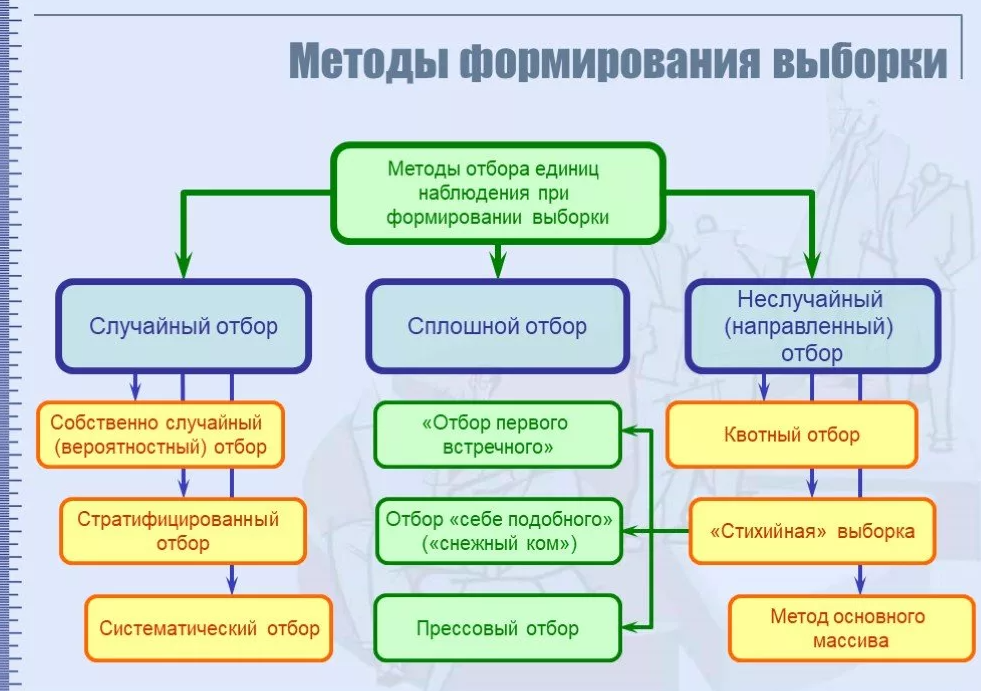
Способы отбора единиц исследования в выборку
Не каждая выборка является репрезентативной. Иногда один и тот же признак по-разному выражен в целом и в ее части. Для достижения требований репрезентативности целесообразным является использование различных приемов создания выборки. Причем использование того или иного способа зависит от конкретных обстоятельств. Среди таких приемов создания выборки выделяют:
Случайный отбор представляет собой систему мероприятий, направленных на случайный отбор единиц совокупности, когда вероятность попасть в выборку является равной для всех единиц генеральной совокупности. Этот прием целесообразно применять только в случае однородности и небольшого количества присущих ей признаков. В противном случае некоторые характерные черты рискуют быть не отраженным в выборке. Признаки случайного отбора лежат в основе всех других способов построения выборки.
При механическом отбор единиц проводится через определенный интервал. Если необходимо сформировать выборку конкретных преступлений, можно изымать из всех карточек статистического учета зарегистрированных преступлений каждую 5-ю, 10-ю или 15-ю карточку в зависимости от их общего количества и имеющихся размеров выборки. Недостатком этого способа является то, что перед отбором необходимо иметь полный учет единиц совокупности, затем нужно провести ранжирование и только после этого можно проводить выборку с определенным интервалом. Этот метод занимает много времени, поэтому он и не часто используется.
Типичный (районированный) отбор – вид выборки, при котором генеральную совокупность разделяют на однородные группы по определенному признаку. Иногда исследователи употребляют вместо «групп» другие термины: «районы» и «зоны». Затем из каждой группы в случайном порядке отбирается определенное количество единиц пропорционально удельному весу группы в общей совокупности. Типичный отбор часто осуществляется в несколько этапов.
Понятие и практическое применение выборки в математической статистике
Каждое исследование по-своему уникально. Автор научной работы самостоятельно определяет приемы, методики анализа, исходя из имеющихся у него на руках данных. В большинстве случаев ученые прибегают к двум ключевым приемам: научный анализ данных, используемый в теоретических проектах, и математико-экономические приемы для определения динамики, силы воздействия факторов на результат. В любом случае им на помощь приходят методы математической статистики, под которой понимают раздел математики, позволяющий грамотно классифицировать первоначальные данные, проанализировать их, смоделировать ситуацию и спрогнозировать потенциальный результат в зависимости от набора факторов и обстоятельств.
Каждое исследование по-своему уникально. Автор научной работы самостоятельно определяет приемы, методики анализа, исходя из имеющихся у него на руках данных. В большинстве случаев ученые прибегают к двум ключевым приемам: научный анализ данных, используемый в теоретических проектах, и математико-экономические приемы для определения динамики, силы воздействия факторов на результат. В любом случае им на помощь приходят методы математической статистики, под которой понимают раздел математики, позволяющий грамотно классифицировать первоначальные данные, проанализировать их, смоделировать ситуацию и спрогнозировать потенциальный результат в зависимости от набора факторов и обстоятельств.
В каждом исследовании независимо от того, к какой области наук оно относится, автор научного изыскания должен выделить объект и факторы, оказывающие на него воздействие. Притом он оценивает влияние каждого отдельного и совокупное воздействие критериев на результат. То есть фактически исследователь изначально вводит некие ограничения по количеству изучаемых объектов, группы факторов, которые он принимает во внимание и пр. Это значит, что в большинстве случае исследователь исследует конкретную выборку.
Что это такое?
Математическая статистика – это удачное сочетание точных наук с неточными, практических и теоретических наблюдений, закономерностей и пр. Данная наука позволяет грамотно систематизировать данные, представить их в удобной для анализа форме.
Методы математической статистики предполагают, что исследователь ограничивает свое научное изыскание конкретными фактами в зависимости от цели проведения запланированных мероприятий. В этом случае целесообразно применять понятие выборки, под которой понимают совокупность объектов и факторов, воздействующих на них, с целью определения взаимосвязи, степени влияния и потенциальных результатов.

Выборка – это некая часть из общей совокупности элементов. Если исследователь тщательно планирует исследование, определяет условия его проведения, действующие ограничения и пр., то полученные результаты в дальнейшем можно перенести на генеральную совокупность. То есть изучение выборок позволяет сделать сначала частный вывод, а затем, оценив выборку на репрезентативность, сделать общий вывод в отношении большего числа факторов и объектов.
Нужна помощь преподавателя?
Мы всегда рады Вам помочь!
Таким образом, математическая статистика позволяет установить частные и общие тенденции на основе выборок. Главное, наметить цель исследования, обозначить необходимые условия проведения, выделить объект и воздействующие на него критерии (факторы), подобрать методы и инструменты.
Какие выборки бывают?
В любой науке существуют свои нюансы, но при проведении исследования важно понимать, что автору предстоит разобраться в конкретной ситуации, выделить ключевые параметры и данные которыми он обладает. Уже на данном этапе происходит выделение из генеральной (общей) совокупности явлений и процессов определенных элементов (выборки), удовлетворяющих конкретным условиям (цели, методологии исследования и пр.).

Поэтому в математической статистике принято выделять генеральную и выборочную совокупность. Генеральная совокупность — это пространство, совокупность элементов, среди которых автор будет выбирать интересующие или подходящие для его исследования элементы. Выборочная совокупность представляет собой те элементы, которые удовлетворяют заявленным исследователем критериям.
Например, автор научной работы намерен изучить геометрические фигуры. Это будет генеральная совокупность. Но в исследовании ему нужно определить диагонали тех фигур, которые имеют 4 стороны и только прямые углы, то есть квадраты и прямоугольники. Это уже будет выборочная совокупность.
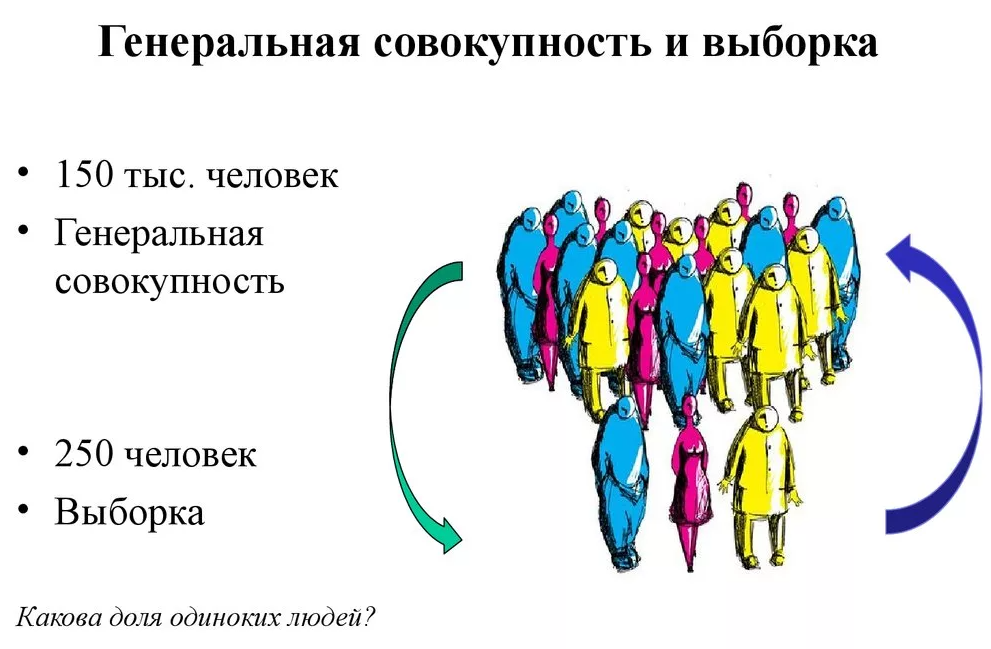
Также примером генеральной совокупности могут быть люди. В исследовании же автор может анализировать их в зависимости от возраста, пола, образования или опыта работы, места проживания и пр. В этом случае производится выборка в зависимости от определенного критерия.
В математической статистике также принято выделять такое понятие, как объем выборки – это количество элементов выборки, то есть число испытуемых. Например, объем выборки генеральной (общей) совокупности N может составлять 1000, а выборочной совокупности (которые удовлетворяют определенным условиям и требованиям) n – 100.
Правила выделения и анализа выборки
Для того чтобы результаты исследования были достоверными, качественными и репрезентативными, исследователю необходимо пройти ряд этапов:
Здесь целесообразно понять: что будет изучаться, какими способами, для чего необходимо исследование, какие действия необходимо предпринять и пр. Также необходимо определить общую совокупность изучаемых явлений, методологию.
Автор важно понимать, какие ограничения будут действовать: какие характеристики свойственные объекту, чем будет ограничиваться его исследование (каким научным полем или областью). Для этого вводится система ограничений для объекта в виде предмета и по иным характеристиками: возраст количество, личные или профессиональные качества, поведение, зависимости и пр.
Также на данном этапе выделяются те факторы, которые оказываю на объект воздействие или те параметры, воздействие которых предстоит оценить.
Анализ предполагает определение вида выборки, наличия зависимости между переменными (факторами) и объектом, способы оценки влияния на результат, прогнозирование результатов и пр. На этой стадии следует зафиксировать текущее состояние объекта и факторов, провести эксперимент или наблюдение, моделирование ситуации и пр., зафиксировать все изменения и полученные результаты, а затем интерпретировать их удобным способом: таблица и расчеты, график, схема, диаграмма, чертеж и пр.
После проведения всех операций над выборкой исследователь должен понять, репрезентативна она или нет, а также сформулировать окончательный частный, а затем общий вывод. Частное умозаключение будет отобрать тенденции в отношении и выборочной совокупности, а общий – в целом по проделанной работе или по генеральной совокупности (если выборка представительна).
Таким образом, выборка выступает основой любого исследования, так как позволяет исследовать конкретную проблему, объект, понять принцип действия отдельных законов и правил, оценить влияние отдельных параметров на конкретный показатель или результат, оптимизировать ситуацию. Главное грамотно подбирать элементы выборки, умело их анализировать, производить необходимые действия и получать достоверные результаты.
Трудности с учебой?
Помощь в написании студенческих и
аспирантских работ!