Шарп в трейдинге что такое
Коэффициент Шарпа
Коэффициент Шарпа, как и альфа, оценивает труд управляющего. Только сравнивает доходность портфеля не с движением какого-либо эталона, а с колебанием доходности самого портфеля за анализируемый период. Т.е. дается «внутренняя» оценка «качества» доходности портфеля, без использования «внешних» данных. Другими словами, дается абсолютная, а не относительная оценка полученной за период доходности.
• R — доходность портфеля (актива)
• Rf — доходность от альтернативного вложения
• σ — стандартное отклонение доходности портфеля (актива)
Колебания доходности — это риск. Высокие колебания — это высокий риск, и они должны приносить высокий доход. Колебания доходности измеряются стандартным отклонением, которое помещается в знаменатель дроби, рассчитывающей коэффициент Шарпа. В числителе дроби – доходность портфеля, очищенная от гарантированной рыночной доходности — от доходности безрискового вложения, в качестве которого, как правило, берется депозит в Сбербанке.
Если портфель показал доходность 30% со стандартным отклонением равным 10, а депозит Сбербанка принес бы 12%, то коэффициент Шарпа будет равен (30-12)/10 = 1,8. Можно сказать, что за каждую единицу риска были получены 1,8 единиц доходности сверх гарантированной безрисковой доходности.
Чем значение коэффициента Шарпа выше, тем выгоднее управляющий использует риск портфеля. Причем, благодаря тому, что этот коэффициент использует стандартное отклонение доходности самого портфеля, а не внешний эталон, он может быть применен для сравнения между собой различный портфелей.
При одинаковой доходности портфели могут иметь разные значения этого коэффициента, потому что они принимают на себя разное количество риска. Портфель, у которого коэффициент Шарпа выше при одинаковой доходности, достиг результата с меньшим риском. Чем выше стандартное отклонение, тем больше знаменатель уравнения коэффициента Шарпа, а значит портфелю нужно показывать высокую доходность, чтобы заработать высокое значение этого показателя. Портфелю с низким уровнем риска (небольшим стандартным отклонением) достаточно показывать умеренную доходность, чтобы его коэффициент Шарпа был достаточно высоким.
У коэффициента Шарпа есть преимущество перед альфой. Стандартное отклонение измеряет волатильность фонда в абсолютной величине, а не относительной, как альфа. Поэтому, если для полезности альфы должен быть высоким коэффициент корреляции, то коэффициент Шарпа всегда имеет полноценное значение, независимо от других показателей.
Что такое Коэффициент Шарпа – Примеры использования, Нормы значений
Как начать торговать на бирже: Инструкции и Примеры, Обучение
Какие значения должен показывать Коэффициент Шарпа (Sharp Ratio), чего хотел добиться Уильям Шарп и как применять коэффициент на Форекс или фондовом рынке.
В инвестиционной деятельности важна не только конечная доходность, но и риск. Нужна оценка эффективности, показатель, позволяющий понять окупается ли принятый инвестором риск. В роли такого показателя выступает коэффициент Шарпа, он был разработан в 1966 году, но за прошедшие десятилетия не утратил актуальности.
Ниже – разбор логики этого показателя, а также примеры расчетов на Форекс и фондовом рынке.
Что такое коэффициент Шарпа (простыми словами)
Коэффициент Шарпа – это мера рентабельности инвестиционной стратегии. С его помощью оценивается награда за принимаемый инвестором риск. В расчетную формулу закладывается и так называемый безрисковый доход, обычно в его роли выступают проценты по банковскому депозиту.
Коэффициент Шарпа простыми словами – это показатель того, окупается ли риск. Он универсален, подходит и для оценки Форекс-стратегий, и для изучения надежности долгосрочного инвестирования в ценные бумаги различных компаний.
Этот коэффициент не ранжирует стратегии по доходности, производится более глубокая оценка. Важна стабильность получения дохода, поэтому с точки зрения методики Шарпа предпочтительнее может оказаться стратегий с более низким, но стабильным профитом по сравнению с высокодоходным, но нестабильным результатом.
История метода Уильяма Шарпа
Уильям Шарп (William Sharpe) посвятил всю жизнь экономике, он концентрировал внимание на вопросах оценки инвестиций, заложил основы современной теории цен на финансовых рынках, особое внимание уделял равновесию на рынках капитала. Исследовательскую работу он совмещал с преподаванием в университетах Стэнфорда, Ирвина, привлекался к работе над планированием инвестиционной политики пенсионных/страховых фондов.

В 1990 году Шарп совместно с Гарри Марковицем (Harry Markowitz) и Мертоном Миллером (Merton Miller) получил Нобелевскую премию в области экономики.
Сам Шарп не называл коэффициент своим именем, в 1966 году он получил название «Reward to Variability Ratio». На русский язык это можно перевести как коэффициент «доходность-разброс». Расчет коэффициента Шарпа не изменился с 1966 года, а современное название этот показатель получил после всемирного признания его методики.
Получение Шарпом Нобелевской премии окончательно укрепило разработанную им методику в качестве негласного стандарта при оценке инвестиций. Такая оценка проводилась и до появления этого показателя, но не существовало простой универсальной формулы.
Этим и выделяется работа Шарпа – сложную теорию он превратил в простейшую математическую зависимость, применимую для оценки любых инвестиций.
Формула коэффициента Шарпа выглядит так:
Приняты следующие обозначения:
Из формулы видно, что с ростом нестабильности доходности увеличивается знаменатель дроби. Это объясняет причину, по которой нестабильные инвестиционные портфели обладают невысоким Sharp Ratio.
Как использовать коэффициент Шарпа при инвестициях или торговле на бирже
Инвестиции и активный трейдинг – разные методы работы с точки зрения действий инвестора/трейдера.
Несколько отличается и применение методики Шарпа:
Полученное после расчетов число может использоваться и само по себе, для оценки окупаемости риска, так и для выбора лучшего варианта инвестирования из нескольких.
Какие должны быть значения коэффициента Шарпа – нормы
В зависимости от показателей инвестиционной стратегии Sharp Ratio может принимать любые значения, в том числе и отрицательные. При оценке исходят из следующих соображений:
Для наглядности ниже выполнен ручной расчет с использованием Excel. SR рассчитан и для отдельной торговой стратегии для работы на рынке Форекс, и для простого инвестиционного портфеля, состоящего из акций компаний.
Инвестпортфель состоит из бумаг Apple, Amazon и AMD, для расчетов загружались данные от Just2Trade. Доля бумаг – 30%, 30% и 40% соответственно.
Ручной расчет проводится по следующей схеме:
Коэффициент Шарпа при таких исходных данных равен -2,37, инвестпортфель нежизнеспособен, на этой дистанции банковский депозит дал бы больший эффект. Это объясняется тем, что для анализа выбран непродолжительный период истории, во время падения американского рынка. Если оценивается полноценный инвестиционный портфель, то анализ проводится на более длинной дистанции.
Этот пример расчетов на фондовом рынке – не единственный вариант использования коэффициента Шарпа. По той же методике можно оценивать, например, работу управляющих ПИФами и ETF фондами. Принцип тот же, меняются лишь исходные данные.
Тот же подход сохраняется и при анализе Форекс-стратегий. Отличие заключается в том, что в случае с Форексом безрисковая доходность приравнивается к нулю. За счет этого завышается коэффициент Шарпа.
Простейший пример расчета:
Другая торговая система дает меньший доход в процентах, но результат более стабилен:
Если сравнивать стратегии по доходности, то первая система кажется более выгодной. Средняя прибыль в сделке 7%, а по второй – всего 3%. Но в первой ТС слишком нестабильны результаты, в одной сделке трейдер может заработать 12%, в другой – потерять деньги. Вторая система стабильнее и волатильность доходности в разы ниже.
Именно поэтому с точки зрения методики Шарпа выбрать стоило бы вторую стратегию.
В примерах для расчетов использовано всего 7 сделок. В реальных расчетах берется массив статистики с сотнями и тысячами сделок. Чем больше дистанция, на которой проводится анализ, тем более приближен к реальности результат расчетов.
Автоматический расчет коэффициента Шарпа
Ручной расчет Sharp Ratio возможен, но есть способы облегчить задачу:
Есть и пользовательские калькуляторы, ими периодически делятся на профильных форумах, но нет гарантий, что автор будет поддерживать такую программу в течении продолжительного времени. Перед использованием таких инструментов желательно проверить их эффективность ручным расчетом. Вопрос, как посчитать Sharpe Ratio разбирался выше.
Что такое безрисковая прибыль
Безрисковый доход – доход, который инвестор может получить с нулевым риском. Понятие в некоторой степени условное, так как даже при инвестировании в ОФЗ или корпоративные облигации сохраняется вероятность неисполнения эмитентом своих обязательств в случае банкротства.
В зависимости от направления работы безрисковый доход принимается разным:
Выше говорилось, что Sharp Ratio – оценка окупаемости риска инвестиций. Если риск не окупается, то с точки зрения надежности получения дохода выгоднее вложиться в безрисковое направление с меньшей доходностью.
Как измеряется доходность
В инвестировании есть целый набор разных типов доходностей. Инвесторы оперируют такими терминами как дивидендная, процентная, годовая, текущая доходность, для облигаций применяется термин доходность к погашению.
В случае с расчетом коэффициента Шарпа в качестве исходных данных может выступать:
Строгих требований к формату исходных данных нет, но желательно, чтобы они были нормально распределены. Если распределение будет с явно выраженной асимметрией, будут наблюдаться искажения оценки с помощью Sharp Ratio.
Что касается подсчета доходности, то методика стандартная. Например, в конце текущего месяца оценивается стоимость портфеля, из нее вычитается стоимость портфеля в конце предыдущего месяца. Полученная разница делится на стоимость портфеля в конце предыдущего месяца и умножается на 100%.
Отклонение
Для многих случайных значений можно рассчитать математическое ожидание или среднее значение. Стандартное отклонение показывает насколько случайная величина отличается от математического ожидания. Чем оно выше, тем выше и волатильность доходности.
Расчет отклонения выполняется в несколько этапов:
Ручной расчет показан лишь для наглядности. То же число можно получить с помощью Excel, в нем есть встроенная функция СТАНДОТКЛОН. Достаточно ввести выбору в таблицу, выбрать функцию и указать диапазон, для которого будет рассчитан показатель стандартного отклонения:
Коэффициент Шарпа в ПАММ-счетах на Альпари
Для удобства сравнения ПАММов в рейтинге Альпари автоматически рассчитывается серия коэффициентов. Sharp Ratio определяется как отношение среднего дохода за день к волатильности доходности. Это позволяет оценить окупаемость риска и выбрать более надежные ПАММы.
В расчете не учитывается безрисковая доходность в виде банковского депозита или годового купона по облигациям. Из-за этого SR несколько завышается, но так как для всех ПАММов он рассчитывается по одной методике, то по нему можно сравнивать эффективность работы управляющих.
Информация по коэффициенту Шарпа находится в разделе «Торговля» в детальной информации о ПАММе. Там же рассчитывается еще несколько показателей:
Коэффициент Сортино – похож на SR, но при расчете учитывается так называемая скорректированная волатильность доходности. Под ней понимается волатильность доходности, полученная только за счет убыточных сделок/отчетных периодов, прибыльные на результат не влияют.
Коэффициент Швагера – показатель того как соотносится усредненная доходность и просадка.
Коэффициент Кальмара – характеризует компенсацию максимальной просадки за счет доходности.
Коэффициент Шарпа – лишь один из этапов анализа ПАММа. При выборе нужно учитывать и тип стратегии, и форму кривой роста депозита, и статистические показатели торговли.
Недостатки
Sharp Ratio – неидеальный показатель, при определенных условиях он может вводить инвестора в заблуждение. К его недостаткам относят:
Эти недостатки некритичны и не снижают ценность Sharp Ratio. Но знать об этих особенностях нужно, чтобы трезво оценивать инвестпортфели/результаты торговли.
Важные выводы
Одна из серьезнейших ошибок инвестора – игнорирование волатильности доходности при оценке инвестпортфелей. Это относится и к трейдерам, оценивающим торговые стратегии. Коэффициент Шарпа позволяет оценить одну из ключевых характеристик – окупаемость принимаемого при инвестировании риска. При долгосрочном инвестировании SR особенно важен.
При использовании Sharpe Ratio нужно понимать природу этого инструмента. Он действительно учитывает волатильность доходности, но высокий SR не означает, что выбранный портфель даст максимальную доходность. SR – это скорее мера стабильности. Если SR > 1,0, то инвестпортфель с высокой вероятностью даст доход, но вряд ли он будет рекордным.
При оценке инвестиций нужен комплексный анализ, SR – лишь одна из характеристик и не может выступать в роли единственного критерия для принятия решения.
Коэффициент Шарпа – оцениваем эффективность вашей стратегии
Добрейшего времени суток, товарищи Форекс трейдеры! Чаще при оценке стратегий на Forex трейдеры смотрят на доходность в процентах. Чем их больше – тем лучше, не так ли? Но % доходности сильно зависит от риска и не отражает эффективности системы. Так какой показатель использовать? Стандартом у финансовых аналитиков считается Коэффициент Шарпа, выведенный нобелевским лауреатом Уильямом Шарпом.
Ниже мы рассмотрим как рассчитать коэффициент Шарпа для оценки эффективности стратегии, разберемся что же он означает (многие умеют его считать, но не понимают его смысла), а также сделаем выводы о том в каких случаях он полезен, а в каких нет.
Коэффициент Шарпа на Форекс
Коэффициент Шарпа придумал известный американский экономист – Уильям Шарп. На сегодня, это один из наиболее часто используемых показателей отношения риска к доходности. Еще большую значимость коэффициент приобрел, когда в 1990 году, за свою модель оценки финансовых активов (CAPM) Шарп был избран лауреатом Нобелевской премии.
Человеку из сферы финансов будет не сложно понять принцип расчета коэффициента Шарпа и что тот должен отображать. По сути, задача сводится к тому, чтобы узнать, сколько избыточной доходности вы получите в связи с удержанием более рискового актива. Думаю, не секрет, что лишний риск всегда должен сполна компенcироваться соответствующей доходностью. Чем больше значение коэффициента, тем больше прибыли на риск одной и той же суммы.
Формула расчета выглядит следующим образом:
Доходность актива
Доходность можно измерять с любой периодичностью – это может быть день, неделя, месяц, или год. Также, в качестве показателя доходности можно брать средний прирост на сделку. Единственное, желательно, чтобы исходные данные доходности должны быть нормально распределены. Отсюда и главная слабость коэффициента. Резкие пики на выборке в 3 и более стандартных отклонения и ассиметричное распределение (видимый наклон графика) могут стать причиной ложной оценки.
Безрисковый доход
Безрисковкый доход – это теоретический доход с нулевым риском. То есть, это та доходность, которую инвестор может получить абсолютно без риска за какой-то определенный период времени. По идее, – это минимальный доход, который инвестор ожидает получить от любой инвестиции. Сравнивая этот показатель с реальным доходом, можно определить, насколько хорошую компенсацию вы получаете за дополнительный риск.
На практике, понятия инвестиции с нулевым риском не существует, так как даже самые безопасные инвестиции несут с собой некоторую долю риска. Тем не менее, к безрисковой доходности можно отнести депозит в сбербанке, либо деньги, инвестированные в казначейские облигации США. Рынок форекс – это всегда инвестиции с высоким риском, поэтому безрисковая доходность в нашем случае будет равна нулю. Но, если ваш депозит хранится в банке, в формулу можно подставить значение текущей базовой ставки.
В терминале MT4 показатель Шарпа считается, как отношение среднеарифметической доходности сделки к стандартному отклонению, при нулевом значении безрисковой ставки.
Полная формула выглядит так:
Стандартное отклонение
Коэффициент Шарпа оценивает эффективность инвестиции с точки зрения дисперсии доходов. Так как мы уже подсчитали избыточную доходность (доходность за вычетом безрисковой ставки), осталось поделить это значение на стандартное отклонение доходности актива. То есть, посчитать отношение доходности к риску.
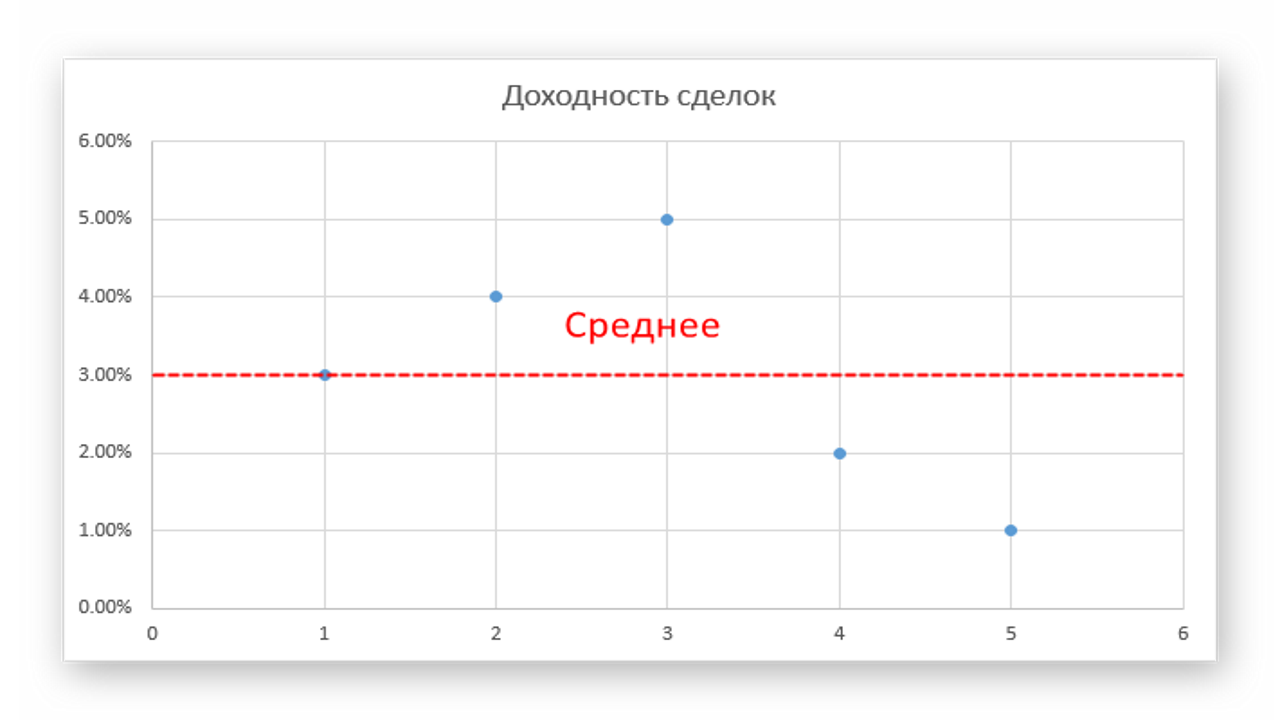
Далее, возводим значения в квадрат, получаем арифметическое среднее и выводим корень от результата – sqrt((0.00% + 0.01% + 0.04% + 0.01% + 0.04%) / 5) = 1.41%.
Для сравнения, возьмем немного другую выбрку: 2%, 8%, 5%, 4%, 6%. Очевидно, что доходность такой системы в рамках рассматриваемого периода больше, но мы также наблюдаем гораздо большую волатильность доходности, 2% против 1.41% у предыдущего примера. Соответственно, первая стратегия является менее рискованной.
Единицы расчёта коэффициента Шарпа
Для примера, попробуем сравнить эффективность двух торговых стратегий по показателям их доходности и риска. Допустим, первая стратегия дает 5% прибыли на сделку, при стандартном стандартном отклонении (показатель дисперсии доходности) равном 4%. Вторая стратегия в среднем приносит по 2% в каждой сделке, но отклонение не превышает 1%. В данном случае, первая стратегия будет иметь коэффициент шарпа 1.25, а вторая – 2.0. Это означает, что не смотря на меньшую доходность, вторая стратегия имеет лучшее соотношение риска к доходности.
Коэффициент Шарпа должен быть равен одному или выше. Тогда считается, что стратегия, которую мы анализируем, работает с достаточной эффективностью. Значение больше трех уже говорит о том, что вероятность получения убытка в каждой сделке меньше 1%. И чем больше полученное значение, тем лучше.
Вывод
В большинстве случаев, коэффициент Шарпа покажет реальную рентабельность стратегии. Но, иногда, показатель Шарпа может вводить в заблуждение. Например, некоторые облигации могут показывать стабильную доходность выше банковского процента в течении многих лет, на что коэффициент ответит нереалистично высокими показателями. В этом случае, полученное значение ничего не скажет о реальных рисках, стоящих за инвестированием в данную облигацию, пусть даже риск будет на самом деле минимальным. В целом же, данный коэффициент подойдёт для сравнения двух стратегий с относительно частыми входами и не самыми огромными целями.
Что такое Коэффициент Шарпа? Расчет, Недостатки и отличие от Сортино
За прошедшие годы статистики, экономисты и математики разработали несколько методов для измерения эффективности торгуемых активов, таких как акции, товары и валюты.
Одной из таких мер является коэффициент Шарпа, который был введен в 1966 году Уильямом Шарпом: почетным профессором финансов в Стэнфорде.
С тех пор это соотношение оказалось ценным инструментом, используемым инвесторами для оценки отдачи от инвестиций по сравнению с их риском.
Коэффициент Шарпа популярен среди трейдеров и управляющих фондами / портфелями благодаря своей простоте. Другой причиной его популярности является тот факт, что профессор Шарп получил Нобелевскую премию 1990 года по экономическим наукам. По этой причине инвесторы регулярно используют его при покупке акций.
Что такое Коэффициент Шарпа?
Это соотношение позволяет инвесторам определить, какую часть прибыли они получат в зависимости от волатильности, которую они будут испытывать при удержании актива.
Это означает, что актив или портфель с более высоким коэффициентом Шарпа рассматривается как лучший выбор по сравнению с другими инвестициями в той же категории.
Такое более высокое соотношение просто приводит к высокой доходности при минимальном риске инвестиций.
Расчет коэффициента Шарпа
При расчете коэффициента Шарпа используется следующая формула:
Это может быть определено с использованием различных периодов времени: ежедневно, еженедельно, ежемесячно или ежегодно.
Выполняя такие расчеты, инвесторы считают T-Bill самым безопасным активом на финансовых рынках, поскольку он поддерживается министерством финансов.
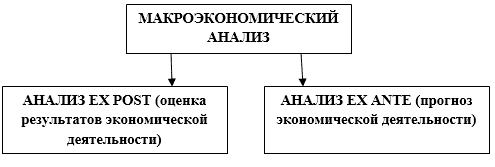
Сравнение Ex-Ante и Ex-Post Шарпа
Одним из преимуществ коэффициента Шарпа является маневренность при выборе типа данных о производительности для ввода в расчеты.
С одной стороны, коэффициент Шарпа можно использовать для оценки прошлых результатов инвестиций или портфеля. В этом случае фактические доходы используются в формуле.
Такое соотношение Шарпа называется «Ex-Post». Термин «Ex-Post» означает «после факта». Такое соотношение Шарпа может быть дополнительно использовано для прогнозирования будущих доходов от инвестиционного выбора с достаточными прошлыми данными.
В случае инвестиций или портфеля без адекватных прошлых данных о производительности инвестор может использовать ожидаемую производительность для расчета так называемого коэффициента Ex-Ante Шарпа.
Термин «Ex-Ante» означает «до факта», и такое соотношение Шарпа основано на оценках и / или прогнозируемых показателях.
Что говорит нам коэффициент Шарпа?
Через общую формулу и ее отдельные составляющие мы также понимаем, что коэффициент Шарпа дает нам количественную оценку эффективности инвестиционного выбора по отношению к риску, принимаемому при владении активом.
Как только коэффициент Шарпа будет определен, потенциальные инвестиции могут быть классифицированы следующим образом:
Значение меньше 1 означает плохие инвестиции
Например, предположим, что мы анализируем два разных портфеля, которые составляют разные акции. После необходимых расчетов первый портфель определен для обеспечения доходности 14%.
Однако с такими высокими доходами обычно наблюдается высокая волатильность. В этом случае волатильность была определена как 9%.
Второй портфель также был оценен и потенциально может обеспечить доходность 8,5% с меньшей волатильностью 4%. Используя гипотетический Treasury Bill с безрисковой доходностью 3%, мы получаем следующие сравнения между двумя портфелями.
| 1-е портфолио | 2-е портфолио | |
|---|---|---|
| Норма прибыли | 14 | 8.5 |
| Безрисковая норма прибыли | 3 | 3 |
| Волатильность | 9 | 4 |
| Коэффициент Шарпа | (14-3) / 9 = 1,22 | (8,5-3) / 4 = 1,375 |
Все инвестиции направлены на максимизацию прибыли и в то же время на снижение риска. В этом случае желательно второе портфолио.
Кроме того, используя эти два примера, мы дополнительно понимаем экспоненциальную связь между волатильностью актива и коэффициентом Шарпа.
Чем ниже волатильность, тем выше коэффициент Шарпа. И наоборот, чем выше волатильность, тем ниже коэффициент Шарпа.
Недостатки коэффициента Шарпа
Одним из недостатков коэффициента Шарпа является использование стандартного отклонения доходности для измерения доходности инвестиций.
Стандартное отклонение основано на предположении, что доходы распределяются равномерно. Однако трейдеры и инвесторы знают, что ценовые движения на финансовых рынках не всегда распределяются равномерно в течение определенного периода времени.
В некоторые торговые дни наблюдается значительный всплеск из-за какого-то случайного события. В другие дни рынок находится в минусе из-за того, что трейдеры извлекают выгоду из явной возможности открывать короткие позиции на основе технических индикаторов.
Вторым недостатком коэффициента Шарпа является простая способность некоторых портфельных менеджеров манипулировать своими ресурсами для укрепления своей репутации. Это можно сделать, используя более длительный период времени для измерения волатильности, что приводит к снижению значения.
Портфельный менеджер может принять решение использовать стандартное отклонение в течение нескольких месяцев, а не нескольких дней. Первый набор данных обеспечивает более низкую оценку волатильности по сравнению со вторым.
В-третьих, управляющий портфелем может принять решение о выборке данных за период времени, когда волатильность была однородной или отсутствовала. Таким образом, преднамеренно выбирая набор данных, менеджер портфеля может искажать окончательное значение коэффициента Шарпа для своей выгоды.
Отличие Шарпа от Сортино
Именно из-за некоторых из этих ограничений коэффициента Шарпа некоторые управляющие фондами и трейдеры предпочитают использовать коэффициент Сортино.
В отличие от коэффициента Шарпа, коэффициент Сортино не учитывает общую волатильность инвестиций. Он измеряет эффективность инвестиций по отношению к риску снижения инвестиций.
Вывод
Подводя итоги, розничные и институциональные инвесторы нуждаются в надлежащем методе количественной оценки прибыли по отношению к риску при выборе инвестиционного выбора.
Прогнозирование потенциальной доходности недостаточно при оценке жизнеспособности инвестиций в течение определенного периода времени.
Коэффициент Шарпа обеспечивает лучшее представление о привлекательности инвестиций благодаря включению риска в их расчет. Это позволяет инвесторам лучше понять доходность по отношению к риску, принимаемому при владении активом.
Однако, как и во всех отношениях, коэффициент Шарпа имеет свои недостатки. Он использует стандартное отклонение при условии, что доходы распределяются равномерно. В связи с этим некоторые трейдеры и инвесторы предпочитают использовать коэффициент Сортино, который при расчете использует только стандартное отклонение в сторону понижения.