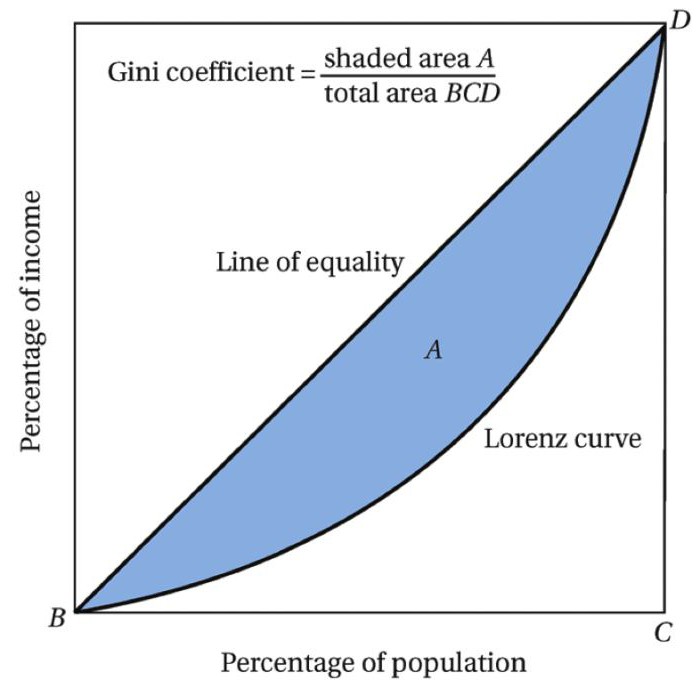
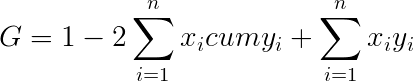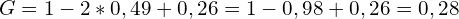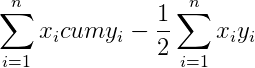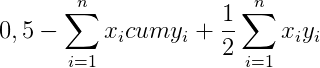Свойства кривой лоренца таковы что
Кривая Лоренца
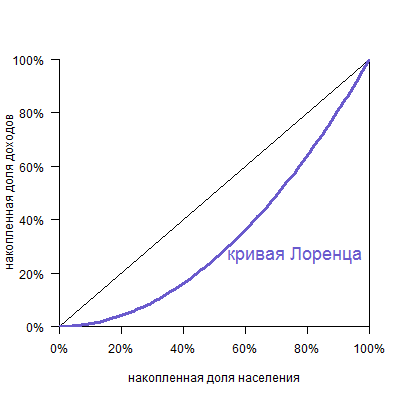
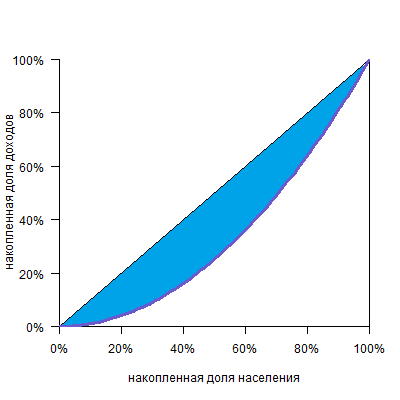
Кривая Лоренца (Lorenz curve) — график, демонстрирующий степень неравенства в распределении дохода в обществе, отрасли, а также степени неравенства в распределении богатства. Если обратиться к кривой Лоренца показывающей степень неравенства в распределении дохода в обществе, то график или кривая Лоренца будет отражать долю дохода, приходящуюся на различные группы населения сформированные на основании размера дохода, который они получают.
Неравенство доходов в конце XIX — начале XX века стало объектом изучения многих экономистов США и Западной Европы. Центральной проблемой изучения является оценка справедливости и эффективности сложившегося в рыночной экономике распределения доходов и богатства. В 1905 году американский статистик Макс Лоренц разработал метод оценки распределения доходов, получивший название кривой Лоренца.
На оси абсцисс откладывается доля населения, а на оси ординат — доля доходов в обществе в процентном отношении. Как видно из графика, в обществе всегда имеет место быть неравенство в распределении доходов, что отражает кривая \mathrm
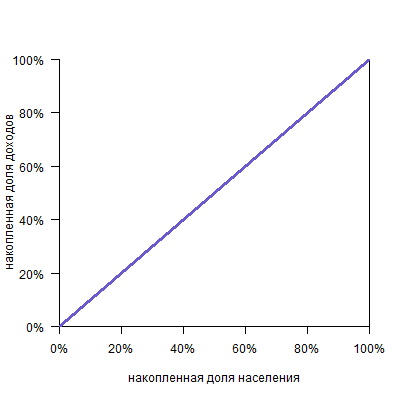
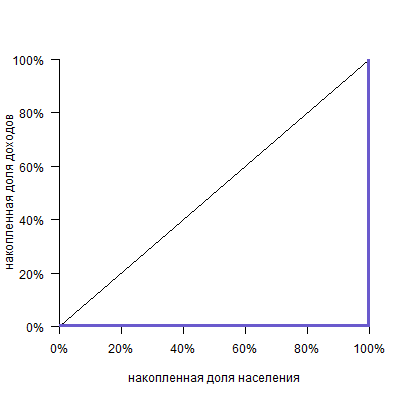
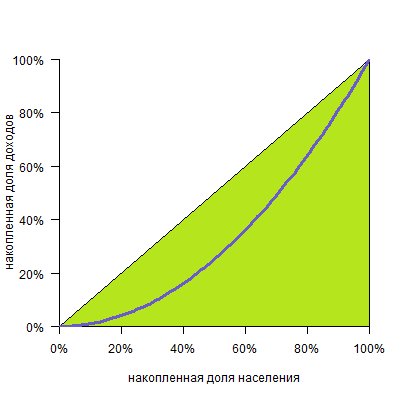
Если бы в обществе было бы равное распредение дохода, то кривая Лоренца приняла бы вид прямой (биссектриса на графике), называемая линией абсолютного равенства, и, наконец, если бы в обществе весь доход получали только 1% населения, то на графике это выразилось бы вертикальной прямой линией, называемой линией абсолютного неравенства.
На основании кривой Лоренца можно вывести коэффициент Джинни.
Кривая Лоренца
Что такое Кривая Лоренца?
Кривая Лоренца – это графическое изображение неравенства доходов или неравенства богатства, разработанное американским экономистом Максом Лоренцем в 1905 году. График отображает процентили населения на горизонтальной оси в зависимости от дохода или богатства. Он отображает совокупный доход или богатство на вертикальной оси, так что значение x, равное 45, и значение y, равное 14,2, означало бы, что нижние 45% населения контролируют 14,2% общего дохода или богатства. На практике кривая Лоренца обычно представляет собой математическую функцию, оцениваемую на основе неполного набора наблюдений за доходом или богатством.
Ключевые моменты
Понимание кривой Лоренца
Кривая Лоренца обычно начинается с эмпирического измерения богатства или распределения доходов среди населения на основе таких данных, как налоговые декларации, в которых указывается доход большой части населения. График данных можно использовать непосредственно как кривую Лоренца, или экономисты и статистики могут подобрать кривую, которая представляет собой непрерывную функцию, чтобы заполнить любые пробелы в наблюдаемых данных.
Кривая Лоренца дает более подробную информацию о точном распределении богатства или дохода среди населения, чем сводные статистические данные, такие как коэффициент Джини или коэффициент асимметрии Лоренца. Поскольку кривая Лоренца визуально отображает распределение по каждому процентилю (или другой единице разбивки), она может точно показать, в каком процентиле дохода (или богатства) наблюдаемое распределение отличается от линии равенства и насколько.
Однако, поскольку построение кривой Лоренца включает подгонку непрерывной функции к некоторому неполному набору данных, нет гарантии, что значения вдоль кривой Лоренца (кроме тех, которые фактически наблюдаются в данных) действительно соответствуют истинному распределению доходов. Большинство точек на кривой – это просто предположения, основанные на форме кривой, которая лучше всего соответствует наблюдаемым точкам данных. Таким образом, форма кривой Лоренца может быть чувствительной к качеству и размеру выборки данных, а также к математическим допущениям и суждениям относительно того, что представляет собой кривую наилучшего соответствия, и они могут представлять источники существенной ошибки между кривой Лоренца и фактическим распространение.
Пример кривой Лоренца
Коэффициент Джини используется для выражения степени неравенства одной цифрой. Он может варьироваться от 0 (или 0%) до 1 (или 100%). Полное равенство, при котором каждый человек имеет одинаковый доход или богатство, соответствует коэффициенту 0. Если нарисовать кривую Лоренца, полное равенство будет прямой диагональной линией с наклоном 1 (площадь между этой кривой и самой кривой равна 0, поэтому коэффициент Джини равен 0). Коэффициент 1 означает, что один человек получает весь доход или владеет всем богатством. С учетом отрицательного богатства или дохода цифра теоретически может быть больше 1; в этом случае кривая Лоренца опустится ниже горизонтальной оси.
Кривая выше показывает непрерывную кривую Лоренца, которая была подогнана к данным, описывающим распределение доходов в Бразилии в 2015 году, по сравнению с прямой диагональной линией, представляющей полное равенство. На 55-м процентиле дохода значение кривой Лоренца составляет 20,59%: другими словами, эта кривая Лоренца оценивает, что нижние 55% населения получают 20,59% общего дохода страны. Если бы Бразилия была абсолютно равноправным обществом, нижние 55% зарабатывали бы 55% от общей суммы. 99-й процентиль соответствует 88,79% совокупного дохода, что означает, что на верхний 1% приходится 11,21% дохода Бразилии.
Чтобы найти приблизительный коэффициент Джини, вычтите площадь под кривой Лоренца (около 0,25) из площади под линией полного равенства (0,5 по определению). Разделите результат на площадь под линией полного равенства, что даст коэффициент около 0,5 или 50%. По данным ЦРУ, коэффициент Джини Бразилии в 2014 году составлял 49,7%.
Как рассчитывать коэффициент Джини
Автор: Игорь Святославович Демин · Опубликовано 21.11.2017 · Обновлено 19.01.2021
Что такое кривая Лоренца, коэффициент Джини (индекс Джини) и как их рисовать и считать?
Начнем с кривой Лоренца.
Кривая Лоренца
Кривая Лоренца — это график, демонстрирующий степень неравенства в распределении дохода или богатства в обществе. Ее придумал в 1905 году американский статистик Макс Лоренц.
Собственно говоря, эта кривая может отражать неравенство в распределении самых разных величин, но вначале она предназначалась именно для отражения экономического неравенства в обществе.
Кривая выглядит следующим образом:
По горизонтальной оси указана накопленная доля населения (причем население отсортировано от беднейших, то есть получающих наименьший доход, до богатейших), а по вертикальной — доля получаемого дохода.
Это лучше понять на примере:
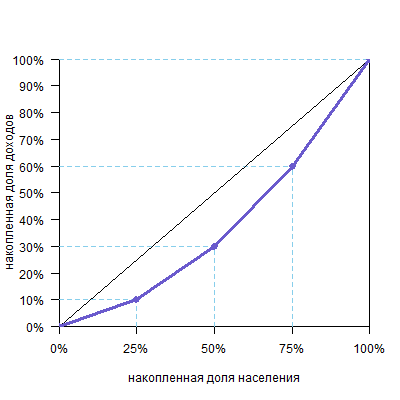
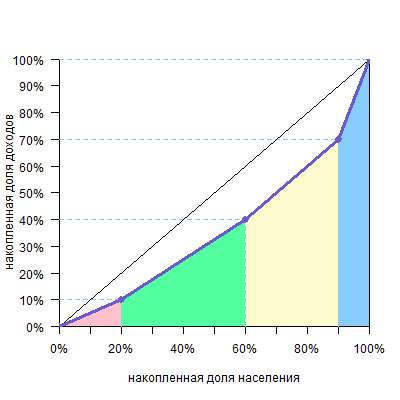
Предположим, мы разбили все население страны на 4 группы, в каждой из которых по 25% населения. При этом первая, «бедная» группа получает 10% общего дохода страны, вторая, «ниже среднего» — 20%, третья, «выше среднего» — 30% и четвертая, «богатая» — 40%.
| Группа | Доля населения | Доля от общего дохода |
| бедная | 25% | 10% |
| ниже среднего | 25% | 20% |
| выше среднего | 25% | 30% |
| богатая | 25% | 40% |
Теперь переведем это в накопленные доли: 25% населения будут получать 10%, 50% населения (это «бедная» и «ниже среднего» группы) суммарно получают 10%+20%=30%, 75% населения («бедная», «ниже среднего» и «выше среднего» группы) получат 10%+20%+30%=60% всего дохода, и, разумеется, 100% населения получат 100% дохода.
| Накопленная доля населения | Накопленная доля общего дохода |
| 25% | 10% |
| 50% | 30% |
| 75% | 60% |
| 100% | 100% |
Теперь можно построить график.
Обратите внимание, что кривая всегда исходит из точки (0%;0%) и приходит в точку (100%;100%), так как ясно, что 0% населения получают 0% дохода, а 100% населения получают 100% дохода.
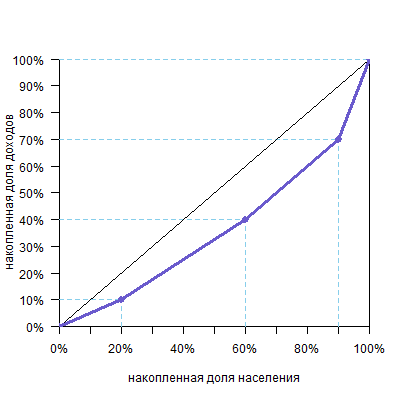
Необязательно, чтобы группы были равными. Например, возьмем такие данные:
| Доля населения | Доля от общего дохода | Накопленная доля населения | Накопленная доля общего дохода |
| 20% | 10% | 20% | 10% |
| 40% | 30% | 60% | 40% |
| 30% | 30% | 90% | 70% |
| 10% | 30% | 100% | 100% |
Обратите внимание, что группы нужно распределить от бедных к богатым. Если группы одинаковые, то они сортируются просто по столбцу «Доля от общего дохода» — от маленьких значений к большим (см. прошлый пример). Но у нас группы разного размера, поэтому нужно учитывать отношение второго столбца к первому (доли дохода к доле населения). Например, у нас вторая и третья группы получают одинаковую долю дохода. Но во второй группе населения больше, а значит, в расчете на одного человека они беднее. То же с третьей и четвертой группой. Вообще говоря, случай с разными группами редкий и встречается только в условных задачах. Но если будут такие условия, то нужно делить долю дохода на долю населения. Для наших групп получим:
Это значит, что в третьей группе население получает именно средний по стране доход на человека. В первой группе доход в два раза ниже среднего, во второй — 75% от среднего, а в четвертой — три средних дохода на человека. Вот в таком порядке их и нужно расположить для построения кривой Лоренца.
Получим такой график:
И, конечно, количество групп может быть любым. Желательно, чтобы их было побольше, тогда кривая будет построена по большему числу точек, станет более гладкой и точной.
Можно представить себе кривую абсолютно равного распределения: это будет просто диагональ, так как любые N% населения получают N% дохода:
И кривую абсолютного неравенства, когда все работают бесплатно, а один-единственный человек получает весь доход:
(Не думайте, что это совершенно умозрительная кривая: например, если у единственного человека в стране есть, скажем, говорящий еж, то кривая распределения говорящих ежей будет именно такой!)
Коэффициент Джини
К 1912 году итальянский статистик Коррадо Джини разработал алгебраическую интерпретацию кривой Лоренца: коэффициент, призванный указывать, насколько неравным является экономическое распределение.
Все очень просто. Коэффициент этот равен отношению площади фигуры между диагональю и кривой Лоренца:
К площади треугольника под диагональю (а она всегда равна 0,5):
Таким образом, при полном равенстве площадь первой фигуры равна нулю, и коэффициент тоже равен нулю. При полном неравенстве эта фигура займет весь треугольник и коэффициент будет равен единице.
Чем ниже коэффициент, тем более равным является распределение.
Как его считать?
Считать коэффициент Джини можно графическим или алгебраическим способом. Посмотрим, как это можно сделать.
Графический способ
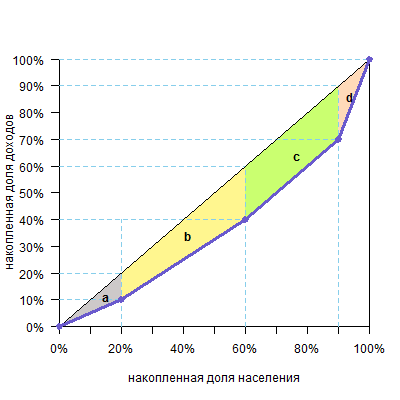
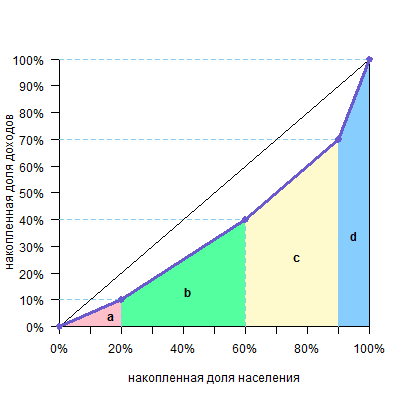
Вертикальными линиями можно разделить фигуру над кривой Лоренца на два треугольника и несколько трапеций.
Площадь треугольника — половина основания на высоту, а трапеции — полусумма оснований на высоту (поверните голову на 90º, высоты расположены горизонтально, а основания — вертикально). Высоты равны размерам групп, а основания легко посчитать. В нашем случае площадь фигуры будет такой:
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+20%)/2*40%=0,3/2*0,4 | 0,06 |
| трапеция c | (20%+20%)/2*30%=0,4/2*0,3 | 0,06 |
| треугольник d | 20%*10%/2=0,2*0,1/2 | 0,01 |
| Всего площадь фигуры (a+b+c+d) | 0,14 |
Теперь разделим ее на площадь треугольника под диагональю (а он, напоминаю, всегда равен 0,5) и получим: 0,14/0,5=0,28
Таким образом, 0,28 или 28% и есть значение коэффициента Джини.
Другой графический способ: посчитать площадь фигур под кривой Лоренца, а затем вычесть их из площади треугольника под диагональю (0,5) и получить площадь над кривой. И ее уже разделить на 0,5.
Этот случай удобнее, когда цифры не такие круглые и ширина оснований трапеций над кривой неочевидна.
| фигура | расчет площади | площадь |
| треугольник a | 10%*20%/2=0,1*0,2/2 | 0,01 |
| трапеция b | (10%+40%)/2*40%=0,5/2*0,4 | 0,1 |
| трапеция c | (40%+70%)/2*30%=1,1/2*0,3 | 0,165 |
| трапеция d | (70%+100)%/2*10%=1,7/2*0,1 | 0,085 |
| Всего площадь фигуры (a+b+c+d) | 0,36 |
Отнимаем 0,36 от 0,5 и получаем 0,14 — площадь фигуры над кривой
Далее, как и в первом способе, делим эту площадь на 0,5 (площадь треугольника под диагональю) и получаем: 0,14/0,5=0,28
Алгебраический способ
Наиболее проста в употреблении формула:
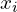
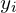
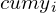
Составим таблицу на основе данных предыдущего примера:
| Доля населения ( 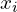 ) ) | Доля от общего дохода ( 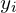 ) ) | Накопленная доля общего дохода ( 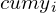 ) ) | 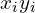 | 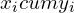 |
| 20% | 10% | 10% | 0,02 | 0,02 |
| 40% | 30% | 40% | 0,12 | 0,16 |
| 30% | 30% | 70% | 0,09 | 0,21 |
| 10% | 30% | 100% | 0,03 | 0,1 |
| Итого | 0,26 | 0,49 |
Если вы не понимаете, как построена эта таблица, откройте спойлер:
Как построена эта таблица
Первый и второй столбцы — это исходные данные, они такие же, как и в разделе «Графический способ».
Третий столбец получается из второго путем накопления значений из второго столбца: берем значение из ячейки слева и всех ячеек выше нее и складываем.
Четвертый столбец — произведение первого и второго.Чтобы не запутаться в процентах, переведите их в доли, например для первой строки: 20%10%=0,20,1=0,02.
Пятый столбец — произведение первого и третьего.
Далее подсчитываем суммы по четвертому и пятому столбцу.
Теперь можно подставить полученные суммы в формулу, которая приведена выше:
Мы получили ответ 0,28 — такой же, как и графическим методом.
Это самая простая в применении формула. Советую ее запомнить. А если вдруг хочется понять, как она выведена, откройте этот спойлер (объяснение довольно длинное!):
Как выведена эта формула?
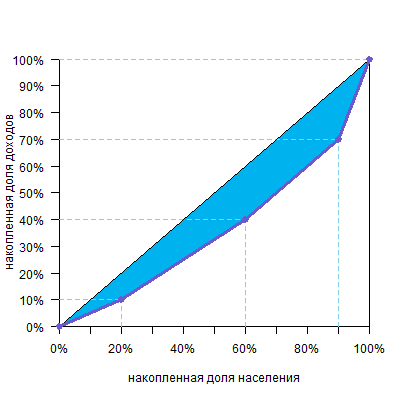
В основе этой формулы лежит уже известная вам идея: чтобы посчитать площадь фигуры над кривой Лоренца:
можно сперва посчитать площадь фигуры под кривой Лоренца
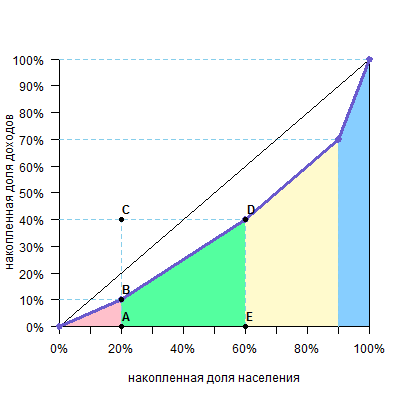
а потом вычесть ее из площади диагонального треугольника, которая равна 0,5, и получим искомое. Саму же площадь под кривой будем считать по группам. Можно видеть, что над каждой группой образуется треугольник или четырехугольник — они выделены разными цветами.
Рассмотрим, например, вторую группу (зеленый четырехугольник).
Площадь четырехугольника ABDE равна площади прямоугольника ACDE минус площадь прямоугольного треугольника BCD. При этом площадь прямоугольника ACDE равна AEDE, а площадь прямоугольного треугольника BCD равна CDBC/2. Таким образом, площадь ABDE равна
При этом можно увидеть на графике, что ВС — доля дохода по группе (y), DE — накопленная доля дохода по группе (cum y), а AE или CD — доля группы в численности населения (x). Тогда формула принимает вид
Можно видеть, что такая формула (прямоугольник минус прямоугольный треугольник) пригодна для всех цветных фигур, включая и левый розовый треугольник.
Тогда сумма всех фигур под кривой Лоренца будет равна
Эту сумму, как вы помните, нужно вычесть из 0,5, чтобы получить площадь фигуры над кривой
И наконец, разделив все это на площадь диагонального треугольника (то есть опять же на 0,5), получим формулу коэффициента Джини:
Есть и другие формулы, расчет по одной из них приведен, например, вот тут. Мне кажется, что в ней проще запутаться, а получается ровно то же самое.
Чтобы проверить себя, решите задачу. Ответ и решение под спойлерами:
Задача
Предположим, что в некоторой стране N проживают три группы населения: бедные, средний класс и богатые. Группы равны по численности жителей, но различаются по уровню дохода: средний класс зарабатывает в два раза больше, чем бедные, а богатые зарабатывают в два раза больше, чем средний класс. Внутри групп доходы распределены равномерно. Нарисуйте график кривой Лоренца и рассчитайте коэффициент Джини.\
Кривая Лоренца
СОДЕРЖАНИЕ
Объяснение [ править ]
Данные за 2005 год.
Точки на кривой Лоренца представляют такие утверждения, как «нижние 20% всех домохозяйств имеют 10% общего дохода».
Совершенно равное распределение доходов будет таким, при котором все люди имеют одинаковый доход. В этом случае у нижних N % общества всегда будет N % дохода. Это можно изобразить прямой y = x ; называется «линией идеального равенства».
F я знак равно Σ j знак равно 1 я ж ( y j ) <\ Displaystyle F_ : = \ Sigma _ 

Когда все y i равновероятны с вероятностями 1 / n, это упрощается до
В качестве альтернативы, для кумулятивной функции распределения F ( x ) с обратным x ( F ) кривая Лоренца L ( F ) непосредственно задается следующим образом:
Обратный x ( F ) может не существовать, потому что интегральная функция распределения имеет интервалы постоянных значений. Однако предыдущая формула все еще может применяться, обобщая определение x ( F ):
Свойства [ править ]
Кривая Лоренца всегда начинается в точке (0,0) и заканчивается в точке (1,1).
Кривая Лоренца не определяется, если среднее значение распределения вероятностей равно нулю или бесконечно.
Кривая Лоренца не может подняться выше линии полного равенства.
Если измеряемая переменная не может принимать отрицательные значения, кривая Лоренца:
Однако обратите внимание, что кривая Лоренца для чистой стоимости сначала будет отрицательной из-за того, что у некоторых людей есть отрицательная стоимость из-за долга.
Кривая Лоренца. Неравенство распределения доходов
Неравенство распределения доходов заложено в самой сущности рыночной экономики. Даже в идеально справедливом обществе оно будет существовать, поскольку все мы отличаемся природными способностями. Неравенство распределения доходов обычно иллюстрирует ситуация, когда маленькая часть населения обладает существенной долей национального богатства, и наоборот. Для его измерения используется, в частности, кривая Лоренца.
Распределение богатства
В любой стране есть богатые и бедные граждане. Первые обладают львиной долей национального богатства, вторые – едва сводят концы с концами. В краткосрочном периоде мы наблюдаем неравенство распределения доходов. В перспективе – несправедливость накопления богатства элитами.
История формирования концепции
Кривая Лоренца
Предположим, мы хотим изобразить несправедливость распределения богатства в государстве. Для этого нам понадобятся доходы населения. Кривая Лоренца строится в четыре этапа:
Кривая Лоренца позволяет визуализировать неравенство распределения доходов. Можно совместить несколько графиков для того, чтобы показать изменения на протяжении времени или сравнить ситуацию в ряде стран.
Как построить кривую Лоренца на практике
Предположим, что в рассматриваемой нами отрасли есть десять фирм, которые различаются по своему вкладу в экономику. Если бы у нас были доходы населения, кривая Лоренца бы показывала неравенство их распределения. В этом случае она иллюстрирует справедливость разделения рынка. Для того чтобы построить кривую Лоренца, в этом случае необходимо:
Коэффициент Джини
Мы рассмотрели особенности построения графика распределения доходов. За визуальную сторону вопроса отвечает кривая Лоренца. Коэффициент Джини оперирует числовыми значениями. Он измеряется соотношением точек на реальном графике с идеальным случаем (прямой линией, которая образует с осью абсцисс угол в 45 градусов). Коэффициент Джини может принимать значения от 0 до 1. В первом случае мы имеем дело с абсолютной справедливостью распределения доходов, во втором – с полным неравенством, когда один человек обладает всем национальным богатством, а другим не остается ничего. Естественно, оба случая нереальны. Однако важно понимать, что меньшее значение коэффициента указывает на лучшую ситуацию в экономике государства.
Проблемы использования коэффициента
Индекс Джини полностью базируется на показателях валового национального продукта и статистике доходов населения. Многие развивающиеся страны не предоставляют точных сведений, что не дает правильно оценить ситуацию с распределением богатства в них. Также существует обратно пропорциональная зависимость между коэффициентом Джини и валовым внутренним продуктом на душу населения. Это связано с тем, что в более бедных странах проблемы существеннее.
Интерпретация показателей
Когда мы разобрались, как построить кривую Лоренца, важно понять, что же все-таки она значит. Как можно сопоставлять страны с различными уровнями ВВП? Кривая Лоренца и коэффициент Джини используются для того, чтобы понять, насколько справедливо распределяется национальное богатство государства. Нужно понимать, что государства с самыми низкими показателями – это необязательно самые богатые страны. Сходные валовые продукты не указывают на одинаковую форму кривой на графике распределения доходов.
Глубина бедности
Неравенство распределения доходов приводит к тому, что 10% населения отрываются на полную, а нижний дециль вынужден выживать на 1,25 доллара США в день. Все, кто зарабатывают меньше этой суммы, вообще считаются живущими за гранью бедности. Однако нужно понимать, что в каждой стране своя цена жизни, поэтому этот стандарт необходимо корректировать с поправкой на национальные особенности.
Группа по исследованию развития Всемирного банка рассчитывает специальный показатель глубины бедности. Для этого используются показатели доходов и потребления домохозяйств 115 стран. Отчеты по показателю выходят два раза в год: в апреле и сентябре.
Социальная политика государства
Высокая степень неравномерности распределения доходов является причиной забастовок и даже революций. Поэтому цель любого правительства состоит в том, чтобы сделать это явление менее заметным и смягчить разрыв между богатыми и бедными. Социальная политика государства обычно связана с развитием справедливых отношений в обществе, формированием защитных механизмов и созданием условий для роста благосостояния населения. Для этого правительству приходится решать следующие задачи:
Выводы
Идеального общества абсолютной справедливости не существует. Есть только государства с большим или меньшим коэффициентом Джини. Чем меньше разрыв между идеальной и реальной кривой Лоренца, тем лучше распределяются доходы в стране. Проблема несправедливости накопления богатства отдельными лицами или группами характерна для многих современных государств, особенно развивающихся. Для частичного решения этой проблемы необходима грамотная национальная социальная политика. Ее результативность оценивают, сравнивая уровень и качество жизни в различных странах или за определенный период. Важно не допустить достижения так называемого социального дна и прогрессирования диспропорциональности. Если государство справляется со своими функциями, то население, даже бедное, должно чувствовать улучшение уровня жизни. И это связано не столько с изменением формы кривой Лоренца, сколько с расширением потребительской корзины. В противном случае в обществе начинает назревать переворот со всеми его негативными последствиями.