Что такое оси координат

Прямоугольная система координат

В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.

Координаты могут обозначаться самыми разными наборами цифр или букв.

Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.

Координаты — это набор данных, по которому определяется положение того или иного объекта.

Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.

Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.

Декартова система координат

Французкий математик Рене Декарт (1596–1650) предложил задавать положение точки на плоскости с помощью двух координат.

Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.

Оси взаимно перпендикулярны (т.е. угол между ними равен 90° ) и пересекаются в точке, которую обозначают « O ». Точка « O » является началом отсчёта для каждой из осей.

Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.

Координатные оси — это прямые, образующие систему координат.

Ось абсцисс « Ox » — горизонтальная ось.

Ось ординат « Oy » — вертикальная ось.

Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как « x0y ».

Обращаем ваше внимание на выбор длины единичных отрезков по осям.

Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси « Oy ». Цифры на оси « Ox », как правило, пишут внизу под осью.

Обычно единичный отрезок на оси « 0y » равен единичному отрезку на оси « 0x ». Но бывают случаи, когда они не равны друг другу.

Отсчитываем четверти (или координатные углы) против часовой стрелки.

Источник

Прямоугольная система координат

Содержание

Иногда в жизни, чтобы найти на плоскости какой-то объект, его описывают двумя значениями. Так каждое место в зале кинотеатра имеет два параметра: ряд и место. Каждая клетка на шахматной доске или при игре в «морской бой» описывается номером строки и буквой, обозначающей столбец.

В математике определение местоположения объекта на плоскости придумали быстро находить с помощью системы координат, образованной двумя прямыми, называемых координатными осями (или осями координат).

Ось координат

Абсцисса, ордината, начало координат и единичный отрезок

Оси пересекаются под прямым углом перпендикулярно друг к другу, поэтому такая система координат и называется прямоугольной.

На каждой оси выбирается единичный отрезок, с помощью которого вычисляются координаты объекта. Длиной единичного отрезка может выступать любая единица измерения, но она должна быть одинаковой на каждой из осей. То есть, если единичный отрезок на оси абсцисс задан, например, равным 1 см, то и на оси ординат единичный отрезок тоже должен быть равен одному сантиметру.

Абсцисса, ордината, начало координат и единичный отрезок

Положительное и отрицательное направление

У осей стрелкой задается положительное направление:

Таким образом, все вместе:

образуют в математике прямоугольную систему координат, плоскость называют координатной.

Или другими словами:

Четверти

Осями координат плоскость делится на 4 части, их обозначают римскими цифрами. Каждая часть называется «квадрант». Другие названия: «координатный угол» или «четверть». Нумерация четвертей принята против часовой стрелки в том порядке, в котором указано на рисунке ниже.

Четверти координатной плоскости

Немного из истории

В латинском языке слово «координаты» получилось из двух других: co – «совместно» и ordinatus – «определенный», «упорядоченный».

Впервые необходимость нахождения координат объектов возникла в географии и астрономии. Для этого использовали широту и долготу, определяющие расположение точки на небесной сфере или на поверхности земного шара. Таким образом начали вычислять координаты точек еще в 14 веке. Но упорядочил и систематизировал все знания в 17 веке французский математик по имени Рене Декарт. Поэтому прямоугольную систему координат также называют еще и «декартовой».

Источник

Координаты. Декартова система координат.

Координаты – совокупность данных, на основании которых точно характеризуется местоположение объекта.

Рене Декарт (1596–1650) предложил представлять местоположение точки на плоскости при помощи пары координат.

Для характеристики координат требуются ориентиры. Данными ориентирами на плоскости выступают две числовые оси. Сначала чертят горизонтальную ось, её принято определять как ось абсцисс и подписывать буквой х, указывают, что это ось 0х. Положительное направление на оси абсцисс принято слева на право и указывается стрелкой.

Следующей чертят вертикально ось, её принято определять как ось ординат и подписывать буквой у, указывают, что это ось 0у. Положительное направление на оси ординат принято снизу вверх и указывается стрелкой.

Оси пересекаются под углом 90°, то есть являются взаимно перпендикулярными. Точку их пересечения обозначают как «0». Точку «0» принято считать исходной точкой для отсчёта по каждой из осей.

Система координат — это две взаимно перпендикулярные координатные прямые, которые пересекаются в месте, являющемся началом отсчёта для каждой из них.

Координатные оси — это прямые, формирующие систему координат.

Ось абсцисс (0x) — расположенная горизонтально ось.

Ось ординат (0y) —расположенная вертикально ось.

Координатная плоскость — плоскость, в которой сформирована система координат. Для обозначения данной плоскости применяют x0y.

Цифры, указывающие числовые значения на осях размещают как по правую, так и по левую сторону от оси 0y. Цифры на оси 0x принято указывать внизу под осью.

Чаще всего единичные отрезки по оси 0y и оси 0x одинаковы. Но встречаются ситуации, когда они не равны друг другу.

Оси координат разделяют плоскость на 4 угла, которые обозначают как координатные четверти. Четверть, сформированная положительными полуосями (правый верхний угол), принято считать первой (I). Остальные четверти (координатные углы) располагаем против часовой стрелки.

Источник

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Прямоугольная система координат в трехмерном пространстве

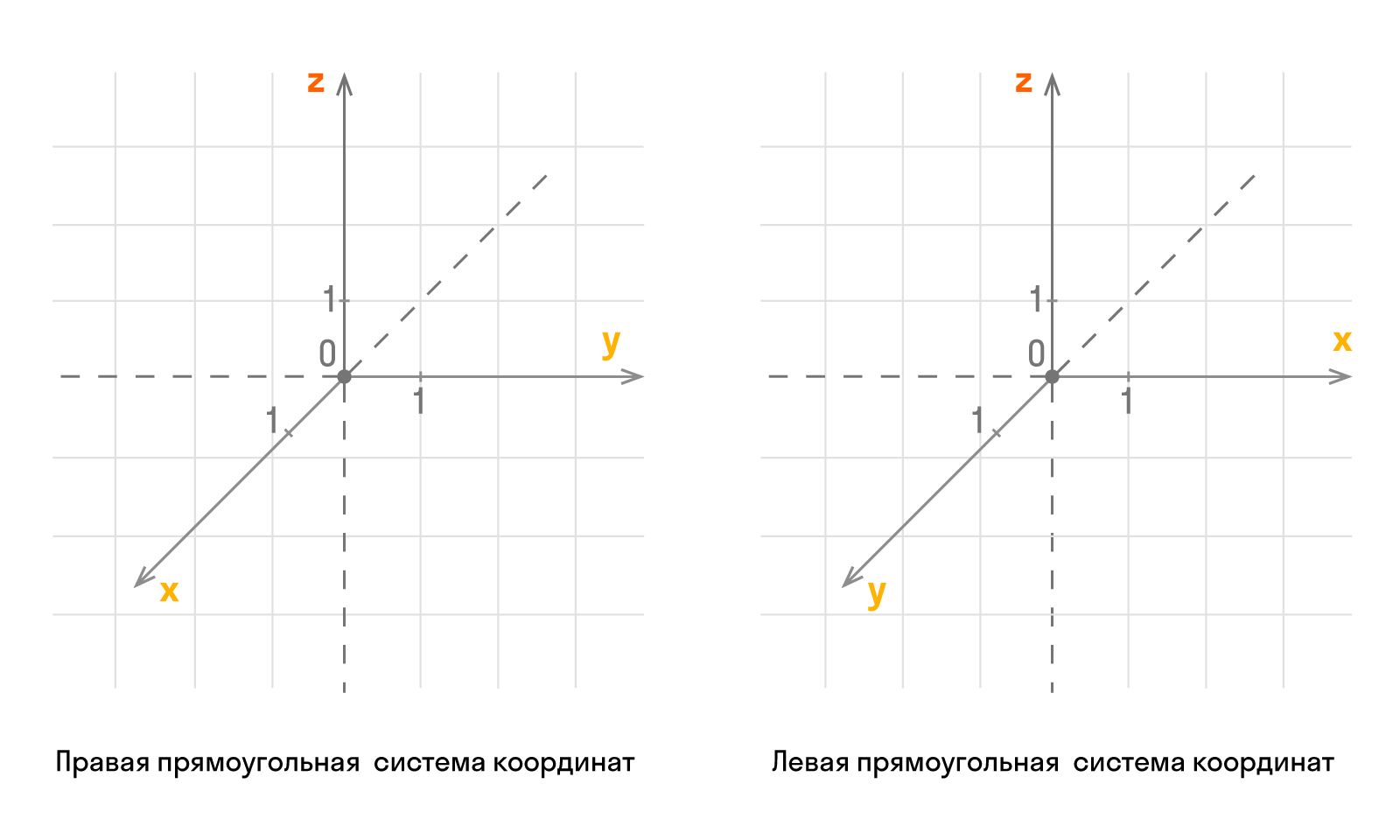
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

Сформулируем определение точки М в трехмерном пространстве.

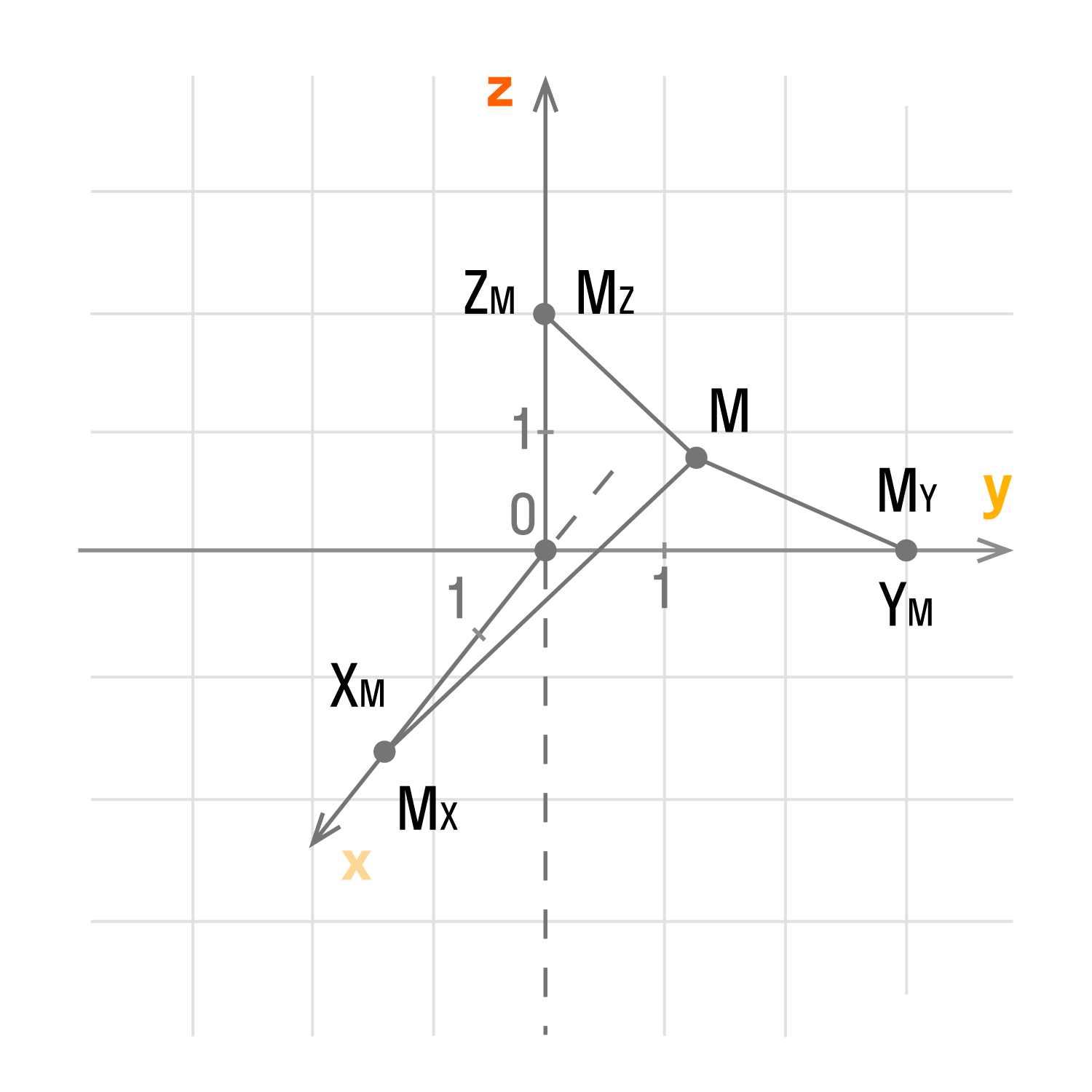
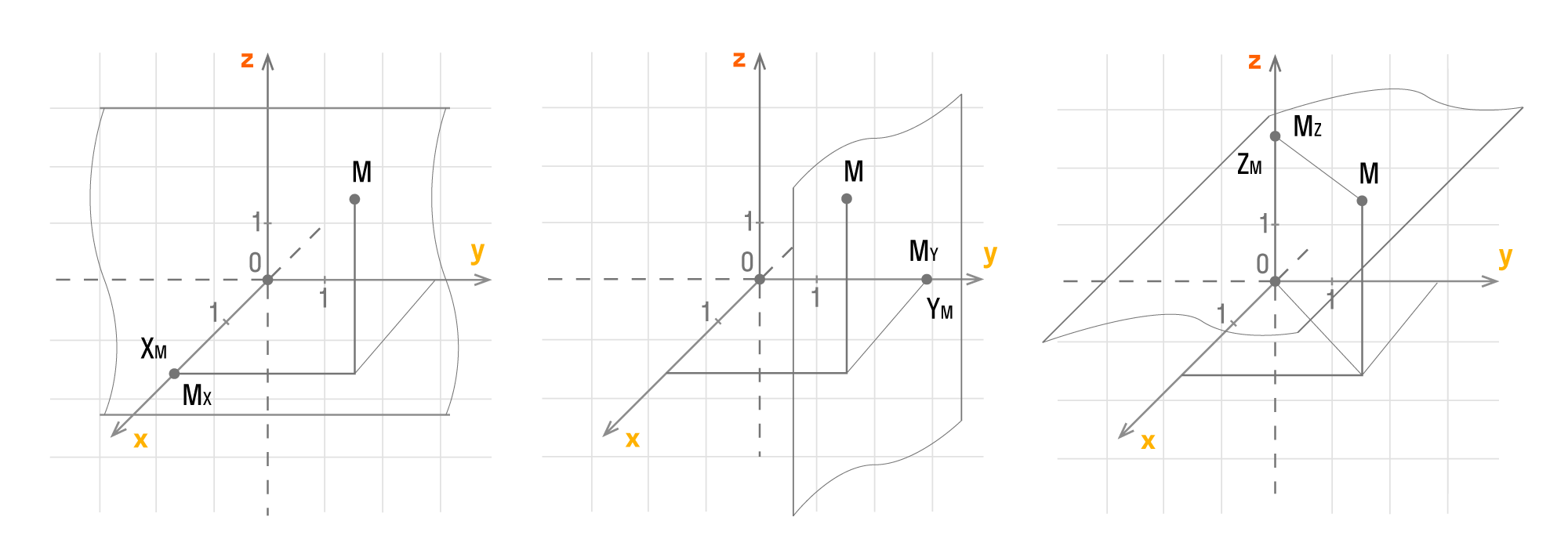
Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Источник

Математика. 6 класс

Конспект урока

Декартова система координат на плоскости

Перечень рассматриваемых вопросов:

Координатная плоскость. Зададим на плоскости две оси координат, расположив их под прямым углом. Координатные оси пересекаются в точке, являющейся началом отсчёта для каждой из них.

Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.

Оси координат разделяют плоскость на 4 угла, которые называются координатными четвертями.

Координаты точки М (х; у), где х – абсцисса, у – ордината точки.

Теоретический материал для самостоятельного изучения

Зададим на плоскости две оси координат, расположив их под прямым углом. Единичные отрезки осей возьмём равными друг другу.

Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.

Положительное направление на осях указывается стрелкой.

Точку пересечения осей называют началом координат.

Оси взаимно перпендикулярны, поэтому заданную таким образом систему координат называют прямоугольной.

Оси координат разделяют плоскость на 4 угла – координатные четверти. Обозначают римскими цифрами как показано на рисунке.

Одним из первых, кто начал широко использовать прямоугольную систему координат в своих исследованиях, был французский философ и математик Рене Декарт, поэтому её часто называют декартовой системой координат.

Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, параллельные осям координат. Прямая, параллельная оси y, пересечёт ось x в точке A₁, а прямая, параллельная оси x, пересечёт ось y в точке A₂. Координату точки A₁ на оси x называют абсциссой точки A. Координату точки A₂ на оси y называют ординатой точки A. Абсциссу x и ординату y точки A называют координатами точки A.

Координаты точки, записывают в круглых скобках рядом с буквой, обозначающей эту точку: М (х; у).

х – первая координата

у – вторая координата

Поменять местами х и у нельзя – получится другая точка.

Поэтому пару координат (x; y) точки A называют упорядоченной парой чисел.

Если на плоскости задана прямоугольная система координат хOу, то:

– каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);

– разным точкам плоскости соответствуют разные упорядоченные пары чисел;

– каждая упорядоченная пара чисел соответствует одной точке плоскости.

То есть установлено взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.

Алгоритм построения точки на координатной плоскости

Построим точку А(3; 6).

Введём прямоугольную систему координат.

На каждой оси откладываем заданные координаты х и у (x > 0 и y > 0, значит, точка A расположена в I координатной четверти).

Проводим перпендикуляры к оси х и оси у.

Точка их пересечения – искомая точка.

В(– 4; 5) – имеет отрицательную абсциссу и положительную ординату, значит, расположена во II четверти.

С(– 8; – 4) – имеет обе отрицательные координаты, значит, расположена в III четверти.

D(9; – 2) – имеет положительную абсциссу и отрицательную ординату, значит, расположена в IV четверти.

F(6; 0), E(– 5; 0) – точки лежат на оси абсцисс.

H(0; – 5) – точка лежит на оси ординат.

O(0; 0) – начальная точка системы координат.

В географии положение объектов на земной поверхности определяется двумя координатами: широтой и долготой.

В концертном зале своё кресло можно найти по номеру ряда и места.

В шахматах каждой клетке соответствует буква столбца и цифра ряда.

Разбор заданий тренировочного модуля

Тип 1. Ввод с клавиатуры пропущенных элементов в тексте

Построить прямую АВ, если А(3; 2), В(– 3; – 4).

1) координаты точек пересечения прямой AB с осями;

2) координаты середины отрезка AB.

Шаг 1. Строим точки А и В по их координатам.

Шаг 2. Проводим прямую АВ.

Шаг 3. Находим точки пересечения с осями координат, обозначаем их буквами M и N. Определяем их координаты:

Шаг 4. Находим по графику середину отрезка АВ, это точка N (0; – 1).

Ответ: координаты точек пересечения прямой AB с осями: М (1; 0), N (0; – 1), координаты середины отрезка AB: N (0; – 1).

Тип 2. Нарисуйте фигуру, последовательно соединяя точки

(0; 4), (– 2; – 2), (3; 2), (– 3; 2), (2; – 4), (0; 4).

Источник