Что такое периметр окружности

Онлайн калькулятор периметра круга. Как узнать длину круга, окружности.

Что такое длина окружности или периметр круга и как ее вычислить? Для того что бы это понять нам необходимо разобраться с тем чему равна длина окружности.

Длина окружности всегда равна числу π (Пи)

Давайте с вами разберемся что же такое число пи. Π – это постоянная величина равная 3,14159265…

Но обычно Пи приравнивают к 3,14 и это число используют для математических расчетов в которых не требуется оооооооооочень точное вычисление.

Откуда же взялось это число и почему оно всегда равно одному и тому же? Для того что бы нам понять что такое число пи нам необходимо разобрать простой пример. Допустим у нас имеется окружность с диаметром равному единицы, так вот длина окружности — это число «пи».

Иными словами Пи ≈ 3,14 диаметрам круга или окружности.

Теперь зная и понимая что такое π мы можем с легкостью высчитать периметр или длину окружности которая равна

P = D * π
или
P = 2 πR
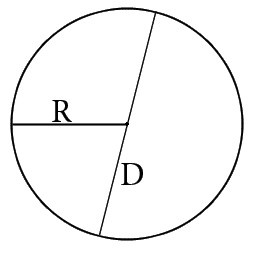
где R –это радиус, а D – это диаметр

Источник

Формула периметра круга

Определение периметра круга

Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(

Формула периметра круга

Периметр круга радиуса \(r\) :

\[ \LARGE

= 2 \cdot \pi \cdot r \]

\( P \) – периметр (длина окружности).

Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки.

Центром окружности будем называть точку, которая задается в рамках определения 1.

Радиусом окружности будем называть расстояние от центра этой окружности до любой ее точки.

По формуле расстояния между двумя точками в заданной нами системе координат, получим:

Таким образом, мы и получаем, что уравнение (1) является уравнением окружности в декартовой системе координат.

Длина окружности (периметр круга)

Тогда, будем получать, что

Получаем, что отношение \( \frac<ρ><ρ'>=\frac<2τ> <2τ'>\) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть

С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \( n→∞ \) ), будем получать равенство:

Из последних двух равенств получим, что

Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть

Окончательно, получим, что длина окружности (периметр круга) определяется формулой

Источник

Длина окружности

6 класс, 9 класс, ЕГЭ/ОГЭ

Как найти длину окружности через диаметр

Диаметр — отрезок, который соединяет две точки окружности и проходит через её центр. Формула длины окружности через диаметр:

π— число пи — математическая константа, равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, равное 3,14

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, равное 3,14

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она всегда равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

Источник

Периметр круга или длина окружности

Отношение длины окружности к её диаметру одинаково для всех окружностей. Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π = 3.14159.

Формула для вычисления длины окружности

Остались вопросы?

Здесь вы найдете ответы.

Периметр круга, также называемый длиной окружности, представляет собой число, получаемое в результате умножения его радиуса на два Пи, либо путем перемножения между собой его диаметра и числа Пи. Формула, используемая для расчета периметра круга, представлена в следующем виде:

π — это величина, которая является константой, выражающей отношение длины окружности к ее диаметру. Ее значение постоянно равно 3,14.

Под определением «расчет периметра круга» подразумевается процедура, направленная на установление длины окружности, ограничивающей его. В случае, когда длина радиуса круга является известной величиной, длина окружности может быть вычислена с применением приведенной ниже формулы:

в ней радиус круга обозначен как r.

Под радиусом окружности подразумевается отрезок, который соединяет центр окружности с любой из множества точек, находящихся на ней.

Значение длины окружности также может быть вычислено, если диаметр круга известен. С этой целью нужно произвести умножение ее диаметра (d) на число Пи (π). В этом случае следует пользоваться формулой:

Если раскрывать такое понятие, как «диаметр окружности», то стоит отметить, что им является отрезок, проходящий через ее центр и соединяющий две любые точки этой окружности.

Число Пи (π) является математической постоянной, рассчитываемой как отношение длины окружности к величине ее диаметра. Оно равно 3,14.

Периметр круга представлен величиной, равной длине окружности, которая ограничивает его. Это значит, что данная величина может быть рассчитана по формуле:

В описанном в задании случае сторона квадрата, в который вписан круг, выступает в роли его диаметра. Это дает основания для расчета периметра круга следующим образом:

P = 20 * 3,14 = 62,8 см.

Ответ: Периметр круга, который вписан в квадрат, имеющий сторону 20 см, равен 62,8 см.

Длина окружности представляет собой произведение, полученное в результате умножения ее диаметра (D) на число Пи (π): L = π*D = 30*π. В данном случае длина окружности – это ее периметр. Из этого следует, что диаметр окружности D равен 30.

Решение поставленной задачи следует начинать с расчета длины первого круга. Для этого число Пи, равное 3,14, нужно умножить на два, а затем полученное значение также умножить на длину радиуса круга. Формула, используемая при этом, выглядит так:

Принимая во внимание тот факт, что диаметр второго круга в три раза превышает диаметр первого из них, то можно с уверенностью говорить о том, что его радиус также будет троекратно превышать радиус первого круга. Это означает, что формула, применяемая для расчета длины второго круга, будет выглядеть так:

Подставив в формулу величины, приведенные в задании, можно получить следующий результат:

Ответ: Длина второго круга равна 10,8 дм.

В задании указано, что площадь круга составляет 25 дм.кв. Это значит, что произведение числа Пи и радиуса круга, возведенного в квадрат, равно 25 дм.кв. Из этого следует, что радиус данного круга равен величине, полученной в результате деления 5 на квадратный корень из числа Пи (r = 5/√π). На основании этого можно сделать вывод о том, что длина круга может быть высчитана по следующей формуле:

В результате получается число, приблизительно равное 17,72 дм.

Ответ: Длина круга равна примерно 17,72 дм.

Формула, которая предназначена для расчета длины круга выглядит так:

По сути, это произведение числа Пи и диаметра круга.

В случае, который описан в задании, длина круга равна 40 Пи см, а это значит следующее:

Число Пи сокращается в обеих частях получившегося уравнения, и в итоге получается, что диаметр круга равен 40 см:

Располагая информацией о длине круга, можно вычислить его радиус. Это можно сделать на основании приведенной ниже формулы:

r = L/(2*π) = 19,1:(2*3,14)=3 м.

Таким образом удалось установить, что радиус круга равен 3 м.

Теперь, зная длину радиуса круга, можно произвести расчет его площади по формуле:

π*r2 = 3,14*3*3 = 28,26 м².

Ответ: Площадь круга равна 28,26 м. кв.

При расчете таких показателей, как площадь и диаметр круга, следует использовать его длину. Она обозначается как с и равна 26 см. Согласно формуле вычисления длины круга, она равна произведению 2 Пи и радиуса круга, либо Пи и его диаметра (с=2πr или c=πd). Исходя из этого, диаметр круга можно найти путем деления длины круга на число Пи:

В данном случае d=26/3,14=8,28 см.

Теперь, когда все необходимые для вычисления площади круга параметры известны, можно перейти непосредственно к ее расчету:

В целях выполнения вычисления длины окружности по радиусу (r) следует произвести умножение величины, выражающей его значение, на два Пи. При этом используется следующая формула:

При расчете длины окружности используется формула, которая имеет следующий вид:

Согласно данной формуле, для того чтобы вычислить, чему равна длина окружности, необходимо произвести умножение ее диаметра на число Пи, равное 3,14.

Подставляя в приведенную выше формулу числа, указанные в задании, можно произвести расчет длины окружности, которая будет равна:

Ответ: Длина окружности диаметром в 4 м равна 12,56 м.

Площадь круга высчитывается при помощи формулы:

В данном конкретном случае указано, что площадь равна Пи м. кв. (S=π).

Исходя из вышеизложенного, можно произвести расчет величины радиуса, которая будет равна отношению корня квадратного из числа Пи и числа Пи:

Теперь можно приступить к вычислению непосредственно длины окружности, используя следующую формулу:

Ответ: Длина окружности круга площадью Пи кв. м равна 2 Пи.

При расчете длины круга следует брать за основу формулу, которая предполагает умножения числа Пи, равного 3,14, на диаметр окружности круга. Если говорить о конкретном случае, упомянутом в задании, то расчет длины окружности будет выглядеть следующим образом:

Ответ: Длина круга, диаметр которого равен 16 см, составляет 50,24 см.

Длина окружности рассчитывается с применением формулы, составными элементами которой являются диаметр (d) и число ПИ, равное 3,14. Для вычисления длины окружности упомянутые величины следует перемножить:

Ответ: Круг диаметром 5,8 дм имеет длину окружности, равную 18,212 дм.

Если диаметр круга является известной величиной, то ее вполне достаточно, для того чтобы произвести расчет длины данного круга. С этой целью следует использовать формулу, приведенную ниже:

Если подставить в данную формулу величины, заданные в вопросе, то можно получить следующий результат:

Ответ: Длина круга, диаметр которого равен 18 м, составляет 56,52 м.

Источник

Способы расчета периметра круга и длины окружности

Периметр круга — что это, определение

Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.

Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.

Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.

Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.

Периметр — это длина окружности, ограничивающей круг.

Понятия «периметр круга» и «длина окружности» считаются синонимичными.

Как рассчитать периметр круга или длину окружности

Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159. \)

Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:

Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.

Через радиус

Длину окружности L можно найти по формуле через радиус:

где \(\pi \) — число Пи, R — радиус.

Через диаметр

Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:

Примеры решения задач

Задача

Каков периметр круга, если его радиус равен 0,5 см?

Решение

Задача

Какова длина окружности, если ее диаметр равен 2 см?

Источник