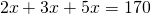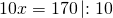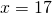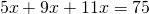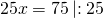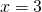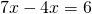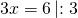Как поделить число на части

Пропорциональное деление

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.

Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:

Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.

90 : (1 + 2 + 3) = 90 : 6 = 15;

Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.

Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:

значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то

Второй способ: обозначим искомые части буквами a, b и c:

Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:

Следовательно, c равно:

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

так как 15 + 10 + 8 = 33, то

Деление на части, обратно пропорциональные числам

Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как

Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

Источник

Как разделить число в отношении

Как разделить число на части в данном отношении? Рассмотрим, как это сделать, на конкретных примерах.

1) Разделить число 170 на три части в отношении 2:3:5.

1)2+3+5=10 (частей) составляет все число.

2)170:10=17 — приходится на одну часть.

3)2∙17=34 — величина I части.

4)3∙17=51 — величина II части.

5)5∙17=85 — величина III части.

Пусть х — величина одной части. Поскольку мы делим число на пропорциональные части, величину одной части называют коэффициентом пропорциональности. Поэтому чаще всего сражу же пишут: пусть х — коэффициент пропорциональности. Тогда I часть равна 2х, II — 3х, III — 5х. Сумма трех частей равна числу:

Значит, I часть равна 2∙17=34, 3∙17=51, II — 3∙17=51, III — 5∙17=85.

2) Периметр треугольника равен 75 см, а стороны относятся как 5:9:11. Найти стороны треугольника.

Пусть х- коэффициент пропорциональности. Тогда стороны треугольника равны 5 см, 9х см и 11х см. По условию, периметр треугольника равен 75 см. Составим и решим уравнение:

Следовательно, стороны треугольника равны 5∙3=15 см, 9∙3=27 см, 11∙3=33 см.

Ответ: 15 см, 27 см, 33 см.

3) Настя и Лиза поделили конфеты в отношении 4:7. При этом у Лизы оказалось на 6 конфет больше. Сколько конфет было всего?

Пусть х — коэффициент пропорциональности. Тогда Насте досталось 4х конфет, Лизе — 7х конфет. Так как у Лизы конфет на 6 больше, чем у Насти, составляем уравнение:

Значит, количество конфет Насти 4∙2=8, Лизы — 7∙2=14, а всего у них 8+14=22 конфеты.

4 Comments

Решение последней (3й) задачи следует поправить, так в ней спрашивается общее количество конфет — 22.

Геннадий, спасибо, исправила.

Наверное, отношение стоимости 5 ручек к стоимости 4 тетрадей. 5 ручек стоят 5∙40=200 рублей, 4 тетради — 4∙70=280 рублей. Следовательно, отношение стоимости 5 ручек к стоимости 4 тетрадей равно 200/280=5/7.

Источник

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Деление натуральных чисел

Подобно тому, как вычитание является обратным действием для сложения, так и для умножения существует свое обратное арифметическое действие.

Рассмотрим задачу. В школьной столовой раздали 90 яблок по 3 яблока каждому ученику класса. Сколько учеников учатся в этом классе?

Если бы нам было известно количество учеников в классе и количество яблок, которое получил каждый из них, то общее число яблок мы узнали бы, умножив число учеников на число яблок, доставшееся каждому. То есть, количество учеников – это первый сомножитель, количество яблок – второй сомножитель, а сколько яблок раздали – это произведение.

Деление – это арифметическое действие, которое состоит в нахождении одного из сомножителей при помощи данного произведения и второго сомножителя.

Делимое – это число, которое мы делим на другое. Это то самое произведение, которое нам дано.

Делитель – это число, на которое мы делим делимое. Это данный нам один из множителей.

Частное – это результат действия деление, то есть, искомый нами второй сомножитель.

На записи действие деление обозначается: двоеточием ( \(\textcolor <:>\) ), знаком обелюс ( \(\textcolor <\div>\) ), горизонтальной чертой или косой чертой ( \(\textcolor \) ).

Так, решение нашей задачи можно записать следующими способами:

При записи от руки действие деление принято записывать в виде двоеточия, обелюс применяется в печатной литературе, косая черта, которая по-другому называется слеш, – при записи на компьютере, а горизонтальная черта используется при записи деления в виде обыкновенной дроби.

Итак, разделить число a на число b – это значит найти такое число c, которое при умножении его на число b дает в результате числа a.
То есть: \(\textcolor \) , если \(\textcolor \) .

Компоненты действия деление:

Деление с остатком и неполное частное

К примеру, если мы захотим раздать все 37 яблок поровну между пятью детьми, то у нас это сделать не получится. Мы сможем раздать (использовать из всего количества яблок) только по 7 яблок каждому ( \(\textcolor <7\cdot 5=35>\) ), и у нас останется 2 яблока ( \(\textcolor <37-35=2>\) ).

Итак, деление с остатком – это нахождение такого наибольшего целого числа, умножив которое на делитель, мы получим число, максимально близкое к делимому, но не превосходящее его. Это искомое число называется неполное частное. Разница между делимым и неполным частным называется остаток.

Остаток всегда меньше делителя!

Связь деления с умножением, сложением и вычитанием

Когда мы выполняем находим произведение двух чисел, эти числа нам известны, а от нас требуется найти результат действия умножение. При делении (без остатка) нам известно произведение двух чисел, а найти нужно такое число, которое при умножении на известное данное число дает это самое произведение.

Следовательно, действие деление является обратным действию умножения.

Справедливо также и обратное, что действие умножение обратно действию деления. Таким образом:

Умножение и деление – это взаимно обратные действия.

Связь деления с умножением, а также со сложением и вычитанием прекрасно видна, если рассмотреть, как с помощью этих действий можно выполнить действие деление.

Деление двух чисел при помощи сложения

Деление двух чисел при помощи вычитания

То есть, 69 от 345 можно отнять 5 раз, поэтому \(\textcolor <349\div 69=5>\).

Деление двух чисел при помощи умножения

При помощи умножения узнать ответ на наш вопрос можно перебирая множитель числа 69 до тех пор, пока не получим заданное нам 345 :

Но эти три способа очень громоздки, особенно если частное представляет собой очень большое число. Их нужно знать только для того, чтобы понимать суть действия деления, суть тех задач, которые решаются посредством него.

Общий принцип деления в столбик

Если частное от деления двух чисел является многозначным числом, нахождение его происходит путем деления в столбик. Еще его называют деление уголком.

Прежде всего, нужно узнать количество цифр в частном и первое неполное делимое; как их находить, я подробно расписал в этой статье. В нашем случае первое неполное делимое равно 295 тысяч, а в частном будет 4 цифры.

Далее записываем известные компоненты деления следующим образом:

и начинаем вычисление:

1. Берем первое неполное делимое и пытаемся его разделить на делитель.

Вот тут нам и пригодится способ нахождения однозначного частного. Воспользовавшись им, находим, что в 295 тысячах делитель 34 содержится целиком 8 тысяч раз.

Записываем в частное первую найденную цифру разряда тысяч, а под неполным делимым пишем результат произведения неполного частного и делителя. И сразу же находим остаток от этого действия, т.е. вычитаем из неполного частного результат этого произведения.

В результате умножения первой найденной цифры частного на делитель у нас получилось \(\textcolor <8\cdot 37=272>\). Записываем его под 295 и находим разницу: \(\textcolor <295-272=23>\). Значит, 23 тысячи у нас остаются неразделенными.

В качестве еще одного действия самопроверки нужно сравнить полученную разницу с делителем. Если она меньше делителя, то мы на правильном пути, если же разница равна или больше делителя, то мы или неправильно нашли цифру частного, или допустили ошибку при умножении на делитель либо при нахождении остатка.

2. Оставшиеся неразделенные 23 тысячи представляют собой 230 сотен. Прибавляем к ним те 3 сотни, которые содержатся в делимом (говорят: сносим пять) и получаем второе неполное делимое 233 сотни.

3. 29 неразделенных сотен – это 290 десятков. Добавляем (сносим) к ним 8 десятков делимого, получаем третье неполное делимое 298 десятков.

4. И наконец, 26 десятков – это 260 простых единиц. Добавляем (сносим) к ним 3 единицы делимого и получаем четвертое неполное делимое 263 единицы.

Рассмотрим еще один пример. \(\textcolor <25326\div 63>\).

1 сотня = 10 десятков, добавляем (сносим) 2 десятка из делимого, получаем второе неполное делимое 12 десятков.

Итак, запомните, что каждое неполное делимое образует в частном одну цифру соответствующего разряда и что даже если неполное делимое меньше делителя, то в частном все равно нужно записать нулевой результат этого действия.

Итак, в общем виде алгоритм деления в столбик выглядит так:
1. Находим первое неполное делимое и количество цифр в частном.
2. Делим неполное делимое на делитель. Цифру, полученную в результате деления записываем ниже черты под делителем.
3. Умножаем полученную цифру на делитель, результат записываем под неполным делимым.
4. Ставим между ними знак минус и выполняем действие.
5. К полученной разнице сносим цифру следующего разряда (если она есть) и получаем второе неполное делимое.
6. Выполняем пункты 2-5 до тех пор, пока в делимом не останется ни одной неснесенной цифры.
7. Если неполное делимое невозможно разделить на делитель, то в частном ставится 0 и к этому неполному делимому сносится следующая цифра.

Деление на числа, заканчивающиеся нулями

Как и в случае с умножением, деление чисел облегчается, если делитель заканчивается одним или несколькими нулями. Рассмотрим два возможных случая:

Рассмотрим первый случай.

Деление на единицу с любым количеством нулей

Единица с любым количеством нулей – это не что иное как единица соответствующего разряда. Например, 10 – это 1 единица разряда десятков, 1000 – это одна единица разряда тысяч, 10000000 – 1 единица разряда десятков миллионов и т.д.

Запишите:
Чтобы разделить какое-нибудь число на единицу с любым количеством нулей, нужно отсчитать в делимом справа столько цифр, сколько нулей содержится в делителе; тогда все цифры, находящиеся слева от разделения, составят частное, а те, что справа – будут остатком.

Деление на число, оканчивающееся нулями

Рассмотрим на примере \(\textcolor <284556\div 2800>\).

Делитель здесь не что иное как 28 сотен. Логично предположить, что эти 28 сотен могут хотя бы один раз содержаться только в сотнях делимого. Значит, нам нужно определить, сколько в делимом всего единиц разряда сотен, и разделить их на 28 единиц разряда сотен делимого. А отброшенные цифры десятков и простых единиц добавятся к остатку.

Запишите:
Чтобы разделить какое-нибудь число на число, заканчивающееся нулями, нужно отбросить мысленно нули в делителе, в делимом тоже отбросить мысленно такое же количество цифр, как и нулей в делителе. Получившееся число в делимом разделить на получившееся число в делителе, а к остатку прибавить (снести) те цифры делимого, которые отбросили ранее.

Проверка деления

Так как делимое – это делитель, умноженный на частное и плюс остаток, что следует из определения деления, то результат выполнения деления можно проверить умножением.

Если в результате действия деления не получилось остатка, то деление можно проверить и делением. Действительно, если делимое – это произведение делителя и частного, то разделив делимое на частное (один из сомножителей), мы должны получить второй сомножитель, то есть, делитель.

Свойства деления

Свойства деления я представлю двумя группами:

Давайте рассмотрим каждую группу подробнее.

Действия деления с единицей и нулем

При делении числа на единицу получается то же самое число.

Действительно, разделить число на единицу означает узнать, сколько единиц содержится в данном числе. А количество единиц в числе – это не что иное, как само это число.

И ли вот, например, если 10 яблок нужно раздать одному человеку ( 10 поделить на 1 ), то ему все эти 10 яблок и достанутся, правда?

При деление одинаковых чисел (числа на равное число) в результате будет 1 (единица).

В самом деле, если все единицы какого-то числа разделить на количество частей, равное количеству единиц этого числа, то в каждая часть получит по 1 единице.

Например, если 20 яблок раздать 20 школьникам, то каждому достанется по 1 яблоку.

При делении нуля на любое число, отличное от нуля, в результате будет нуль.

Разделить нуль на число означает найти такое число, умножив которое на данный делитель, мы получим в результате нуль. А такое число только одно – это нуль.

На нуль делить нельзя, то есть, нуль не может выступать в роли делителя.

При делении каких угодно чисел делителем может быть любое число, кроме нуля.

Рассмотрим два случая: когда нулём является только делитель, и когда делимое и делитель оба нули.

Распределительные свойства деления

Чтобы найти частное от деления суммы на число, нужно поделить каждое слагаемое на это число, и найти сумму полученных частных.
\(\textcolor <(a+b+c)\div d=a\div d+b\div d+c\div d>\).
При этом подразумевается, что все действия деления получаются без остатка.

Чтобы найти частное от деления разности на число, нужно поделить на это число отдельно сперва уменьшаемое, а потом вычитаемое, после чего найти разность первого частного и второго.
\(\textcolor <(a-b)\div c=a\div c-b\div c>\)
При этом также предполагается, что при делениях уменьшаемого и вычитаемого на число не получается остатков.

Например: \[\textcolor <(36-24)\div 6=36\div 6-24\div 6=6-4=2>\] Число 36 состоит из 6 шестерок, а 24 – из 4 шестерок, а забрав у 6 шестерок 4 шестерки, получим 2 шестерки. Такой же итог будет и если мы сперва у 36 отнимем 24 единицы (останется 12 ), а потом найдем, сколько в этой разнице содержится шестерок: \(\textcolor <12\div 6=2>\).

Чтобы найти частное от деления произведения на число, нужно поделить на него только один из сомножителей, а результат умножить на неизмененные остальные.
\(\textcolor <(a\cdot b\cdot c)\div d=a\div d\cdot b\cdot c=b\div d\cdot a\cdot c=c\div d\cdot a\cdot b>\).

Чтобы найти частное от деления числа на произведение, нужно это число поделить на первый сомножитель, результат деления поделить на второй сомножитель, полученное частное – на третий и так далее.
\(\textcolor \).
При этом предполагается, что при всех этих делениях не получается остатков.

На рисунке наглядно видно, что в итоге после применения этого правила, число 30 получилось разделенным на 6 равных частей.

Изменение частного при изменении делимого и делителя

При рассмотрении изменений частного в результате изменений делимого и делителя предполагается, что действие деление происходит без остатка. В противном случае изменения могут быть не такими, о которых идет речь ниже.

При увеличении делимого в определенное количество раз, частное увеличится в это же количество раз, а при уменьшении – уменьшится.

Если мы в примере \(\textcolor <24\div 4=6>\) делимое увеличим, к примеру, в 3 раза, то мы можем переписать это выражение в виде \(\textcolor <(24+24+24)\div 4>\). Используя свойство деления суммы на число, мы увидим, что теперь нам нужно сложить три слагаемых, каждое из которых равно начальному выражению: \(\textcolor <24\div 4+24\div 4+24\div4>\). Отсюда очевидно, что результат будет больше начального в 3 раза.

Если мы в этом же примере \(\textcolor <24\div 6>\) уменьшим делимое в 3 раза, то есть, разделим его на три равные части, то очевидно, что результат деления одной части на 6 будет в 3 раза меньше, чем результат деления трех таких же частей. Посмотрите сами. Начальное выражение \(\textcolor <24\div 6>\) можно записать в виде: \(\textcolor <(8+8+8)\div 6=8\div 6+8\div 6+8\div 6>\), а уменьшенное в 3 раза делимое даст нам только одно из трех таких слагаемых: \(\textcolor <8\div 6>\).

При увеличении делителя в определенное количество раз, частное уменьшится в это же количество раз, а при уменьшении – увеличится.

Действительно, изменение делителя означает, что делимое необходимо разделить на большее или меньшее количество равных частей. Соответственно, если нужно разделить на большее число частей, то каждая часть будет меньше, чем изначально, а если делить на меньшее число частей, то каждая часть будет крупнее.

В случае одновременного изменения делимого и делителя, частное может вести себя по-разному, или же вообще оставаться без изменений. Если нужно узнать, станет оно больше или меньше, нужно сперва посмотреть, как частное изменится после изменения делимого, а потом – как изменится после изменения делителя.

При увеличении или уменьшении делимого и делителя в одинаковое количество раз, частное не меняется.

Попробуйте самостоятельно доказать справедливость этого утверждения. Пишите в комментариях, получилось это, или нет.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 3.7 / 5. Количество оценок: 3

Источник