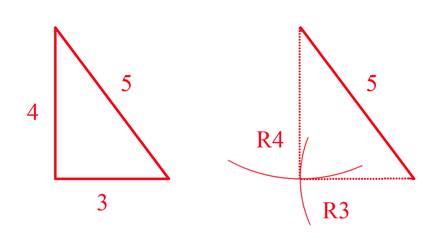Как поделить отрезок пополам циркулем

Деление отрезка пополам при помощи циркуля

Имеется отрезок произвольной длины. Необходимо разделить его пополам, пользуясь только циркулем и не прибегая к помощи линейки.

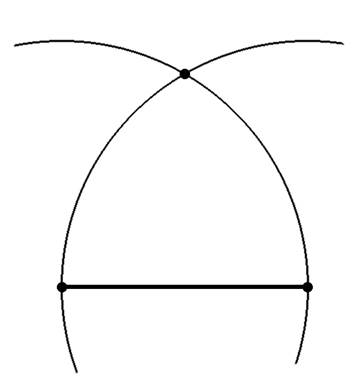
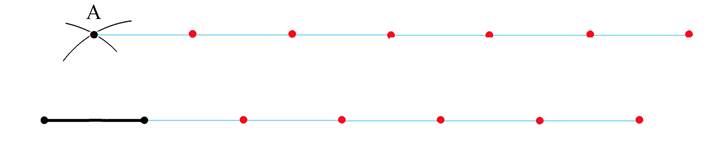
По сути, всё, что можно сделать сначала – это прочертить

Из концов отрезка две окружности радиусом равным длине отрезка.

Концы отрезка и точка пересечения окружностей образуют

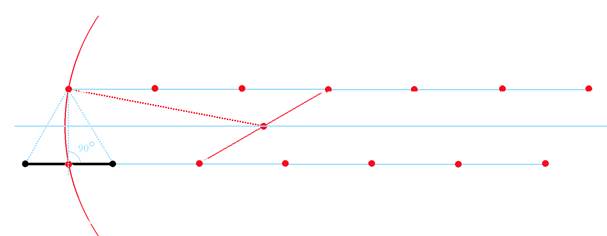
Пользуясь этим методом можно построить сетку из вспомогательных точек сколь угодно большого размера. Нам потребуется всего два ряда точек лежащие на прямой, являющейся продолжением отрезка и параллельной ей прямой проходящей через вершину построенного нами первого треугольника.

В равностороннем треугольнике любая высота (перпендикуляр, проведенный из вершины к противоположной стороне) является одновременно медианой (линией соединяющей вершину и середину противоположной стороны) а значит, чтобы получить

середину отрезка, достаточно провести через вершину треугольника окружность, центр которой лежит на прямой, равноудаленной от прямой, являющейся продолжением исходного отрезка и параллельной ей прямой проходящей через вершину треугольника. Центром окружности может служить середина отрезка, концы которого расположены на вышеупомянутых прямых

Но, по условию задачи, пользоваться линейкой мы не можем

(все линии на рисунках начерчены лишь для пояснения), а значит

в окончательном построении нам придется пользоваться лишь точками из верхнего и нижнего рядов или точкой из верхнего ряда и точкой лежащей на исходном отрезке. Концы вспомогательного отрезка соединить линией мы тоже не сможем, поэтому его центр нам придется получать тоже с помощью единственно циркуля.

Тут нам на помощь придет теорема Пифагора, а точнее её частный случай со сторонами треугольника 3,4 и 5.Угол между сторонами

3 и 4 – прямой, и, следовательно, если мы возьмем отрезок, равный

5 и из одного конца прочертим окружность радиусом 3, а из другого радиусом 4, получим прямоугольный треугольник.

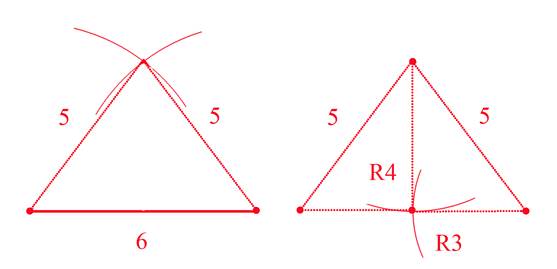
И как следствие мы можем, зная это, получить середину отрезка длиной 6, пользуясь только циркулем.

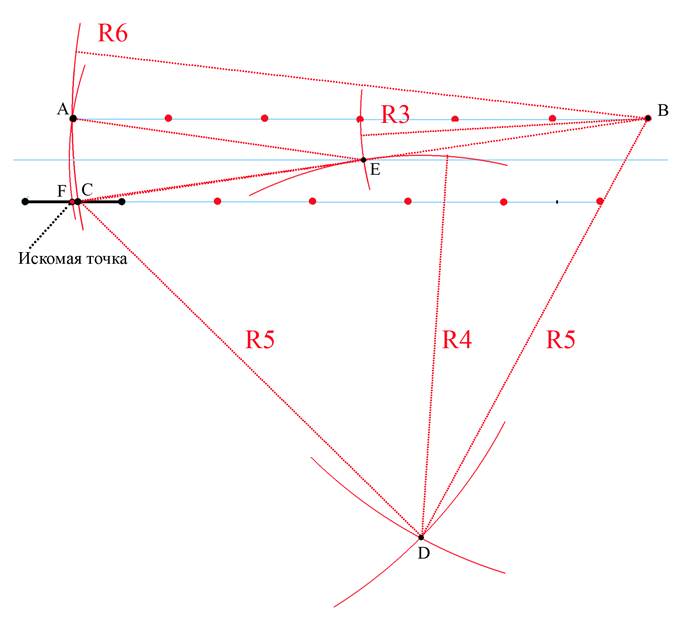
Применив эти построения к нашему случаю, получим такую методу:

1.Проведя из концов исходного отрезка дуги окружностей радиусом

равным длине отрезка получим на их пересечении точку A– вершину равностороннего треугольника.

2.Сходным образом построим два ряда точек, обозначенных на

рисунке красным. Расстояние между двумя соседними точками равно длине исходного отрезка – условной единице. Точки верхнего ряда лежат на одной прямой и нижнего ряда – аналогично.

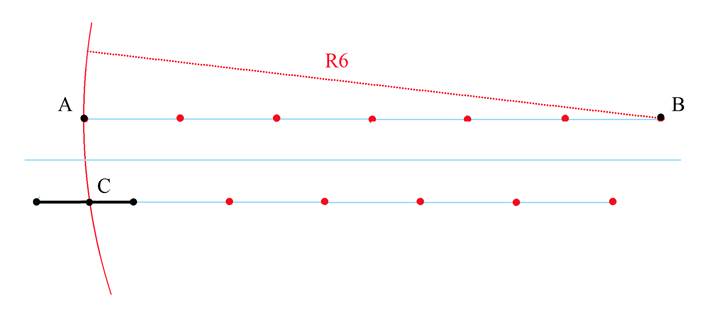
3.Отсчитав от точки А шестую точку, обозначим ее B.

Из точки B проведем дугу окружности радиусом BA= 6

На пересечении этой дуги с исходным отрезком отметим точку C.

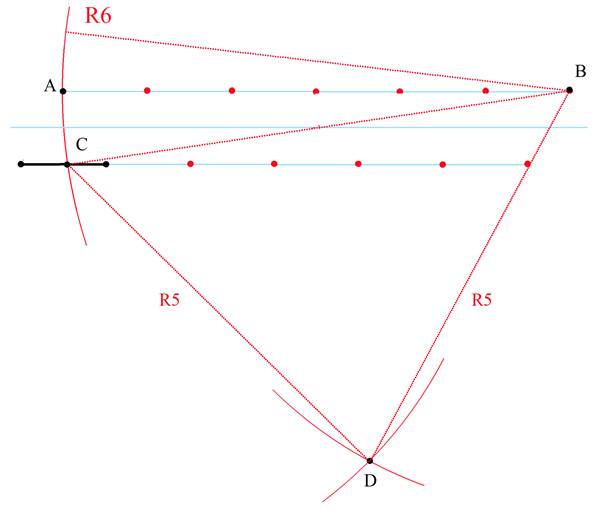
4.Отложим от точки В пять точек и этим радиусом проведем дугу окружности. Этим же радиусом проведем дугу из точки С.

Точку пересечения этих дуг обозначим D.

DC=DB, треугольник CDB – равнобедренный

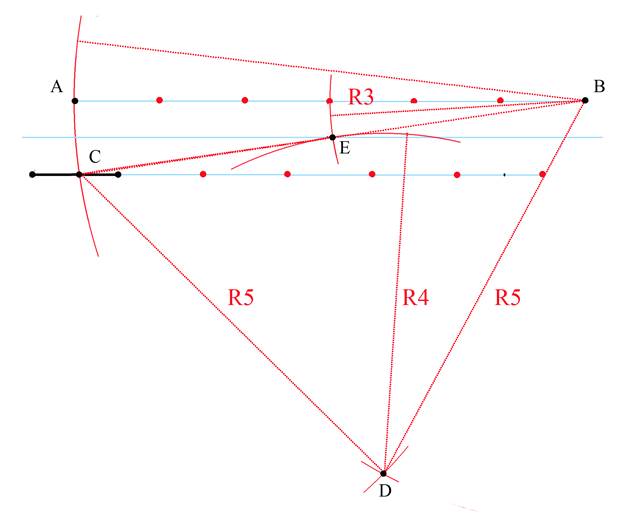
5. Из точки В проведем дугу радиусом 3 а из точки D радиусом 4.

На пересечении дуг получим точку Е – середину отрезка ВС.

Как мы ранее обосновали, точка Е, являясь серединой отрезка ВС,

а значит равноудалена от точки А и искомой точки, являющейся серединой исходного отрезка. Следовательно, приняв ее за центр

и проведя окружность через точку А, на пересечении этой окружности с исходным отрезком получим искомую точку.

6. Что мы и сделаем.

Точка F и есть искомая точка – середина исходного отрезка

Таким образом, задача деления отрезка пополам решается при помощи одного лишь циркуля.

Это станет видно, когда мы уберем из рисунка вспомогательные лини, с помощью которых иллюстрировалось объяснение и

покажем окружности, использовавшиеся для построения промежуточных точек, ранее не показанные, чтобы не отвлекать от объяснения.

Источник

Мастерство не пропьёшь

Головоломки и задачи на сообразительность

понедельник, 21 марта 2011 г.

Деление отрезка пополам

Вот и первая задача в этом блоге.

Все мы с детского садика знаем, как разделить отрезок на две равные части с помощью циркуля и линейки. А вот как разделить отрезок пополам, пользуясь ТОЛЬКО циркулем (без линейки)?

Решение
Дан отрезок AB, требуется разделить его пополам с помощью циркуля.

Построение
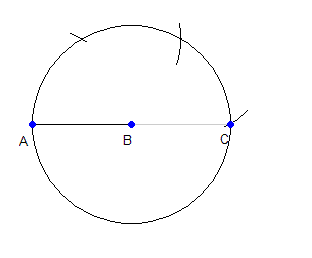
Шаг 1. Проведём окружность радиуса AB с центром в точке B. Тем же раствором циркуля отмерим на этой окружности три дуги, начиная от точки A. Получим точку C.

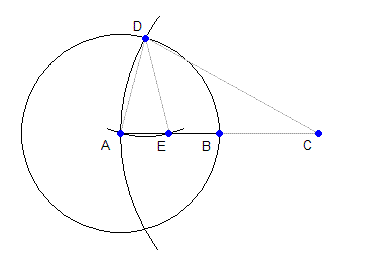
Шаг 2. Проведём окружность радиуса AB с центром в точке A и окружность радиуса AC с центром в точке C. Одну из точек пересечения этих окружностей обозначим D.

Шаг 3. Проведём окружность радиуса AB с центром в точке D. Она пересечёт отрезок AB в точках A и E, причём точка E делит отрезок AB пополам.

Доказательство
Очевидно, что точка C лежит на прямой AB, причём AB=BC, т.е. AC=2*AB

Запишем отношения сторон: AE/AD = AD/AC, следовательно AE = AD*AD/AC = AB*AB / (2*AB) = AB/2.

Этим методом можно делить отрезок не только на 2, но и на N частей. Более того, с незначительными модификациями этот метод применим в случае, когда исходный отрезок вообще не проведён (т.е. заданы только его концы).

Источник

Два одинаковых значения

Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.

При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.

Получение четырех частей

В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.

Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.

Разложение при помощи циркуля

Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:

И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.

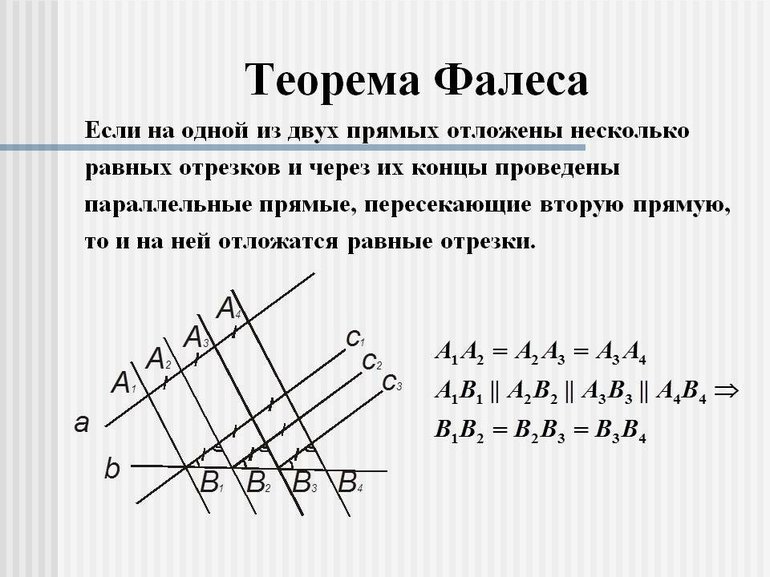
Теорема Фалеса

Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.

Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.

Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.

Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия:

Все эти знания важны в машиностроении при вычерчивании деталей, а также активно применяются в инженерных работах.

Источник

Как разделить отрезок на равные части — формулы и способы

Два одинаковых значения

Самый простой способ разделить на две равнозначные доли — воспользоваться линейкой. Необходимо отмерить общую длину от точки А до точки В и разделить это значение на два. Полученное число следует отметить на заданном интервале, совместив отметку 0 на линейке с точкой А.

При делении на две идентичные доли можно воспользоваться циркулем. Для начала надо отмерить расстояние, которое будет несколько больше, чем предполагаемая половина исходной линии. Чертим две окружности, радиус которых мы определили циркулем. Одну окружность проводим из точки А, а другую — из В. Обе эти окружности между собой соединяются, образуя новые точки — С и D. Потом с помощью линейки и карандаша следует провести линию, соединяющую точки C и D. В том месте, где линия пересекает отрезок, образуется точка Е, которая является центром, а соответственно и делит его пополам.

Получение четырех частей

В таком варианте деления можно в упрощённом виде воспользоваться линейкой. Здесь последовательно сначала отмеряется середина, то есть отрезок делится на две равные части, как указывалось выше, а затем каждый из осечённых секторов по отдельности разделяется пополам. Таким образом, получаются четыре равных отрезка.

Однако такой вариант оказывается удачным лишь на тех прямых, которые имеют целое числовое значение. Здесь следует воспользоваться циркулем.

Разложение при помощи циркуля

Как и в первом описании, при помощи черчения двух окружностей заданный отрезок следует поделить пополам. Таким образом, на прямой образуется два отрезка — АЕ и ЕВ. Далее следует совершить аналогичные действия, но уже с двумя отрезками по отдельности. То есть, взяв отрезок АЕ, провести две окружности:

И снова в местах соединения этих двух дуг нужно провести прямую линию. Тот же самый алгоритм применяется и в отношении линии ЕВ. После проведённых манипуляций отрезок будет пересечён тремя перпендикулярными прямыми, а соответственно, разделён на четыре равные части.

Теорема Фалеса

Если с делением на две или четыре равные части всё более или менее понятно, то деление отрезка на n равных частей вызывает определённые трудности. Здесь приходит на помощь формула параллельных прямых, описанная в теореме Фалеса.

Суть теоремы состоит в том, что при отложении одинаковых отрезков на одной прямой и проведении через концы этих отрезков параллельных прямых, пересекающих другую прямую, то и на второй прямой будут отложены равные между собой отрезки.

Например, на определённой прямой необходимо отмерить пять одинаковых отрезков. Для начала из точки А следует провести прямую линию, которая будет направлена в сторону противоположного конца отрезка (точки В) под острым углом относительно исходной прямой. Теперь при помощи циркуля на этой линии следует отложить пять равных отрезков. Из точки, отмерившей последний отсек, следует очертить линию в точку В. Затем провести прямые, параллельные той, которая проходит через точку В. Каждая линия должна проходить через отмеченные циркулем точки. При условии, что все линии будут строго параллельны друг другу, на исходной прямой будет отложено пять равных отрезков.

Зная, как производить деление на одинаковые части, можно, например, понять, как разделить треугольник на 4 равные части или более. По указанным вариантам деления на сегменты можно производить следующие действия:

Все эти знания важны в машиностроении при вычерчивании деталей, а также активно применяются в инженерных работах.

Источник

Урок геометрии «Элементарные построения. Деление отрезка пополам». 7-й класс

Разделы: Математика

Класс: 7

Для проведения урока по геометрии в 7 классе по теме «Элементарные построения» использовались модели чертёжника, деления отрезка пополам, построения перпендикулярной прямой из цифрового образовательного ресурса «Открытая математика. Планиметрия».

Интерактивный геометрический Чертеж может использоваться в курсе для показа решения задач шаг за шагом, для демонстрации роликов геометрических построений, для решения задач на построение. Наконец, он используется и как отдельное приложение для построения чертежей, которое может быть вызвано из главного меню программы.

Все инструменты, с помощью которых выполняются геометрические построения, встроены в общее окно Чертежа. Для включения любого инструмента нужно нажать на него мышью. Некоторые инструменты также имеют свои собственные панели настроек.

Необходимо отметить, что все эти модели можно установить отдельным файлом на компьютер, и в данном случае обращение к диску будет необязательным.

Конспект учебного занятия

Предмет: Геометрия. 7 класс.

Номер урока по теме: 1

Форма урока: Урок изучения нового материала. Практическая работа.

Цель: Рассмотреть алгоритм основных задач на построение с помощью циркуля и линейки: деление отрезка пополам, построение перпендикуляра к данной прямой.

Ожидаемые результаты: Выполнение практических работ с помощью циркуля и линейки: деление отрезка пополам, построение перпендикуляра к данной прямой.

Этапы урока с временной раскладкой:

I. Организационный момент.

Проверка готовности учащихся к уроку.

На дом учащимся были заданы задачи на готовых чертежах, необходимо было найти на чертеже равные треугольники и доказать их равенство.

Цель этого этапа: обучающий контроль.

Какие теоремы мы применяли при решении задач? (Первый, второй и третий признаки равенства треугольников)

Цель: повторение с проговариванием признаков равенства треугольников, пропедевтика темы «Подобие».

Но кроме изученных этих трёх теорем на предыдущих уроках мы познакомились с определением и свойствами равнобедренного треугольника.

Вашему вниманию предлагается следующее: определить, является ли треугольник равнобедренным?

Цель: повторить определение и свойства равнобедренного треугольника.

Примечание: в случае, если вы чувствуете нехватку времени, количество устных задач можно уменьшить (именно для этого они перечисляются не все подряд, а предлагаются в виде гиперссылок).

Цель: ещё раз наглядно, без проговаривания, повторить в назывном порядке признаки равенства треугольников, определение и свойства равнобедренного треугольника.

III. Изучение нового материала.

Тема сегодняшнего урока: деление отрезка пополам.

Как можно разделить отрезок пополам?

Цель: повторить деление отрезка пополам с помощью линейки.

К объявленной теме я добавляю слова: «с помощью циркуля и линейки». Цель нашего урока: рассмотреть и доказать алгоритм задачи на построение с помощью циркуля и линейки: деление отрезка пополам.

Цель: объявление темы и цели урока.

Этот алгоритм рассмотрим на модели. Внимание на экран.

Деление отрезка пополам / construction1 можно включить и на ученических компьютерах.

Примечание: этап анализа решения задачи перед этапом построения в 7-ом классе не проводится.

Цель: разобрать алгоритм деления отрезка пополам.

Докажем, что точка О делит отрезок АВ пополам.

Цель: исследовать задачу деления отрезка пополам на количество решений.

Примечание: исследование на количество точек-середин у отрезка проводится на интуитивном уровне, строгого доказательства учащимся 7-го класса не предлагается.

V. Первичное закрепление.

После отдыха самостоятельно с помощью чертёжника разделите отрезок пополам. При затруднении обратитесь к алгоритму.

Цель: самостоятельное выполнение практической работы в группах.

Обратимся к полученному чертежу. Прямая СС₁ не только делит отрезок АВ пополам, но и проходит перпендикулярно к нему.

Отсюда и вытекает алгоритм построения прямой, перпендикулярной к данной.

Цель: разбор алгоритма и построение прямой, перпендикулярной к данной (доказательство следует из предыдущего пункта).

Но строили мы прямую, перпендикулярную к данной, через точку, лежащую на прямой. Но ведь точка может и не принадлежать прямой. Отсюда и следует ваше домашнее задание.

Источник