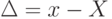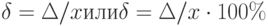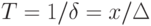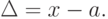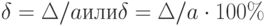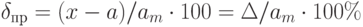Как подразделяются погрешности по характеру проявления
Погрешность
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
Классификация погрешностей
По форме представления
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
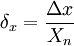
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
По причине возникновения
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Классификация. Погрешность измерений
Эффективность использования измерительной информации зависит от точности измерений — свойства, отражающего близость результатов измерений к истинным значениям измеренных величин. Точность измерений может быть большей или меньшей, в зависимости от выделенных ресурсов (затрат на средства измерений, проведение измерений, стабилизацию внешних условий и т. д.). Очевидно, что она должна быть оптимальной: достаточной для выполнения поставленной задачи, но не более, ибо дальнейшее повышение точности приведет к неоправданным финансовым затратам. Поэтому наряду с точностью часто употребляют понятие достоверность результатов измерений, под которой понимают то, что результаты измерений имеют точность, достаточную для решения поставленной задачи (погрешность измерений).
Классический подход к оцениванию точности измерений, впервые примененный великим математиком Карлом Гауссом и затем развитый многими поколениями математиков и метрологов, может быть представлен в виде следующей последовательности утверждений.
1. Целью измерения является нахождение истинного значения величины — значения, которое идеальным образом характеризовало бы в качественном и количественном отношении измеряемую величину. Однако истинное значение величины найти в принципе невозможно. Но не потому, что оно не существует — любая физическая величина, присущая конкретному объекту материального мира, имеет вполне определенный размер, отношение которого к единице является истинным значением этой величины. Это означает всего лишь непознаваемость истинного значения величины, в гносеологическом смысле являющегося аналогом абсолютной истины. Хорошим примером, подтверждающим это положение, являются фундаментальные физические константы (ФФК).
Они измеряются наиболее авторитетными научными лабораториями мира с наивысшей точностью, и затем результаты, полученные разными лабораториями, согласуются между собой. При этом согласованные значения ФФК устанавливают с таким количеством значащих цифр, чтобы при следующем уточнении изменение произошло в последней значащей цифре. Таким образом, истинные значения ФФК неизвестны, но каждое следующее уточнение приближает значение этой константы, принятое мировым сообществом, к ее истинному значению.
I la практике вместо истинного значения используют действительное значение величины — значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
2. Отклонение результата измерения X от истинного значения Хи (действительного значения Хд) величины называется погрешностью измерений

Вследствие несовершенства применяемых методов и средств измерений, нестабильности условий измерений и других причин результат каждого измерения отягощен погрешностью. Но, так как Хи и Хд неизвестны, погрешность ΔX также остается неизвестной. Она является случайной величиной и поэтому в лучшем случае может быть только оценена по правилам математической статистики. Это должно быть сделано обязательно, поскольку результат измерения без указания оценки его погрешности не имеет практической ценности.
3. Используя различные процедуры оценивания, находят интервальную оценку погрешности ΔX, в виде которой чаще всего выступают доверительные границы — 

4. Из предыдущего факта следует, что
истинное значение измеряемой величины находится с вероятностью Р в интервале [X— 

Таким образом, в результате измерения находят не истинное (или действительное) значение измеряемой величины, а оценку этого значения в виде границ интервала, в котором оно находится с заданной вероятностью.
Погрешности измерений могут быть классифицированы по различным признакам.
1. По способу выражения их делят на абсолютные и относительные погрешности измерений.
Таким образом, относительная погрешность измерения— отношение абсолютной погрешности измерения к истинному значению измеряемой величины или результату измерений.
Для характеристики точности СИ часто применяют понятие «приведенная погрешность», определяемое формулой
Таким образом, приведенная погрешность средства измерения — отношение абсолютной погрешности средства измерения в данной точке диапазона СИ к нормирующему значению этого диапазона.
2. По источнику возникновения погрешности измерений делят на инструментальные, методические и субъективные.
Инструментальная погрешность измерения — составляющая погрешности измерения, обусловленная несовершенством применяемого СИ: отличием реальной функции преобразования прибора от его калибровочной зависимости, неустранимыми шумами в измерительной цепи, запаздыванием измерительного сигнала при его прохождении в СИ, внутренним сопротивлением СИ и др. Инструментальная погрешность измерений разделяется на основную (погрешность измерений при применении СИ в нормальных условиях) и дополнительную (составляющая погрешности измерений, возникающая вследствие отклонения какой-либо из влияющих величин от ее номинального значения или ее выхода за пределы нормальной области значений). Метод их оценивания будет рассмотрен ниже.
Методическая погрешность измерений — составляющая погрещности измерений, обусловленная несовершенством метода измерений. К ней относят погрешности, обусловленные отличием принятой модели объекта измерения от реального объекта, несовершенством способа воплощения принципа измерений, неточностью формул, применяемых при нахождении результата измерений, и другими факторами, не связанными со свойствами СИ. Примерами методических погрешностей измерений являются:
• погрешности изготовления цилиндрического тела (отличие от идеального круга) при измерении его диаметра;
• несовершенство определения диаметра круглого тела как среднего из значений диаметра в двух его заранее выбранных перпендикулярных плоскостях;
• погрешность измерений вследствие кусочно-линейной аппроксимации нелинейной калибровочной зависимости СИ при вычислении результата измерений;
• погрешность статического косвенного метода измерений массы нефтепродукта в резервуаре вследствие неравномерности плотности нефтепродукта по высоте резервуара.
Субъективная (личная) погрешность измерения — составляющим погрешности измерения, обусловленная индивидуальными особенностями оператора, т. е. погрешность отсчета оператором показаний по шкалам СИ. Они вызываются состоянием оператора, несовершенством органов чувств, эргономическими свойствами СИ. Характеристики субъективной погрешности измерений определяют с учетом способности «среднего оператора» к интерполяции в пределах цены деления шкалы измерительного прибора. Наиболее известная и простая оценка этой погрешности — ее максимальное возможное значение в виде половины цены деления шкалы.
3. По характеру проявления разделяют систематические, случайные и грубые погрешности.
Грубой погрешностью измерений (промахом) называют погрешность измерения, существенно превышающую ожидаему при данных условиях погрешность. Они возникают, как правило из-за ошибок или неправильных действий оператора (неверный отсчет, ошибка в записях или вычислениях, неправильное включение СИ и др.). Возможной причиной промаха могут быть сбои работе технических средств, а также кратковременные резкие из менения условий измерений. Естественно, что грубые погрешности должны быть обнаружены и исключены из ряда измерений.
Более содержательно деление на систематические и случайные погрешности.
Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематические погрешности подлежат исключению насколько возможно, тем или иным способом. Наиболее известный из них — введение поправок на известные систематически погрешности. Однако полностью исключить систематическую погрешность практически невозможно, и какая-то ее небольшая часть остается и в исправленном (введением поправок) результате измерений. Эти остатки называются неисключенной систематической погрешностью (НСП). НСП — погрешность измерений, обусловленная погрешностями вычисления и введения поправок или же систематической погрешностью, на действие которой по правка не введена.
Например, с целью исключения систематической погрешности, измерения, обусловленной нестабильностью функции npeoбpaзования аналитического прибора, периодически проводят его калибровку по эталонным мерам (поверочным газовым смесям или стандартным образцам). Однако, несмотря на это, в момент измерения все равно будет некоторое отклонение действительной функции преобразования прибора от калибровочной зависимости, обусловленное погрешностью калибровки и дрейфом функции преобразования прибора за время, прошедшее после калибровки. Погрешность измерения, обусловленная этим отклонением, является НСП.
Случайной погрешностью измерения называется составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же шпчины. Причины случайных погрешностей многообразны: шумы измерительного прибора, вариация его показаний, случайные колебания параметров электрической сети и условий измерений, погрешности округления отсчетов и многие другие. В появлении таких погрешностей не наблюдается какой-либо закономерности, они проявляются при повторных измерениях одной и той же величины в виде разброса результатов измерений. Поэтому оценивание случайных погрешностей измерений возможно только на основе математической статистики (эта математическая дисциплина родилась как наука о методах обработки рядов измерений, отягощенных случайными погрешностями).
В отличие от систематических, случайные погрешности нельзя исключить из результатов измерений путем введения поправок, однако их влияние можно существенно уменьшить проведением многократных измерений.
Элементы теории погрешностей
Понятие погрешности
При любой степени совершенства и точности измерительной аппаратуры, рационально спланированной методике измерений, тщательности выполнения измерительных операций результат измерений отличается от истинного значения физической величины.
Иначе говоря, при всяком измерении неизбежны обусловленные разнообразными причинами отклонения результата измерения ( x ) от истинного значения измеряемой величины (X). Эти отклонения называют погрешностями измерений.
Это соотношение служит исходным для теоретического анализа погрешностей. На практике же из-за невозможности определить истинное значение вместо него берут действительное значение измеряемой величины, например, среднеарифметическое результатов наблюдений при измерениях с многократными наблюдениями.
Истинным называется значение ФВ (физической величины), идеальным образом характеризующее свойство данного объекта, как в количественном, так и качественном отношении. Оно не зависит от средств нашего познания и является той абсолютной истиной, к которой мы стремимся, пытаясь выразить её в виде числовых значений.
Действительным называется значение ФВ, найденное экспериментально и настолько близкое к истинному, что в поставленной измерительной задаче оно может быть использовано вместо него.
Погрешность измерений иногда удобно характеризовать ее относительным значением:
Следует также различать погрешность результата измерения и погрешность средства измерений ( СИ ). Эти два понятия во многом близки друг к другу и классифицируются по одинаковым признакам.
Величину, обратную относительной погрешности, называют точностью:
Правильное количественное представление о качестве измерений получают путем указания погрешности или точности. Соответствующие формулировки будут:
Точность 1000 соответствует относительной погрешности 0,1%, точность 25 – относительной погрешности 4%.
Классификация погрешностей
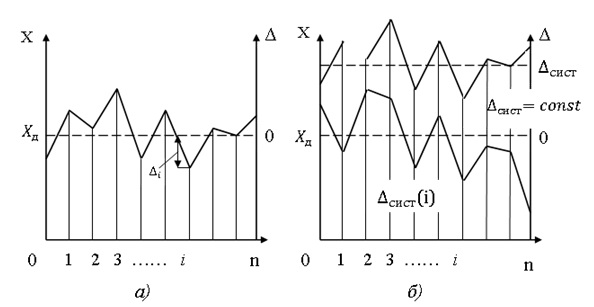
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом ( по знаку и значению) в серии повторных измерений одного и того же размера физической величины, проведенных с одинаковой тщательностью в одних и тех же условиях.
В появлении таких погрешностей, изображенных на рис. 2.1(а), не наблюдается какой-либо закономерности, они обнаруживаются при повторных измерениях одной и той же величины в виде некоторого разброса получаемых результатов. Случайные погрешности неизбежны, неустранимы и всегда присутствуют в результате измерения, однако их можно существенно уменьшить, увеличив число наблюдений.
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же физической величины. Постоянная и переменная систематические погрешности показаны на рис. 2.1(б). Их отличительный признак заключается в том, что они могут быть предсказаны, обнаружены и благодаря этому почти полностью устранены введением соответствующей поправки.
Прогрессирующая погрешность – это понятие, специфичное для нестационарного случайного процесса изменения погрешности во времени, оно не может быть сведено к понятиям случайной и систематической погрешностей.
По способу выражения разделяют абсолютные, относительные и приведенные погрешности.
Алгебраическую разность измеряемого значения величины x и действительного ее значения a называют абсолютной погрешностью измерения 
Отношение абсолютной погрешности к действительному значению измеряемой величины 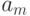
Отношение абсолютной погрешности к максимальному возможному значению измеряемой величины (например, к верхнему пределу измерений прибора или к диапазону измерений) называется приведенной погрешностью 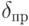
В зависимости от причин возникновения различают инструментальные погрешности измерения, погрешности метода измерений, погрешности из-за изменения условий измерения и субъективные погрешности измерения.
Погрешность метода измерений – составляющая систематической погрешности измерений из-за несовершенства принятого метода измерений, эта погрешность обусловлена:
Погрешность (измерения) из-за изменения условий измерения – это составляющая систематической погрешности измерения, являющаяся следствием неучтенного влияния отклонения в одну сторону какого-либо из параметров, характеризующих условия измерений, от установленного значения.
Этот термин применяют в случае неучтенного или недостаточно учтенного действия той или иной влияющей величины (температуры, атмосферного давления, влажности воздуха, напряженности магнитного поля, вибрации и др.); неправильной установки средств измерений, нарушения правил их взаимного расположения и др.
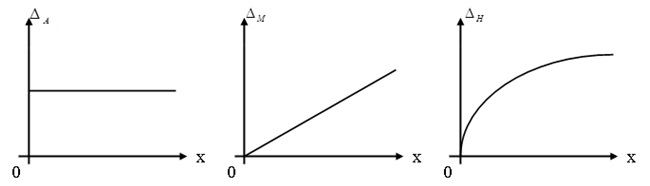
По зависимости абсолютной погрешности от значений измеряемой величины различают погрешности: аддитивные 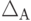
Классификация погрешностей.
| № | Признак | Виды погрешностей |
| Измерений | Средств измерений | |
| По способу выражения | Абсолютная Относительная | Абсолютная Относительная Приведенная |
| По источнику возникновения | Методическая Инструментальная Субъективная | Инструментальная |
| По характеру проявления | Систематическая Случайная Грубая (промах) | Систематическая Случайная |
| В зависимости от условий применения СИ | – | Основная Дополнительная |
| В зависимости от характера поведения измеряемой физической величины в процессе измерения | – | Статическая Динамическая |
| По характеру зависимости от измеряемой величины | – | Аддитивная Мультипликативная |
1. По способу выражения различают абсолютную, относительную и приведенную погрешность.
Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины и определяемая согласно выражения (1.2). Абсолютная погрешность сама по себе не может служить показателем точности измерений, так как одно и то же ее значение, например Δ = 0,05 мм, при X = 100 мм соответствует довольно высокой точности измерений, а при X = 1 мм – низкой.
Поэтому вводится понятие относительной погрешности.
Относительная погрешность – это погрешность, выраженная отношением абсолютной погрешности к действительному значению. Во многих случаях она является более наглядной характеристикой оценки качества результата измерения. Относительную погрешность δ находят из выражения
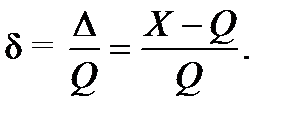
Относительную погрешность выражают в относительных единицах или в процентах (в последнем случае в формуле (1.3) к правой части добавляется множитель 100 %).
Приведенная погрешность – это относительная погрешность, в которой абсолютная погрешность средства измерений отнесена к условно принятому значению ХN, постоянному на всем диапазоне измерений или его части:
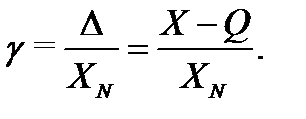
где XN – нормирующее значение. За нормирующее значение часто принимают верхний предел измерений. Указание погрешности измерений в виде относительной приведенной погрешности говорит о том, что абсолютная погрешность измерений Δ постоянна на всем диапазоне (поддиапазоне) измерений.
2. По причине возникновения различают методическую, инструментальную и субъективную погрешности.
Методическая погрешность (Δм) – это составляющая систематической погрешности измерения, возникающая из-за несовершенства принятого метода измерения. Эта погрешность, в основном, проявляется как систематическая погрешность, но иногда может проявляться как случайная методическая погрешность, например погрешность, обусловленная влиянием повторной установки объекта измерения на измерительную позицию, влиянием дискретности измеряемой ФВ и др.
Примеры: 1. Влияние радиационного нагрева при измерении температуры термометром, размещенным на солнце.
2. Влияние входного сопротивления вольтметра на результат измерения напряжения.
Инструментальная погрешность(Δинс) – это составляющая погрешности измерения, обусловленная погрешностью применяемого СИ. Например, инструментальная погрешность может быть обусловлена нелинейностью преобразования сигнала, ограниченностью динамического диапазона, инерционностью СИ, изменением условий эксплуатации (температуры окружающей среды, электромагнитными помехами, колебаниями напряжения в сети питания). Инструментальная погрешность складывается из основной и дополнительных погрешностей.
Субъективная погрешность(Δсуб) – это составляющая систематической погрешности измерения, обусловленная индивидуальными особенностями оператора. Например, при отсчитывании показаний СИ в аналоговом виде большое значение имеет правильное расположение оператора по отношению к показывающему устройству. Некоторые операторы систематически опаздывают с отсчетом показаний.
3. По характеру проявления различают систематическую, случайную и грубую погрешности.
Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности могут быть предсказаны, обнаружены и исключены (уменьшены) из результата измерений введением поправок. Например: погрешности от измерения температуры и др. влияющих факторов. Погрешности такого рода являются не изменяющимися во времени функциями вызывающих их влияющих величин (температуры, частоты, напряжения и пр.).
Поправки всегда определяются и вычисляются с некоторой погрешностью, часть систематических погрешностей так или иначе оказывается необнаруженной, поэтому существует понятие неисключенная систематическая погрешность (НСП). Иногда этот вид погрешности называют неисключенными остатками систематической погрешности, остающимися после введения поправок и содержащимися в результате измерений.
В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные, периодическиеипогрешности, изменяющиеся по сложному закону.
Постоянные погрешности – погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений. Они встречаются наиболее часто.
Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся, например, погрешности вследствие износа измерительных наконечников, контактирующих с деталью при контроле ее прибором активного контроля.
Периодические погрешности – погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
Случайная погрешность – составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений физической величины постоянного размера, проведенных с одинаковой тщательностью в одинаковых условиях. В появлении таких погрешностей не наблюдается какой-либо закономерности, они проявляются при повторных наблюдениях в виде некоторого разброса полученных результатов. Случайные погрешности неустранимы и всегда присутствуют в результате измерения. Описание предельных значений случайных погрешностей возможно на основе теории случайных процессов и математической статистики. Уменьшение случайных погрешностей возможно путем увеличения числа наблюдений.
Грубая погрешность (промах) – это погрешность, которая при исправных средствах измерений и корректных действиях экспериментатора (оператора) не должны появляться. Причина промахов – ошибки оператора, сбои в работе аппаратуры, скачки напряжения в сети, вибрация и т. п. Промахи проявляются они в том, что результаты отдельных измерений резко отличаются от остальных. При однократном измерении промах может быть обнаружен только путем логического анализа или сопоставления результата с априорным представлением о нем. Если причина промаха установлена, то результат однократного измерения следует признать ошибочным и повторить измерение. При многократном измерении одной и той же величины постоянного размера промахи проявляются в том, что результаты отдельных измерений, входящих в один ряд, резко отличаются от остальных результатов этого ряда. Такие промахи выявляют с помощью специальных критериев при обработке результатов измерений.
4. В зависимости от условий применения СИ различают основную и дополнительную погрешности.
Основная погрешность СИ – это погрешность СИ, применяемого в нормальных условиях.
Дополнительная погрешность СИ – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений. Примеры: дополнительные погрешности, вызванные изменением температуры окружающей среды, напряжения питания и др.
Дополнительные погрешности нормируют функциями влияния, которые могут иметь вид числа, формулы, таблицы или графика. В частности, дополнительная погрешность от изменения температуры окружающей среды может указываться в виде коэффициента, равного значению дополнительной погрешности, возникающей при изменении температуры на 1 или 10 °С, например: ±0,01 %/°С.
5. В зависимости от постоянства измеряемой величины различают статическую и динамическую погрешности.
Статическая погрешностьСИ – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.
Динамическая погрешность СИ – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины. Эта дополнительная динамическая составляющая погрешности обусловлена инерционными свойствами СИ, не способного отслеживать быстрое изменение измеряемой ФВ. Примерами динамических измерений являются измерения мгновенных значений быстро протекающих процессов.
Дата добавления: 2016-02-13 ; просмотров: 6153 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ