Сигма минус 1 это что
Как легко понять знаки Σ и П с помощью программирования
Для тех, кто подзабыл матешу
Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.
Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.
Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.
Знак Σ — сумма
Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:
Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.
На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:
Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».
Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:
Произведение П
С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:
А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:
Что дальше
Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.
Что такое «сигма»?
Сигмой (σ) в статистическом анализе обозначают стандартное отклонение. Опуская тонкости, которые будут обсуждены ниже, можно сказать, что стандартное отклонение — это та погрешность, то «± сколько-то», которым обязательно сопровождают измерение величины. Если вы измерили массу предмета и получили результат 100 ± 5 грамм, то величина «110 грамм» отличается от измеренного результата на два стандартных отклонения (то есть на 2 сигмы), величина «50 грамм» отличается на 10 стандартных отклонений (на 10 сигм).
Зачем всё это нужно: сигмы и вероятности
При обсуждении погрешностей мы уже говорили, что фраза «измеренная масса равна 100 ± 5 грамм» вовсе не означает, что истинная масса гарантированно лежит в интервале от 95 до 105 грамм. Она может оказаться и за пределами этого интервала «± 1σ», но, как правило, недалеко. В небольшом проценте случаев может даже случиться, что она выходит за пределы интервала «± 2σ», и уж совсем редко она оказывается за пределами «± 3σ». В общем, тенденция ясна: количество сигм связано с вероятностью того, что истинное значение будет настолько отличаться от измеренного.
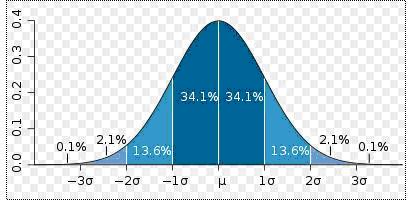
Вероятность того, что истинное значение попадет в определенный интервал около измеренного среднего значения при нормальном распределении ошибок. Изображение с сайта en.wikipedia.org
Пропустим все математические подробности и покажем результат для самого простого и распространенного случая, который называется «нормальное распределение» (см. рисунок). Вероятность попасть в интервал ± 1σ — примерно 68%, в интервал ± 2σ — примерно 95%, в интервал ± 3σ — примерно 99,8%, и т. д. Итак, можно сформулировать некую договоренность:
Договоренность: выражение какого-то отличия в количестве сигм — это сообщение о том, какова вероятность, что такое или еще более сильное отличие могло произойти за счет случайного стечения обстоятельств при измерении.
Использовать эту договоренность можно разными способами. Если вы просто сообщаете результат измерения (100 ± 5 грамм) и уверены в том, что нормальное распределение применимо, то вы можете сказать, что истинное значение массы с вероятностью 68% лежит в этом интервале, с вероятностью 95% лежит в интервале от 90 до 110 грамм, и т. д.
Эти выражения особенно стандартны, когда речь идет о поиске новой частицы. Вы сравниваете экспериментальные данные с теоретическим предсказанием, сделанным без новой частицы, и, если видите отличие от 3 до 5 сигм, вы говорите: получено указание на существование новой частицы (по-английски, evidence). Если же отличие превышает 5 сигм, вы говорите: мы открыли новую частицу (discovery).
Пример 1
Предположим, что вы изучаете какой-то редкий распад мезона и сравниваете его с теоретическим предсказанием в рамках Стандартной модели. Для удобства записи вы выразили результат измерения в виде такой величины:
μ = (измеренная вероятность распада) / (теоретически предсказанная вероятность распада)
и получили ответ: μ = 1,25 ± 0,25. Что вы можете сказать про этот результат?
Во-первых, он отличается от нуля на пять сигм. Значит, он уже классифицируется как открытие, и поэтому вы можете смело заявлять: мы открыли искомый распад мезона (если, конечно, это уже не сделал кто-то до вас; тогда вам придется довольствоваться скромным «подтверждением открытия»). Во-вторых, он отличается от единицы на одну сигму. Такое отклонение «неинтересно», оно не позволяет вам сказать, что вы обнаружили какое-то статистически значимое отличие от теоретических расчетов. Поэтому вы добавляете: измеренное значение согласуется с предсказаниями Стандартной модели.
Предположим далее, что вы набрали в 25 раз больше статистики, перемеряли эту вероятность и получили уточненное значение: μ = 1,20 ± 0,05. Отличие от нуля составляет уже 24 сигмы, так что сомнений в реальности эффекта больше не остается. Отличие от единицы составляет теперь 4 сигмы. Этого еще недостаточно для того, чтобы заявить, что вы открыли Новую физику. Но вы можете четко сказать, что ваши данные расходятся с теоретическими предсказаниями на уровне 4 сигм и указывают на существование эффекта вне Стандартной модели.
Пример 2
Вы изучаете рождение мюонов и антимюонов в каком-то процессе и хотите узнать, можно ли сделать вывод о том, что они рождаются с разной вероятностью. Для мюонов (μ – ) вы получили вероятность рождения x– = 0,18 ± 0,03, а для антимюонов (μ + ) – x+ = 0,30 ± 0,04. Разница получается 0,12, но насколько значимым является это различие?
Если для обеих погрешностей справедливы нормальные распределения, а также если эти погрешности полностью независимы (между ними нет корреляций), то общая погрешность величины x+ – x– вычисляется по формуле суммирования квадратов. Поэтому результат измерения x+ – x– = 0,12 ± 0,05. Отличие составляет 2,4 сигмы, и этого еще недостаточно для каких-либо серьезных выводов.
«Уверенность» против «статистической значимости»
Заметьте, что в приведенных выше примерах нас интересовали вопросы, на которые можно ответить «да» или «нет». Проступает ли в полученных данных какая-то новая частица? Согласуется ли распределение по импульсу с теоретическими расчетами? Зависит ли сечение процесса от энергии столкновений? Совпадает ли масса у частицы и ее античастицы? Попытка ответить на эти вопросы с помощью данных называется на научном языке проверкой гипотез. Вопросы, которые требуют развернутого ответа (подсчитать что-то, объяснить что-то и т. п.), гипотезами не называются.
В простейшем приближении результат экспериментальной проверки гипотезы выглядит так: ответ «да» с вероятностью p и ответ «нет» с вероятностью 1 – p. Эти вероятности очень важны для сообщения результата; физики обычно избегают абсолютных утверждений («мы открыли» или «мы опровергли») без указания вероятностей.
Но тут сразу же надо сделать важное уточнение. Если его четко осознать, то станет понятным, почему такие стандартные для научно-популярных новостей фразы, как «Ученые на 99% уверены, что открыли что-то новое», — обманчивы.
Точная формулировка, которую обычно используют ученые, такова:
При проверке гипотезы получен ответ «да» на уровне статистической значимости p.
При этом величина p часто выражается в виде количества сигм. В англоязычной литературе используется словосочетание confidence level, CL (доверительный уровень). В русскоязычной еще иногда говорят «статистическая достоверность», но такое выражение может привести к путанице в понимании.
Отличие «популярной» фразы от истинного утверждения вот в чём. Во всяком измерении есть не только статистические, но и систематические погрешности. Описанные выше правила связи вероятностей и количества сигм работают только для статистических погрешностей — и то если к ним применимо нормальное распределение. Если статистические погрешности всегда можно обсчитать аккуратно, то систематические погрешности — это немножко искусство. Более того, из многолетнего опыта известно, что сильные систематические отклонения уж точно не описываются нормальным распределением, и потому для них эти правила пересчета не справедливы. Так что даже если экспериментаторы всё перепроверили много раз и указали систематическую погрешность, всегда остается риск, что они что-то упустили из виду. Корректно оценить этот риск невозможно, поэтому вы на самом деле не знаете, с какой истинной вероятностью ваш ответ верен.
Конечно, по умолчанию систематическим погрешностям стоит доверять, особенно если они исходят от опытных экспериментальных групп. Но вековой опыт изучения элементарных частиц показывает, что несмотря на все предосторожности регулярно случаются проколы. Бывает, что коллаборация получает результат, сильно противоречащий какой-то гипотезе, перепроверяет анализ много раз и никаких ошибок у себя не находит. Однако этот результат затем не подтверждается другими — порой намного более точными! — экспериментами. Почему первый эксперимент дал такой странный результат, что в нём было не то, где там ошибка или неучтенная погрешность — всё это зачастую так и остается непонятым (впрочем, иногда источник ошибки быстро вскрывается, как это случилось со «сверхсветовыми» нейтрино в эксперименте OPERA).
Физики к таким оборотам событий уже привыкли, поэтому каждый экспериментальный результат, сильно отличающийся от всей сложившейся к тому времени картины, вызывает оправданный скепсис. Физики так консервативны в своем отношении вовсе не потому, что они ретрограды и намертво уверовали в какую-то одну теорию, как это хотят представить опровергатели физики. Они просто научены всем предыдущим опытом в физике частиц и знают, чем это обычно кончается. Поэтому без независимого подтверждения другими экспериментами подобные сенсации они не поддерживают.
ФЭЧ в сравнении с другими науками
Надо сказать, что сформулированные выше жесткие критерии статистической достоверности характерны именно для физики элементарных частиц и некоторых смежных разделов. Во многих других разделах физики, а тем более в других дисциплинах (в особенности, в биомедицинских науках) критерии намного слабее.
Предположим, вы измерили некие данные и хотите узнать, какова вероятность того, что они «вписываются в норму». Вы проводите статистический тест, который дает вам вероятность того, что «нормальная ситуация» без какого-либо реального отклонения только за счет статистической флуктуации даст вот такое или еще более сильное отклонение. Эта вероятность называется p-значение. В биологии пороговое p-значение, ниже которого уже уверенно говорят про реальное отличие, составляет один или даже несколько процентов. В физике элементарных частиц такое отличие вообще не считают значимым, тут нет даже «указания на существование» какого-то отличия! Ответственное заявление об отличии звучит в ФЭЧ только для p-значений меньше одной двухмиллионной (то есть отклонение больше 5σ). Такой жесткий подход к достоверности утверждений выработался в ФЭЧ примерно полвека назад, в эпоху, когда экспериментаторы видели много отклонений со значимостью в районе 3σ и смело заявляли об открытии новых частиц, хотя потом эти «открытия» не подтверждались. Подробный рассказ об истоках этого критерия см. в постах Tommaso Dorigo (часть 1, часть 2).
Суть стат. контроля



В предыдущих параграфах я уже говорил о разбросе значений (вариации) в группе значений. Любую группу данных можно охарактеризовать средним значением (сумма всех значений, поделенная на количество значений) и среднеквадратическим отклонением (стандартное отклонение, показатель, который характеризует рассеивание значений в группе, степень близости значений к среднему группы).
1 Большое стандартное отклонение, большой разброс между максимальными значениями, минимальными и средним в группе.
2 Маленькое стандартное отклонение, небольшой разброс между максимальными значениями, минимальными и средним в группе.
Среднеквадратичное отклонение (далее сигма) имеет большое прикладное применение в разных процедурах контроля качества. В случае стат. контроля одно свойство является бесценным:
В стабильном процессе с нормальным распределением значения располагаются на определенном удалении от среднего.
На диаграмме мы видим, что
— 68,2 % из всех значений находятся на удалении плюс минус 1 сигма от среднего
— 95,5 % из всех значений находятся на удалении плюс минус 2 сигмы от среднего
— 99,7 % из всех значений находятся на удалении плюс минус 3 сигмы от среднего.
Так что любое значение из группы данных стабильного процесса имеет определенную вероятность находиться на определенном расстоянии от среднего.
Вероятность того, что каждая новая нарабатываемая деталь в стабильном процессе будет иметь длину в пределах одной сигма от среднего значения – 68,2 %.
Вероятность того, что каждая новая нарабатываемая деталь в стабильном процессе будет иметь длину в пределах двух сигм от среднего значения – 95,5 %.
Вероятность того, что каждая новая нарабатываемая деталь в стабильном процессе будет иметь длину в пределах трех сигм от среднего значения – 99,7 %.
Обратите внимание на тот факт, что нижняя и верхняя границы графика это не нормы приемки сдачи!
Это естественные границы стабильного процесса! Плюс минус 3 сигма.
Виды графиков стат. контроля:
В зависимости от целей применения используют разные виды графиков.
Две основные группы графиков – графики для переменных (количественные признаки) и атрибутов (качественные признаки).
| Вид данных | Название графика | Обозначаемые данные |
| Переменные | График средних и размахов | Средние значения выборки и значения размаха |
| График средних и стандартных отклонений | Средние значения выборки и стандартные отклонения выборки | |
| График значений и двигающихся размахов | Индивидуальные значения и двигающиеся размахи | |
| График медиан и размахов | Медианы и размахи выборки | |
| Атрибуты | График p | Пропорция дефектных деталей в выборке |
| График np | Количество дефектных деталей в выборке | |
| График с | Количество дефектов на одну деталь в выборке | |
| График u | Средний номер дефектов на единицу продукции |
В большинстве случаев мы не можем измерять каждую деталь. Стат. контроль использует выборку (часть деталей) из популяции (все проверяемые данные).
Как пример – каждые 2 часа проверяется 5 деталей из производимых на линии.
На основании данных вычисляется
— точка для графика средних
— точка для графика размахов
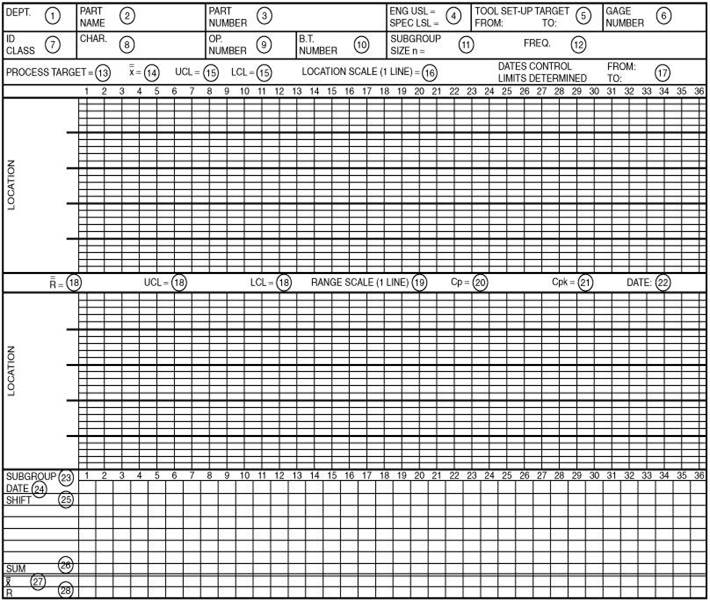
Пример формы для графика средних и размахов
Формула для расчета графиков средних и размахов
Интерпретация графиков стат. контроля:
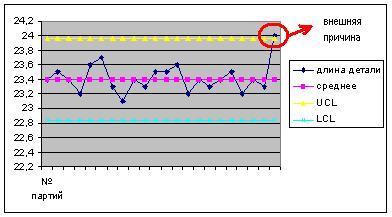
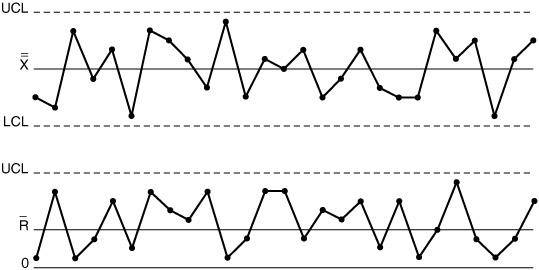
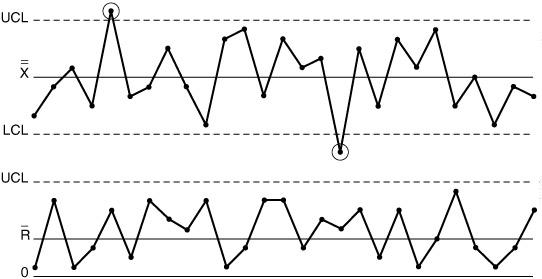
Все графики, кроме первого, показывают случаи систематической вариации.
1 Стабильный и предсказуемый процесс
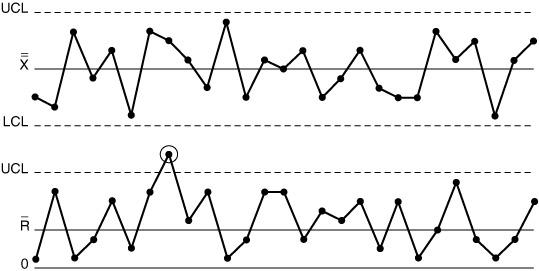
2 Процесс с точкой выше верхнего контрольного предела на графике размахов
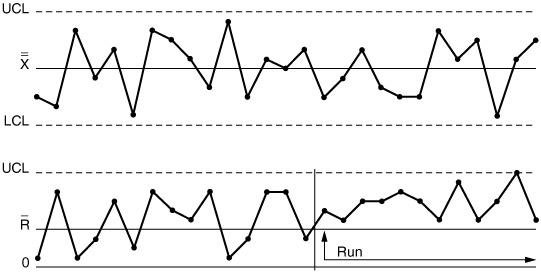
3 Процесс с «пробегом» точек над средними значениями в графике размахов
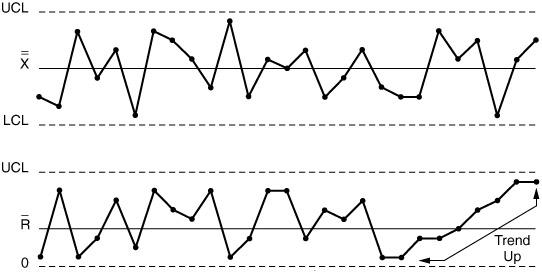
4 График с тенденцией (трендом) на графике размахов
5 Процесс с точками вне контрольных пределов на графике средних
6 Процесс с тенденцией вниз на графике средних
Сигма минус 1 это что
Сигма-минус-гиперон (физики шутят)
Впервые это я прочел в стенгазете «Физик» физфака РГУ в 1966 году, будучи первокурсником. Запомнил на всю жизнь, правда, не все. Через много лет это рассказал наш замечательный А.Г.Филиппенко, тоже физик по образованию. По стилю стиха он принаждежит, скорее всего, Б.Г.Режабеку, биофизику из РГУ, личности легендарной, блестящего остроумия. Что стих ростовский, говорит и «трамвай десятый номер» в конце стиха. Этот трамвай ходил мимо здания физфака по тихой тогда улице М.Горького, дом 88. На красной кирпичной стене дома не исчезала и регулярно подновлялась крупная надпись мелом: «Ура, 3. «. Подозреваю, что физтеховцы тихо слямзили этот стих в Ростове, после чего он появился в физтехе и стал известен А.Г.Филиппенко, который наверняка не смог не обратить на него внимание.
Стих привожу и по памяти, и по публикациям в сети, в которых я изменил только то, что точно помню. Если кто-то что-то точно знает, поправьте. Что-то там еще не так, выпадает из стиля.
У меня прогорел циклотрон.
Что за шум поднялся, что за звон!
Я влезаю в ускоритель,
Выпрямляю выпрямитель.
Что за чудо, что за чёрт?!
Квант идёт не первый сорт.
Это он, это он,
Сигма-минус-гиперон!
Гиперон, гиперон, гиперонище!
«Ты сегодня не в лице,
Говорит.
Ты пойди-ка на ВЦ,
Говорит.
Всё в масштабе рассчитай,
Говорит.
А потом и приезжай,
Говорит.»
И вскочил я на фигуру Лиссажу
И одно только слово твержу:
«Гиперон, гиперон, гиперонище!»
Я не спал четыре ночи,
Не смыкал все ночи очи.
Я не спал четыре дня,
Утомленье у меня.
От такого утомленья
Начинаются виденья.
Полюса те не простые,
Всем обычным не чета,
Вычета в них нулевые,
Нулевые вычета.
Синус больше единицы.
Нуль не нуль, а два нуля.
Метод Ритца не годится,
Виртуально говоря.
И закон Гейзенберга не действует.
И прочёл я в научном журнальчике,
Хоть и верно я взял интервальчики,
Но не вычислить мне интегральчиков
Без лагранжевых функциональчиков.
А считать их надо стохастически.
Всё то сразу я прочёл.
Как мне стало хорошо.
И какое веселье тут началось.
Все частицы космические
Танцы пляшут фантастические.
Даже старые корпускулы
Разминают свои мускулы.
Аж от радости спины повыгнули.
«Вот теперь тебя люблю я,
Уважаю, молодца»
Шёл трамвай десятый номер
Ламца-дрица, гоп, ца-ца!
Пределы трех сигм
Что такое Пределы трех сигм?
Ключевые моменты:
Понимание пределов трех сигм
Контрольные диаграммы также известны как диаграммы Шухарта, названные в честь Уолтера А. Шухарта, американского физика, инженера и статистика (1891–1967).1 Контрольные диаграммы основаны на теории, согласно которой даже в идеально спроектированных процессах существует определенная вариативность выходные измерения присущи.
Контрольные диаграммы определяют, есть ли в процессе контролируемое или неконтролируемое изменение. Считается, что отклонения в качестве процесса по случайным причинам находятся под контролем; Неконтролируемые процессы включают как случайные, так и особые причины отклонений. Контрольные карты предназначены для определения наличия особых причин.
Для измерения вариаций статистики и аналитики используют показатель, известный как стандартное отклонение, также называемый сигмой. Сигма – это статистическое измерение изменчивости, показывающее, насколько существует отклонение от среднего статистического значения.
Краткая справка
Сигма измеряет, насколько наблюдаемые данные отклоняются от среднего или среднего значения; инвесторы используют стандартное отклонение для измерения ожидаемой волатильности, известной как историческая волатильность.
Пример расчета предела трех сигм
Давайте рассмотрим производственную фирму, которая проводит серию из 10 тестов, чтобы определить, есть ли различия в качестве ее продукции. Точки данных для 10 тестов: 8,4, 8,5, 9,1, 9,3, 9,4, 9,5, 9,7, 9,7, 9,9 и 9,9.
Особые соображения
Термин «три сигмы» указывает на три стандартных отклонения. Шухарт установил три предела стандартного отклонения (3-сигма) в качестве рационального и экономичного ориентира для минимальных экономических потерь. Пределы трех сигм устанавливают диапазон для параметра процесса в 0,27% контрольных пределов. Пределы контроля трех сигм используются для проверки данных процесса и их соответствия статистическому контролю. Это делается путем проверки того, находятся ли точки данных в пределах трех стандартных отклонений от среднего. Верхний контрольный предел (UCL) установлен на уровне трех сигм выше среднего, а нижний контрольный предел (LCL) установлен на трех уровнях сигма ниже среднего.
Поскольку около 99,99% управляемого процесса будет происходить в пределах плюс-минус трех сигм, данные процесса должны приблизительно соответствовать общему распределению вокруг среднего значения и в заранее определенных пределах. На кривой колокола данные, которые лежат выше среднего и за линией трех сигм, представляют менее 1% всех точек данных.