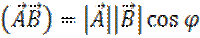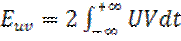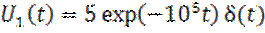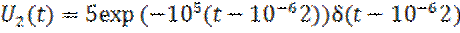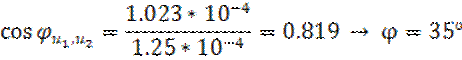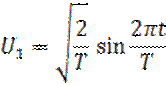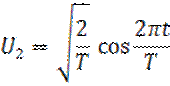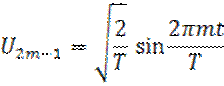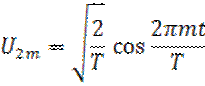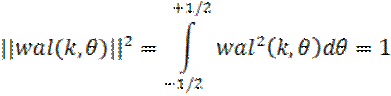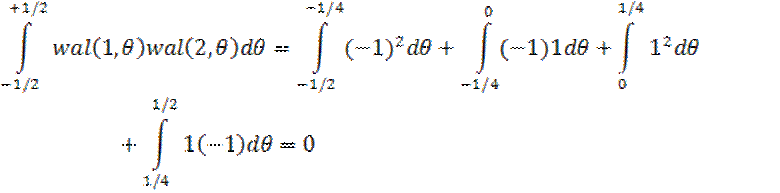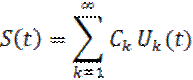Что такое ортогональный сигнал
Что такое ортогональный сигнал
Введя в множестве сигналов структуру линейного пространства, определив норму и метрику, мы, тем не менее, лишены возможности вычислить такую характеристику, как угол между двумя векторами.
Это, удается сделать, сформулировав важное понятие скалярного произведения элементов линейного пространства.
Скалярное произведение сигналов.
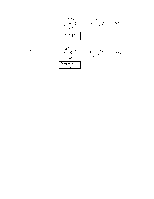
Напомним, что если в обычном трехмерном пространстве известны два вектора А и 
где 

Действуя по аналогии, вычислим энергию суммы двух сигналов
Сравнивая между собой формулы (1.18) и (1.19), определим скалярное произведение вещественных сигналов 
а также косинус угла между ними:
Скалярное произведение обладает свойствами:
1.
2.
3. 

4.
Линейное пространство с таким скалярным произведением, полное в том смысле, что оно содержит в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства, называется вещественным гильбертовым пространством Н.
Справедливо фундаментальное неравенство Кошн — Буняковского
Если сигналы принимают комплексные значения, то можно определить комплексное гильбертово пространство, введя в нем скалярное произведение по формуле
такое, что 
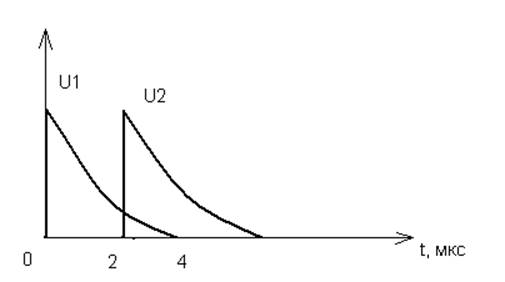
Пример 1.11. Имеются два смещенных во времени экспоненциальных импульса (В):
Найти скалярное произведение данных сигналов, а также угол 
Энергии этих сигналов одинаковы:
Отсюда 
Ортогональные сигналы и обобщенные ряды Фурье.
Два сигнала 
Пусть Н — гильбертово пространство сигналов с конечным значением энергии. Эти сигналы определены на отрезке времени 

Говорят, что при этом в пространстве сигналов задан ортонормированный базис.
Разложим произвольный сигнал 
Представление (1.27) называется обобщенным рядом Фурье сигнала 
Коэффициенты данного ряда находят следующим образом: Возьмем базисную функцию 
Ввиду ортонормированности базиса в правой части равенства (1.28) останется только член суммы с номером 
Возможность представления сигналов посредством обобщенных рядов Фурье является фактом большого принципиального значения. Вместо того чтобы изучать функциональную зависимость в несчетном множестве точек, мы получаем возможность характеризовать эти сигналы счетной (но, вообще говоря, бесконечной) системой коэффициентов обобщенного ряда Фурье с.
Примеры ортонормированных базисов.
Способы построения систем взаимно ортогональных функций подробно изучены в математике (см., например, [7]). Здесь в качестве примеров будут описаны две наиболее важные и распространенные системы.
Ортонормированная система гармонических функций. Читатель может самостоятельно убедиться в том, что на отрезке 
образует ортонормированный базис.
Разложение периодических функций в ряды Фурье по этой системе будет подробно рассмотрено в гл. 2.
Ортонормированная система функций Уолшр. В последнее время под влиянием методов обработки дискретных сигналов большое внимание уделяют ортонормированной системе функций Уолша, которые на отрезке своего существования 
Введем безразмерное время 


Очевидна нормированность функций Уолша при любом значении k:
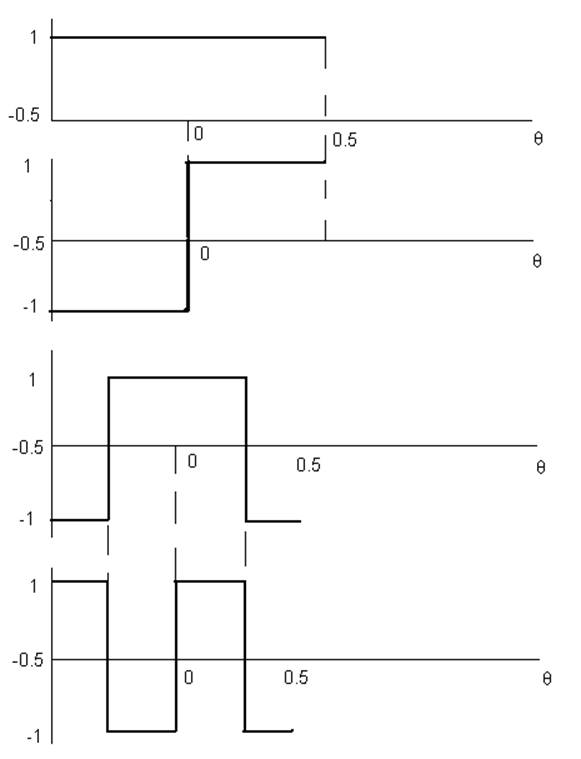
Рис. 1.4. Графики нескольких первых функций Уолша
Ортогональность этих функций следует из принципа их построения и может быть проверена непосредственно. Например:
Разложение сигнала с. конечной энергией, заданного на отрезке времени 

Пример 1.12. Найти перше два коэффициента в разложении гимпульса треугольной формы по системе функций Уолша.
На отрезке времени 
Вычисляем коэффициенты обобщенного ряда Фурье:
Итак, при аппроксимации колебания треугольной формы двумя первыми членами ряда по системе функций Уолша получается приближенное представление ступенчатой формы. Отметим, что с точки зрения введенной выше энергетической нормы уже такая грубая аппроксимация является удовлетворительной. Действительно, энергия исходного сигнала
в то время как энергия разности
составляет лишь 
Энергия сигнала, представленного в форме обобщенного ряда Фурье.
Рассмотрим некоторый сигнал 
и вычислим его энергию, непосредственно подставив, этот ряд в соответствующий интеграл:
Поскольку базисная система функций ортонормнрована, в сумме (1.32) отличными от нуля окажутся только члены с номерами 
Смысл этой формулы таков: энергия сигнала есть сумма энергий всех компонент, из которых складывается обобщенный ряд Фурье.
Оптимальность разложения сигнала по ортогональному базису. Для сигналах 
с не известными пока коэффициентами с и выберем эти коэффициенты так, чтобы минимизировать энергию ошибки аппроксимации:
Необходимое условие минимума состоит в том, что коэффициенты должны удовлетворять системе линейных уравнений
В развернутой форме энергия ошибки аппроксимации
Поскольку рассматриваемая базисная система функций ортогональна, отсюда следует, что
Приняв во внимание единичную норму базисных функций, приходим к выводу, что равенства (1.35) будут выполняться, если
что полностью совпадает с выражением (1.29) для коэффициентов обобщенного ряда Фурье,
Более тщательный анализ (на нем здесь не останавливаемся), когда рассматривается также вторая производная энергии ошибки, показывает, что при разложении сигнала в обобщенный ряд Фурье обеспечивается не просто экстремум, а именно минимум энергии ошибки аппроксимации.
Напомним в заключение, что гильбертово пространство сигналов, по определению, обладает важным свойством полноты: если предельное значение суммы
существует, то этот предел сам является некоторым элементом гильбертова пространства.
В полном функциональном пространстве норма ошибки аппроксимации монотонно убывает с ростом N — числом учитываемых членов ряда. Выбирая N достаточно большим, всегда можно снизить норму ошибки до любой приемлемо малой величины.
Аппаратурная реализация ортогонального разложения сигнала.
Рассмотрим структурную схему устройства для экспериментального определения коэффициентов разложения аналогового сигнала в обобщенный ряд Фурье по заданной системе ортонормированных базисных функций (рис. 1.5).
Основными элементами здесь являются генераторы тех базисных функций, по которым проводится разложение. Анализируемый сигнал одновременно подается на совокупность множительных звеньев, осуществляющих перемножение этого сигнала и соответствующей базисной функции. С. выходов перемножителей сигналы поступают на интеграторы. При таком методе обработки сигнала в конце промежутка времени интегрирования на выходе каждого интегратора возникает неизменный во времени уровень, величина которого в соответствии с формулой (1.29) в точности равна тому или иному коэффициенту обобщенного ряда Фурье.
Рис. 1.5. Структурная схема устройства для аппаратурного анализа сигналов
Ясно, что работоспособность системы в целом будет зависеть от того, насколько точно удается воссоздать базисные функции, а также от совершенства функционирования перемножителей и интеграторов.
Система, изображенная на рис. 1.5, важна и в прикладном, и в теоретическом смысле. Анализируя ее, еще раз убеждаемся, что вся информация, заключенная в сигнале, может быть представлена в виде хотя и бесконечной, но все же счетной совокупности чисел.
НЕКОГЕРЕНТНЫЕ приемники в радиосвязи
Для некоторых видов модуляции, например для амплитудной, частотной не обязательно знать начальную фазу сигнала, т.к. информация заключена в других параметрах, в амплитуде и частоте. Потому что там заложена информация либо в частоте либо в амплитуде, а не в начальной фазе сигнала. Соответственно можно сделать приемник таким образом, чтобы там не было системы синхронизации с несущей и при этом, чтобы приемник не был чувствителен к начальной фазе сигнала, т.е. чтобы он был некогерентным.
Если начальная фаза принимаемого сигнала и фаза опорного сигнала приемника не будут синхронизированы?
Ортогональность сигналов
Ортогональными сигналами называют сигналы у которых коэффициент корреляции равен нулю.
Корреляция это произведение двух сигналов и интеграл от этого произведения. Корреляция это некая степень похожести, чем больше коэффициент корреляции, тем два сигнала больше похожи друг на друга. Если коэффициент корреляции равен единице, то сигналы совпадают, а если нулю, то эти сигналы максимально не похожи друг на друга.
Сигналы s1(t) и s2(t) длительностью Тs называются ортогональными, если их коэффициент корреляции равен нулю:
Оптимальный некогерентный приемник АМн сигналов
A=√I^2+Q^2
Если теперь внимательно посмотреть на правую часть приемника, можно увидеть, что в структуре реализовано данное выражение: A=√I^2+Q^2, вычисление амплитуды по квадратурам. В данном приемнике вне зависимости от начальной фазы принимаемого сигнала будет корректно определена амплитуда сигнала.
Некогерентный приемник 2-ЧМн
На рисунке ниже представлена структура оптимального некогерентного приемника сигналов с двоичной частотной манипуляцией. В данном случае количество корреляторов составляет 4, при том, что количество сигналов в ансамбле два. Для каждого сигнала по два коррелятора. Верхние два корреляторы работают на одну частоту, выделяют из шумов сигнал с частотой ω1, нижние два коррелятора выделяют сигнал с частотой ω2.
Вероятность битовой ошибки
Рассмотрим, от чего зависит вероятность битовой ошибки, если принимать сигналы с разными видами модуляции оптимальными приёмниками. Аналитическое выражение для получения вероятности битовой ошибки для двоичных равновероятных сигналов, сюда можем отнести АМн,ЧМн и ФМн:
Из выражения, представленного выше, видно, что вероятность битовой ошибки Pb определяется тремя параметрами: Eb, Rb и No.
Чем больше энергия бита, тем меньше вероятность битовой ошибки. Под энергией бита подразумевается энергия сигнала, передающего один бит информации. В свою очередь Eb пропорциональна средней мощности сигнала и длительности бита.
Коэффициент взаимной корреляции Rb – это численный показатель схожести двух сигналов. Чем сигналы сильнее отличаются друг от друга, тем сложнее перепутать их друг с другом. Ошибка возникает из-за того, что путают один сигнал с другим из-за воздействия шумов.
Такой модуляцией может являться 2-ЧМн. В общем случае, коэффициент взаимной корреляции зависит от разницы частот двух сигналов s1(t) и s2(t), но при некоторой разнице частот, 2-ЧМн становится ортогональной модуляцией.
Из данного выражения видно, что энергия сигнала удвоилась, по сравнению с ортогональной модуляцией. Из этого можно сделать вывод о том, что 2-ФМн является более помехоустойчивой (в 2 раза по энергетике), чем ортогональная 2-ЧМн.
где f1 и f2 – частоты сигналов s1(t) и s2(t) соответственно.
Если по выражению Rb построить график, то можно увидеть, что коэффициент корреляции уменьшается с ростом разницы частоты.
Однако также можно наблюдать, что когда разница частот удовлетворяет условию: f2-f1=n/2T то коэффициент взаимной корреляции становится равен нулю.
На рисунке ниже представлен график зависимости вероятности битовой ошибки Pb при когерентном приеме ортогональной 2ЧМн (синий график) и 2ФМн (красный график).
Ортогональные сигналы. Скалярное произведение сигналов. Ортогональные сигналы и обобщенные ряды Фурье
Страницы работы
Содержание работы
1. Скалярное произведение сигналов.
2. Ортогональные сигналы и обобщенные ряды Фурье.
3. Примеры ортонормированных базисов.
4. Энергия сигнала, представленная в виде обобщенного ряда Фурье.
5.Апаратурная реализация разложения сигнала по ортонормированному базису.
Рассмотрев структуру ЛПС, определив норму и метрику, мы пока лишены возможности вычислить угол между векторами, это удается при введении скалярного произведения сигналов.
1. Если в обычном декартовом пространстве известны два вектора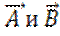
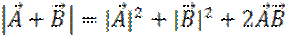
По аналогии вычислим энергию суммы двух сигналов U и V:
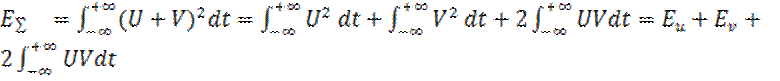
Сигналы U и V аддитивны, а их энергии нет. Энергия суммарного сигнала содержит в себе некую взаимную энергию:
Сравнивая (2) и (1) определяем скалярное произведение сигналов U и V:
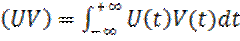
а также 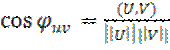
Свойства скалярного произведения сигналов (5):
3) (λU,V)=λ(U,V), λ – вещественное число.
ЛПС в котором введено скалярное произведение (3), при этом условия (5) – справедливы, то оно называется вещественным гильбертовым пространством H.
В гильбертовом пространстве справедливо неравенство Коши-Буняковского:
Для комплексного гильбертового пространства скалярное произведение:
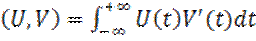
Пример: имеем 2 смещенных во времени экспоненциальных импульса напряжения:
Найти скалярное произведение сигналов 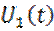
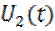
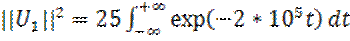
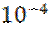
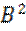
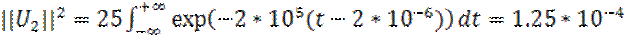
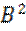
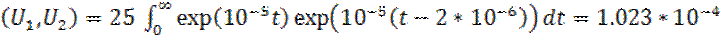
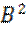
2. Два сигнала U, V – ортогональны, если их скалярное произведение и взаимная энергия равны нулю.
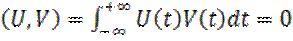
То есть ортогональные сигналы предельно не похожи друг на друга.
Пусть H – это гильбертовое пространство сигналов (ГПС) с конечным значением энергии. Эти сигналы определены на промежутке [t1, t2], конечном или бесконечном. Пусть на этом же интервале определена бесконечная система функций
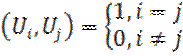
Следовательно, говорят, что при этом в ГПС задан ортонормированный базис.
Произвольный сигнал S(t), пренадлежащий H, можно разложить в следующий ряд:
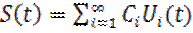
Получили обобщенный ряд Фурье.
Отыщем коэффициент ряда (10): C1, C2, …:
возьмем базисную функцию φk. Умножим на нее обе части (10) и проинтегрируем обе части по заданному интервалу [t1, t2].
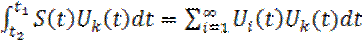
В следствии ортонормированности базиса правая часть (11) равняется Ck.
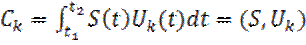
Из формулы (12) следует алгоритм вычисления коэффициентов C1, C2, … обобщенного ряда Фурье (ОРФ).
Представления сигналов ОРФ освобождает нас от необходимости изучать функциональную зависимость в несчетном множестве точек и дает право характеризовать эти сигналы коэффициентами C1, C2, …, которые являются проекциями вектора S(t) на базисные направления ГПС.
3. а) ортонормированная система гармонических сигналов на интервале [0,T] (13):
Разложение периодической функции в ряды Фурье по этой ортонормированной системе будет рассмотрено далее.
б) система функций Уолта.
Эта система, графики которой на рисунке 1, являются ортонормированными:
θ=t/T – безразмерное время. k–я функция – функция Уолта, обозначается wal(k, θ).
Интересно, что номер функции k равен числу перемен знака на интервале ее существования.
Проверим условие единичной нормы функции Уолта:
Проверим условие ортогональности функции Уолта:
Сигнал с конечной энергией, заданный на интервале (-Т/2; Т/2), можетбыть разложен в обобщенный ряд Фурье по функции Уолта так:
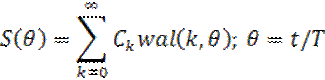
4. Пусть сигнал s(t) разложен в обобщенный ряд Фурье:
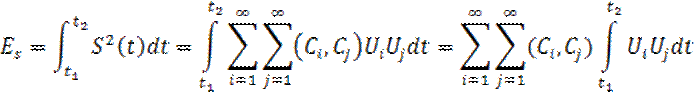
Поскольку базисная система ортонормированная, то в формуле (15) отличаются от нуля члены с i=j.
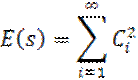
Следовательно, энергия сигнала равна сумме энергий всех компонент из которых складывается обобщенный ряд Фурье.
5. Схема, изображенная на рисунке, реализует алгоритм вычисления коэффициентов обобщенного ряда Фурье по формуле (12).
Ck появляется на выходе интеграторов в виде неизменного во времени сигнала в концне промежутка времени интегрирования.