Как поделить окружность на равные части
Деление окружности, или Геометрия для чайников
Приветствую всех мастеров и мастериц!
Очень многие из нас, учась в школе, думали, что очень многие предметы школьной программы в жизни нам никогда не понадобятся. Я так думала про геометрию. Однако жизнь сложилась так, что именно геометрия мне оказалась и нужна.
Одной из основных сложностей при создании круглого орнаменты является его симметричность. Иногда хочется, чтобу у нас был точный 8-ми гранник, иногда 5-ти конечная звезда, а иногда нужен 7-ми конечный цветок.
Эту глобальную проблему симметричного деления окружности на равное количество частей можно решить просто при помощи циркуля, линейки, листа бумаги и геометрии.
Деление окружности на 3 равных сектора.
Для начала нам понадобиться сама окружность. Рисуем ее при помощи циркуля
Ставим наш циркуль с набранным радиусом в точку, которую мы на окружности отметили и проводим дугу до пересечения с нашей основной окружностью.
Через точку на окружности и центр окружность проводим линию до пересечения с гранью.
Таким образом мы получили 3 точки на нашей окружности.
Теперь из центра проводим линии, соединяя центр с этими точками и у нас образовались 3 одинаковых сектора.
Деление окружности на 4 равных сектора.
Начинаем опять с окружности, необходимого нам диаметра. Назову ее окружность 1.
Через центр окружности 1 проводим линию до пересечения с обеими сторонами окружности 1.
Ставим ножку циркуля в точку на пересечении наше прямой линии и окружности 2 и из нее проводим дугу. Расстояние от точки на окружности до дуги равно диаметру окружности 1. (диаметр = 2 радиусам). Ту же процедуру повторяем с точкой на другой стороны окружности.
У нас есть 2 новые точки, появившиеся на пересечении дуг. Соединяем их и получаем окружность, разбитую на 4 ровных сектора.
Деление окружности на 5 равных секторов.
Начало работы с делением окружности на 5 частей очень схожа с делением окружности на 4 части, поэтому я начну уже с разделенного круга на 4 части.
Циркулем набираем радиус нашей окружности и ставим ножку в одну из имеющихся у нас точек. В моем случае это левая точка. Проводим дугу до пересечения ее с основной линии окружности.
Соединяем получившиеся точки при помощи линейки и находим новую точку пересечения (точка Н)
Циркулем набираем расстояние от верхний точки на окружности до точки Н. Ставим ножку в точку Н и проводим дугу и получаем еще одну точку (точка М)
Ставим ножку циркуля в верхнюю точку окружности и набираем расстояние до точки М.
Ставим ножку циркуля в верхнюю точку и откладываем набранное нами расстояние на нашей окружности.
Ставим циркуль в получившуюся точку и еще раз откладываем это расстояние. Таким же образом ставим еще 2 точки.
У нас получилось 4 отложенных точки и 1 верхняя точка окружности. Соединяем центр окружности с этими точками и получаем 5 равных секторов.
Деление окружности на 6 равных секторов.
Нам снова нужна окружность.
Берем любую точку на этой окружности, ставим в нее ножку циркуля с набранным расстоянием радиуса и проводим дугу до пересечения с нашей окружностью.
Далее соединяем выбранную нами точку с центром окружности и находим еще одну точку с противоположной стороны.
Из этой точки таким же расстоянием проводим еще одну дугу.
Деление окружности на 7 равных секторов.
Чтобы не повторяться и не описывать уже знакомые алгоритмы, берем за основу момент нахождения точки Н для разбития окружности на 5 частей.
Отмеряем циркулем расстояние от точки Н до точки на окружности.
Ставим ножку циркуля в верхнюю точку и набранным на циркуле расстоянием откладываем точки, аналогично как мы делали в случае разбивки окружности на 5 частей
Соединяем наши новые точки с центром и получаем 7 равных секторов.
Используя эти простые приемы можно создавать геометрические орнаменты различной сложности
Деление окружности на любое число равных частей
Как разделить окружность на заданное количество одинаковых частей, терминология при построении окружности, деление окружности на 3, 4, 5, 6, 8, 10 частей.
Термины при построениях окружности
Окружностью называется замкнутая кривая линия, каждая точка которой расположена на одинаковом расстоянии от одной точки О, называемой центром.
Прямые линии, соединяющие любую точку окружности с её центром, называют радиусами R.
Прямая АВ, соединяющая две точки окружности и проходящая через её центр О, называется диаметром D.
Части окружностей называются дугами.
Прямая СD, соединяющая две точки на окружности, называется хордой.
Прямая МN,которая имеет только одну общую точку с окружностью называется касательной.
Часть круга, ограниченная хордой СD и дугой, называется сигментом.
Часть круга, ограниченная двумя радиусами и дугой, называется сектором.
Две взаимно перпендикулярные горизонтальная и вертикальная линии, пересекающиеся в центре окружности, называются осями окружности.
Угол, образованный двумя радиусами КОА, называется центральным углом.
Два взаимно перпендикулярных радиуса составляют угол в 90 0 и ограничивают 1/4 окружности.
Деление окружности на 4 и 8 одинаковых частей
Деление окружности на 3 и 6 равных частей (кратные 3 трём)
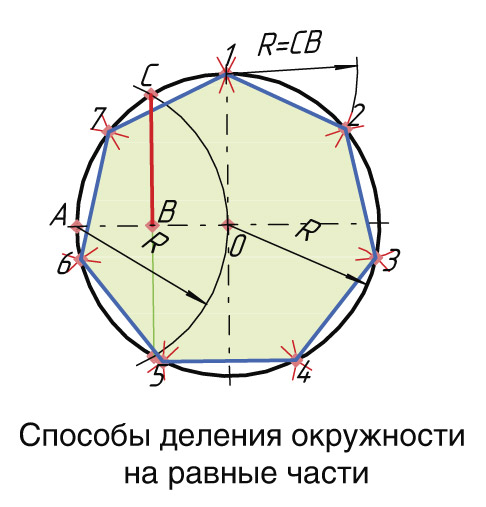
Для деления окружности на 3, 6 и кратное им количество частей, проводим окружность заданного радиуса и соответствующие оси. Деление можно начинать от точки пересечения горизонтальной или вертикальной оси с окружностью. Заданный радиус окружности последовательно откладывается 6-ть раз. Затем полученные точки на окружности последовательно соединяются прямыми линиями и образуют правильный вписанный шести-угольник. Соединение точек через одну даёт равносторонний треугольник, и деление окружности на три равные части.
Деление окружности на 5 и 10 равных частей
Построение правильного пятиугольника выполняется следующим образом. Проводим две взаимно перпендикулярные оси окружности равные диаметру окружности. Делим правую половину горизонтального диаметра пополам с помощью дуги R1. Из полученной точки «а» в середине этого отрезка радиусом R2 проводим дугу окружности до пересечения с горизонтальным диаметром в точке «b». Радиусом R3 из точки «1» проводят дугу окружности до пересечения с заданной окружностью (т.5) и получают сторону правильного пятиугольника. Расстояние «b-О» даёт сторону правильного десятиугольника.
Деление окружности на N-ное количество одинаковых частей (построение правильного многоугольника с N сторон)
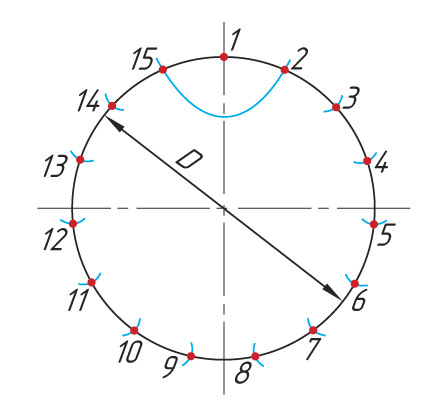
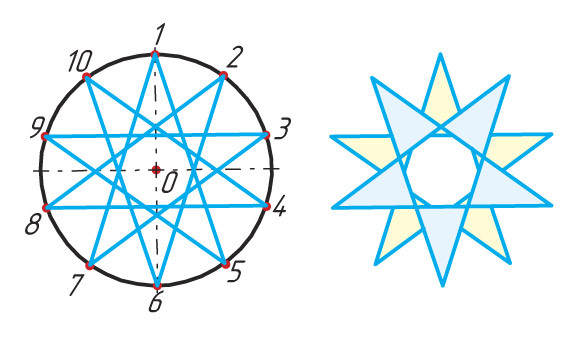
Выполняется следующим образом. Проводим горизонтальную и вертикальную взаимно перпендикулярные оси окружности. Из верхней точки «1» окружности проводим под произвольным углом к вертикальной оси прямую линию. На ней откладываем равные отрезки произвольной длины, число которых равно числу частей на которое мы делим данную окружность, например 9. Конец последнего отрезка соединяем с нижней точкой вертикального диаметра. Проводим линии, параллельные полученной, из концов отложенных отрезков до пересечения с вертикальным диаметром, разделив таким образом вертикальный диаметр данной окружности на заданное количество частей. Радиусом равным диаметру окружности, из нижней точки вертикальной оси проводим дугу MN до пересечения с продолжением горизонтальной оси окружности. Из точек M и N проводим лучи через чётные ( или нечётные) точки деления вертикального диаметра до пересечения с окружностью. Полученные отрезки окружности будут являться искомыми, т.к. точки 1, 2, …. 9 делят окружность на 9-ть ( N ) равных частей.
Нахождение центра дуги окружности
Для нахождения центра дуги окружности нужно выполнить следующие построения: на данной дуге отмечаем четыре произвольные точки А, В, С, D и соединяем их попарно хордами АВ и СD. Каждую из хорд при помощи циркуля делим пополам, получив, таким образом, перпендикуляр, проходящий через середину соответствующей хорды. Взаимное пересечение этих перпендикуляров даёт центр данной дуги и соответствующей ей окружности.
Черчение. 10 класс
§ 9. Деление окружности на равные части
Деление окружности на равные части
Для выполнения чертежей некоторых изделий необходимо овладеть приемами деления окружностей на равные части и построения многоугольников, вписанных в окружность (рис. 34, 35).
Деление окружности на 2 и 4 равные части. Любой диаметр делит окружность на две равные части. Два взаимно перпендикулярных диаметра делят ее на четыре равные части.

Последовательность деления окружности на 4 равные части
1. Проводят окружность с радиусом R.
2. Из точек С и В тем же радиусом R, что и радиус окружности, проводят дуги до их взаимного пересечения.
3. Точку пересечения соединяют прямой с центром окружности. Получают точки 1 и 3.
4. Аналогично выполняют построение из точек А и С.

Деление окружности на 3 и 6 равных частей
Последовательность деления окружности
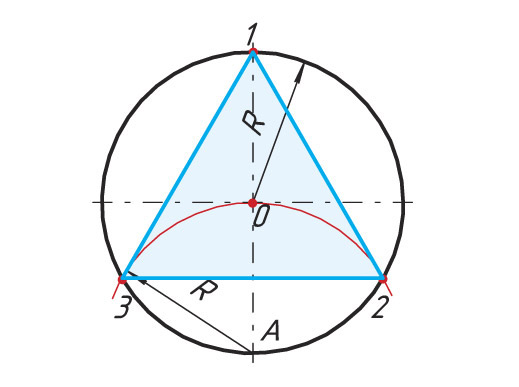
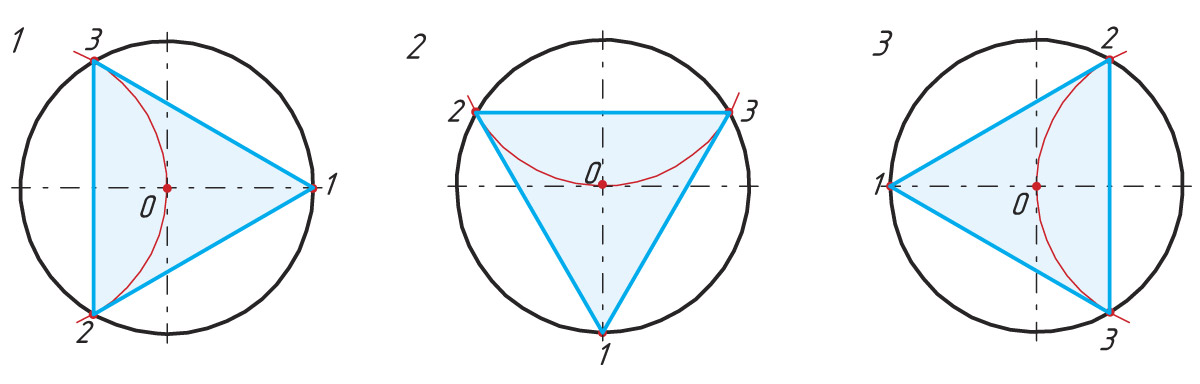
1. Проводят окружность с заданным радиусом R.
2. Из точки А тем же радиусом R проводят дугу до пересечения с окружностью в точках 2 и 3.
3. Точки пересечения 2 и 3 соединяют прямыми
линиями, получают вписанный треугольник.

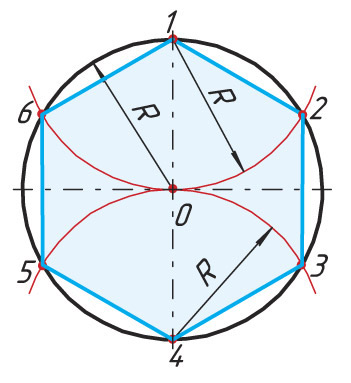
При делении окружности на 6 равных частей выполняется то же построение, что и при делении окружности на 3 части, но дугу описывают не один, а два раза, из точек 1 и 4 радиусом окруж ности R.
Выполнять деление окружности на равные части можно не только с помощью циркуля, но и используя угольник. Разделить окружность на число частей n можно, используя формулу расчета длины хорды (см. Памятку 4).
| Памятка 4. Деление окружности на равные части | |
| При помощи угольников | |
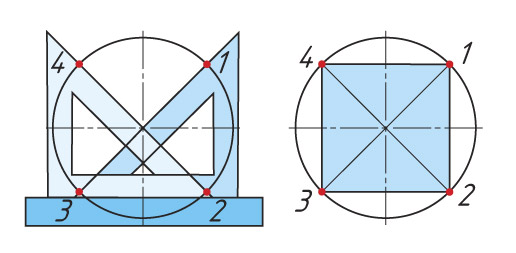 | 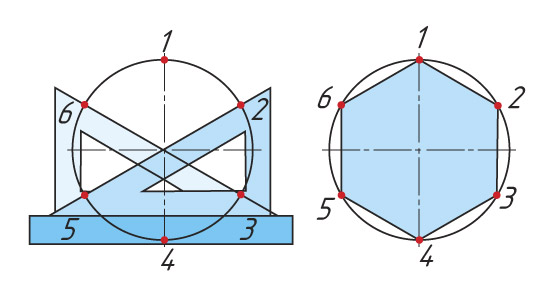 |
| Угольником с углом 45°. Гипотенуза угольника должна проходить через центр окружности | 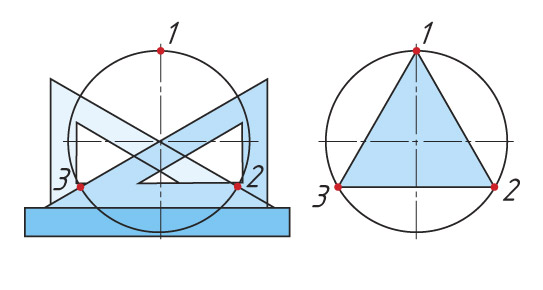 |
| Таблица коэффициентов для подсчета длины хорды | |
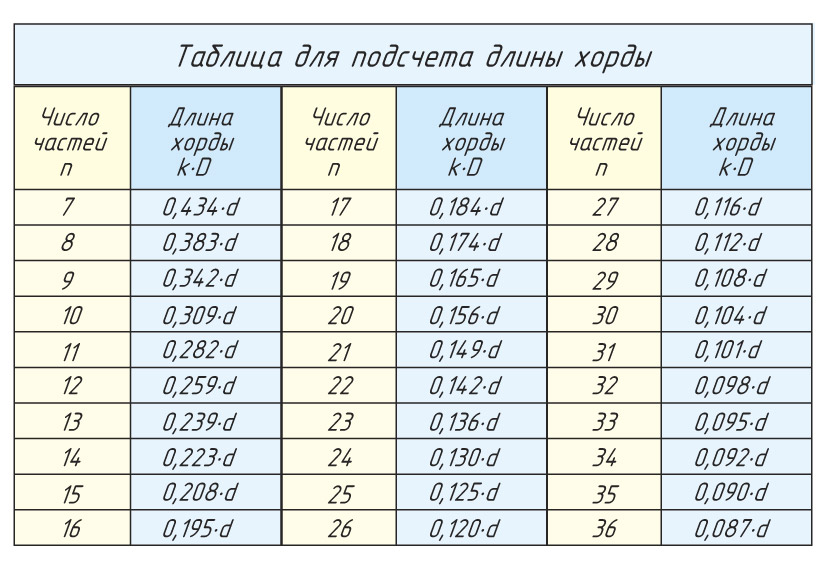 |  |







 Знаете ли вы, что не все кривые линии могут быть вычерчены с помощью циркуля и их построение выполняется по ряду точек? При вычерчивании кривой полученный ряд точек соединяют по лекалу, поэтому ее называют лекальной кривой линией. Точность построения лекальной кривой повышается с увеличением числа промежуточных точек на ее участке. К лекальным кривым относятся эллипс, парабола, гипербола, которые получаются в результате сечения кругового конуса плоскостью.
Знаете ли вы, что не все кривые линии могут быть вычерчены с помощью циркуля и их построение выполняется по ряду точек? При вычерчивании кривой полученный ряд точек соединяют по лекалу, поэтому ее называют лекальной кривой линией. Точность построения лекальной кривой повышается с увеличением числа промежуточных точек на ее участке. К лекальным кривым относятся эллипс, парабола, гипербола, которые получаются в результате сечения кругового конуса плоскостью. 